Monte Carlo方法与计算机模拟应用研究
2011-02-28魏丽英陈晓鹏
魏丽英,陈晓鹏
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.山西省潞安集团 地质处,山西 长治 046204)
模拟是指把某一现实的或抽象的系统的状态和特征,用另一个称为模型的系统来代替或模仿。电子计算机的出现及计算机科学技术的迅猛发展,给许多学科带来了巨大的影响。计算机不但使问题的求解变得更加方便、快捷和精确,而且使得解决实际问题的领域更加广泛。计算机适合于解决规模大、难以解析化以及不确定的数学模型,为系统模拟提供了极有力的工具。计算机模拟就是用计算机程序在计算机上模仿各种实际系统的运行过程,并通过计算了解系统随时间变化的行为或特性。
Monte Carlo方法,即随机模拟法,是用计算机模拟随机现象,通过仿真试验,得到实验数据,再进行分析推断,得到某些现象的规律或某些问题的求解的方法,它是计算机模拟的基础,它对解决随机性问题具有很强的能力。Monte Carlo方法的基本思想是:首先建立一个概率模型,使所求问题的解正好是该模型的参数或其他有关的特征量;然后通过模拟统计,即多次随机抽样实验,统计出某事件发生的频率。只要实验次数足够多,该频率便近似于事件发生的概率,这实际上就是概率的统计定义[1]。
Monte Carlo方法属于试验数学的一个分支,它研究的问题大致可分为两种类型,一种是问题本身是随机的;另一种是本身属于确定性问题,但可以建立它的解与特定随机变量或随机过程的数字特征或分布函数之间的联系,因而也可用随机模拟方法解决。本文旨在给出对Monte Carlo方法应用的一点思考,只涉及前一种问题。
1 Monte Carlo方法与Buffer问题
Monte Carlo方法源于1777年法国科学家Buffer提出的一种计算圆周率π的方法——随机投针法,即著名的 Buffer投针问题,其步骤为[1]:
(1)在纸上画出间距为d的平行直线;
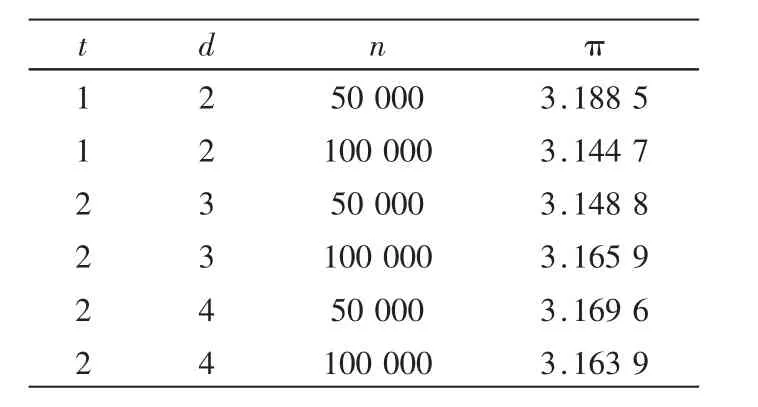
(2)取长度为t(t (4)计算出π的近似值。 可 令 x~U(0,d/2),θ~U(0,π), 建 立 直 角 坐 标 系(θ,x),如图2所示,由几何概率可知: 这里存在一个问题:算法的目的是计算π的值,而由此产生的模拟步骤中显然已利用了π的值(产生随机变量θ),这是矛盾的。笔者认为可直接将 sinθ当作一个随机变量,考虑用舍选抽样法来直接产生 sinθ,其中 θ~(0,π),其原理如下: 如图 3 所示,θ~U(0,π),在半圆周 D={(x,y)|x2+y2=1,y>0}上的每一个随机点与θ一一对应,故随机变量的抽样可由随机变量Y=(x,y)∈D的抽样代替,而随机变量sinθ的抽样可由Y中分量y的抽样代替,这是因为此时 改进后模拟步骤如下: (1)给定初值 t,d,n; 用Matlab编程实现,取ε=0.01时的统计结果如表1所示。 表1 计算机模拟统计结果 从表1可看出,运算精度与参数选取有很大关系,一个启示是实验模拟时要精心设置参数,并多次实验提高精度。 Monte Carlo方法可用来产生具有一定分布特征的随机数。 用 Matlab编程实现, 取 α=2,β=3,n=100,结果如表 2所示。 经检验其样本均值为0.400 0,样本方差为 0.043 0,而此Beta分布的期望是 0.4,方差是0.04,可见其模拟程度很好。 表2 Beta分布随机变量 表3 标准正态随机变量 (1)产生随机变量 ui~U(-3,3),vi~U(0,1); (2)检验 mf(ui)≥vi是否成立,若成立则令 xj=ui,j=j+1,否则转到步骤(1),直到i>n(n为预先给定的实验次数)。 用Matlab编程实现,取n=100,结果如表3所示。 经检验其样本均值为0.001 6,样本方差为0.914 5,可见其模拟程度较高。由标准正态随机变量,进行变换Y=μ+σX,可知 Y~N(μ,σ2),可得一般正态分布随机变量。 Monte Carlo方法是通过设计适当的随机试验而完成某种计算任务的方法,它对解决随机性问题具有很强的能力。随着电子计算机的高速发展,Monte Carlo方法在自然科学及社会科学领域的应用越来越广泛,许多用确定性方法难以解决的随机性问题都可以用它方便地解决,特别是在随机模拟方面更显示了其独特的魅力。Buffer问题反映了蒙特卡罗方法的思想,通过设计适当的随机试验来完成某种计算任务。但在利用计算机模拟随机试验时出现矛盾是由于Buffer问题本身不涉及常数π值,在利用计算机模拟试验中没有回避这一问题而造成的,因此应该设法避免[4]。 [1]重庆大学数学系.数学实验[M].北京:科学出版社,2000. [2]王梓坤.概率论基础及其应用[M].北京:北京师范大学出版社,2007. [3]杨肇夏.计算机模拟及其应用[M].北京:中国铁道出版社,1999. [4]左国新,陈应保.蒲丰问题与蒙特卡罗方法[J].高等函授学报(自然科学版),2005,18(2):3-4.

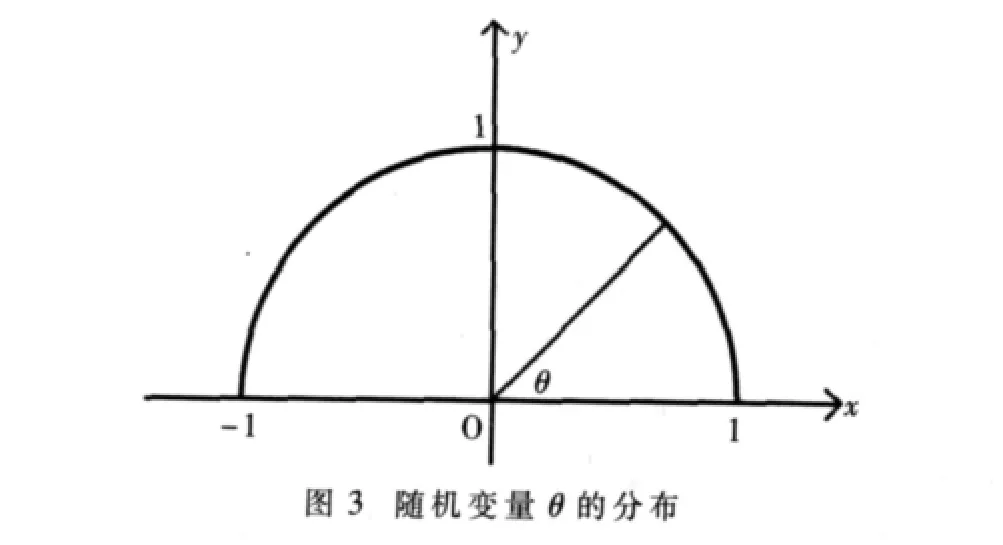

2 Monte Carlo方法模拟随机变量

2.1 Beta分布




2.2 标准正态分布


