图像中对数螺旋线的拟合
2011-02-28蒲平
蒲平
(暨南大学 计算机科学系,广东 广州 510632)
对数螺旋线(等角螺旋线)是一种在自然界中经常出现的曲线。由于它具有良好的几何、数学、力学及美学性质,使得它在计算几何、工业造型、天文及气象研究、动植物研究等现代学科中得到了广泛的应用[1]。
对数螺旋线是一条古老的曲线,很早以前人们就在几何上对它进行了一系列的理论研究。卫星云图中台风的形成路径可以近似看作为一条螺旋线,进而根据在图中提取的部分曲线段所进行的螺旋线拟合来确定台风中心[2]。银河星系中的涡旋星系图像中,旋臂结构所构成的形状近似为对数螺旋线。由于星系演化和旋臂结构之间的相互影响,通过研究旋臂结构可以了解星系的演化[3]。
由于对数螺旋线是一条非闭合的曲线,不能简单地按照传统的闭合曲线拟合算法来对其进行拟合。目前可以通过将对数螺旋线的极坐标方程 r=aebθ变换为 lnr=bθ+lna的形式,也就是把局部的对数螺旋线上各点的坐标通过在不同的极坐标系下进行变换使其成为能最佳地满足直线方程的形式,可以通过最小二乘法[4]或Hough变换[5]来求得该直线方程的系数,进而拟合出最佳逼近的对数螺旋线。
这些方法都是通过不断扫描图像中的每一个像素点来假设其为对数螺旋线极坐标方程中的原点(x0,y0),然后在以该点建立的极坐标系中根据图像中所获取的对数螺旋线上的点来求出极坐标系下的极半径和旋转角。由公式求出的旋转角也只能是在0~180°的范围。而实际给出的对数螺旋线的旋转角度可以大于360°。
本文通过缩小极坐标原点的遍历区域来减少运算次数,达到提高运算效率的目的。同时考虑所获得弧段的极角大小在任意范围内。
1 对数螺旋线的拟合
1.1 对数螺旋线的主要性质
对数螺旋线的极坐标方程为:

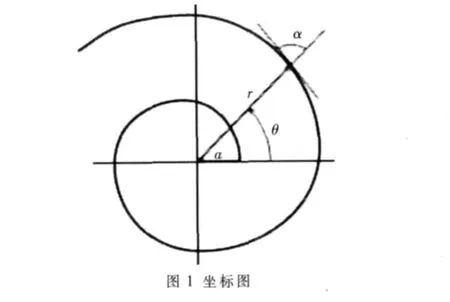
其中,θ为极角,r(θ)为极径,α为极径与切线间的夹角,如图1所示。
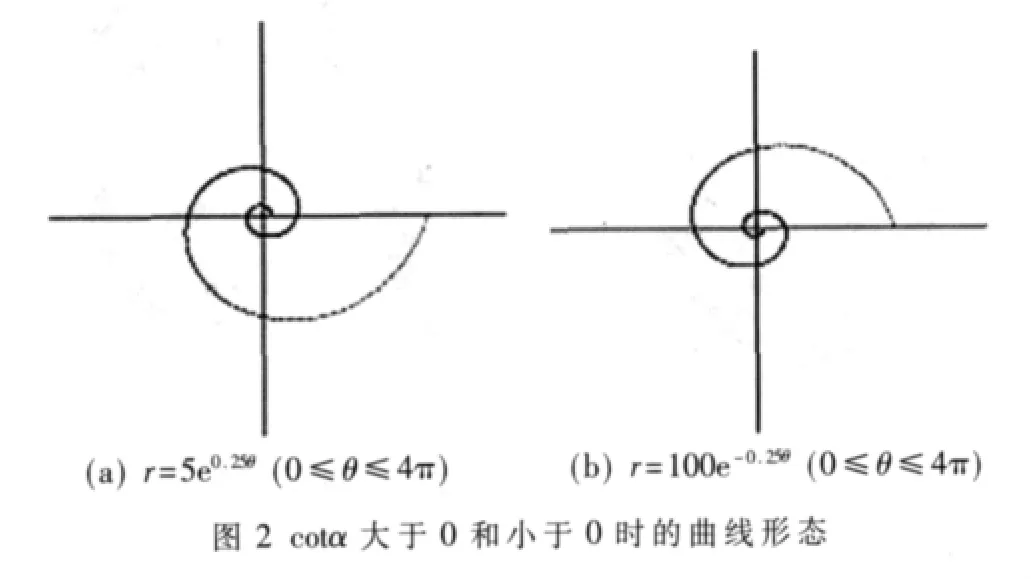
根据式(1)可以看出,对每个θ值,都有一个对应的r值,而且不同的 θ值所对应的 r值也不同 (因为 cotα≠0)。这种现象表示:从对数螺旋线上某个点出发,随着θ值的无限增大与无限减小,此曲线会环绕它的极点形成无数多圈,一面是越绕越远,一面是越绕越聚集在极点附近。若 cotα>0,则当 θ→-∞ 时,曲线聚集在极点附近;若 cotα<0,则当 θ→-∞ 时,曲线越绕越远,如图 2所示。
等角螺线上的一段弧经伸缩若干倍后,必与该等角螺线上的另一弧全等。事实上,若对数螺旋线r=aeθcotα伸缩 成 r=ae(θ+φ)cotα,则 在 对 数 螺 旋 线 r=aeθcotα上 ,极 角 θ满 足β≤θ≤γ的弧,经伸缩后必与该等角螺线上极角θ满足β+φ≤θ≤γ+φ的弧全等。对数螺旋线的这项特性使得自然界中许多物体都呈现对数螺旋线的形状。例如许多贝壳都很接近对数螺旋线的形状,因为生活在壳内的动物在成长过程中都是均匀地长大的,这就像相似地放大,所以,新生的部分所栖息的空间必与原有空间形状相似。象鼻、动物的角与毛等都呈对数螺旋线形。
1.2 坐标变换
将参数方程 r=aebθ两边同时取对数,得到:lnr=bθ+lna。可以将该式看作是关于θ和lnr的直线形式。由于从已知图像中获得的数据点的坐标为直角坐标系下的值,即需将直角坐标系下的点(x,y)变换到(θ,lnr)坐标系下。
选取图像中任意一点(x0,y0)为极坐标原点建立新的极坐标系。根据在图像中获取的一系列数据点(xi,yi)(i=1,2,…,k),通 过 式(2)、 式(3)可 将 其 转 换 为(θi,lnri)(i=1,2,…,k)形式的数据点。


1.3 对数螺旋线中心点的取值范围
由于处理过程中需要得到r和θ的值,而它们需要在极坐标系下获取,图像中的任意一点(xi,yi)在选择不同的极坐标原点所建立的极坐标系下所获得r和θ的值也不相同。由于给定图像中并不知道该曲线的极坐标原点,故常用的方法是假设极坐标原点存在于该幅图像中,进而通过对整幅图像进行扫描来寻找该点。但这需要遍历整个图像,效率十分低下。
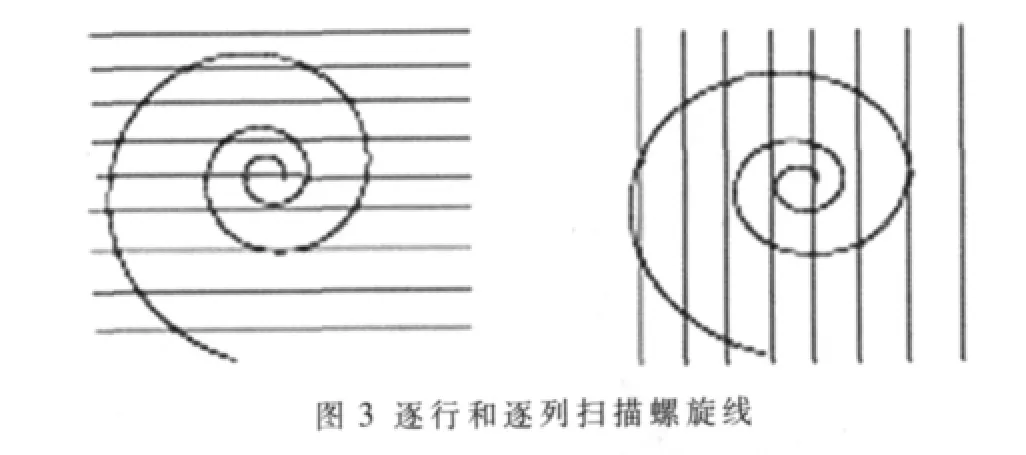
由对数螺旋线的每一个性质可知,该曲线由内到外逐渐发散或者是由外到内逐渐聚集在极点附近。对于超过一圈的螺旋线而言,可以通过逐行与逐列地对整幅图像进行扫描,判断扫描直线与图像中螺旋线的交点个数,如图3所示。可以发现越靠近螺旋线的中心其交点个数越多。分别在水平和竖直方向上统计其交点的个数,通过设定一定的误差范围可以获得一个交点个数较大的区间。由于在水平和竖直方向上都能获得一个区间,从而可以获得一个包含中心点的矩形区域。则中心点的选取可以缩小到该区域来进行遍历。
1.4 旋转角的获取
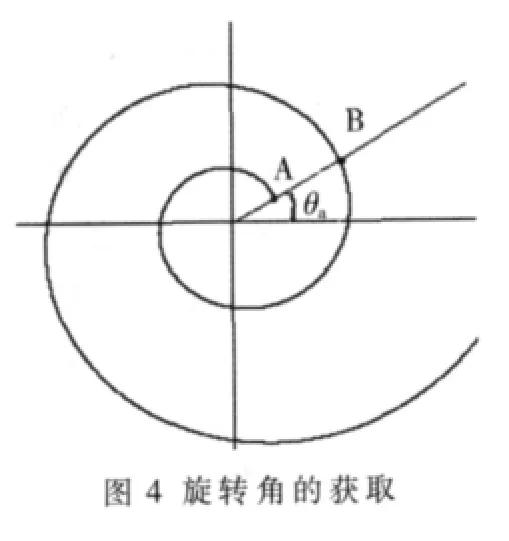
对数螺旋线是一条非闭合的曲线,它能包含多圈。如图4所示,点A和点B由式(2)可以得到不同的极径值 r。由式(3)求得的极角的值相同,但是正确的应该是如果点A的极角大小为 θa时,点 B的极角大小应该为(360°+θa)。
对于具有多圈并且曲线中只含有两个端点的对数螺旋线,假设起始端点的极角为θ1,则沿着曲线进行跟踪,由式(3)得到的极角值的变化趋势应该为从 θ1递增到360°,接着再从 0°递增到 360°直到终点。可以发现每当极角的值从 360°变为 0°时则刚好走完一圈,则刚好需要增加 360°。
通过上述分析可以得出,当获得的极角值前后两个数据剧烈递减且二者之差为一个较大的正数时,需要增加 360°,即 θi=(θ1+360k)(k=1,2,…)。
1.5 最小二乘拟合
由上面的分析可知,对于要搜索的每一个极坐标原点(x0,y
0)都能由已知图像中获得的点经变换而得到一系列数据点(θi,lnri)。通过这些点由最小二乘法[5]可以求出直线的参数b和lna。根据误差公式可以求出对于每个极坐标原点所对应的误差值大小,满足误差最小的直线参数即为所求。
2 实验与分析
为验证本文方法的有效性,分别采用仿真图像及真实图像对算法进行测试。实验环境:CPU主频为2.80 GHz,内存为256 MB。实验结果如图5所示。

图5(a)为具有多圈的对数螺旋线人工仿真图。图5(b)是对原图细化到单像素宽度[6],分别找出起始点和终点。图5(c)为分别从水平方向和竖直方向对图像进行扫描统计的交点个数。图5(d)为在水平和竖直方向上获得的交点个数较多的区域。图5(e)为通过遍历由图5(d)获得的区域内每一像素点并以其为极坐标原点建立极坐标系,将原图像中数据点变换为该坐标系下,通过最小二乘拟合后求出的误差最小的曲线。该方法耗时为2.111 s,如果在整个图像中遍历寻找极坐标原点,则需要耗时58.467 s。
表1给出了对数螺旋线的原始数据和拟合后的参数,其中(x0,y0)为中心点坐标,a和b分别为对数螺旋线中的参数值。由表1可知,拟合出的对数螺旋线与原始图中心点相同,参数a和b值基本一致。
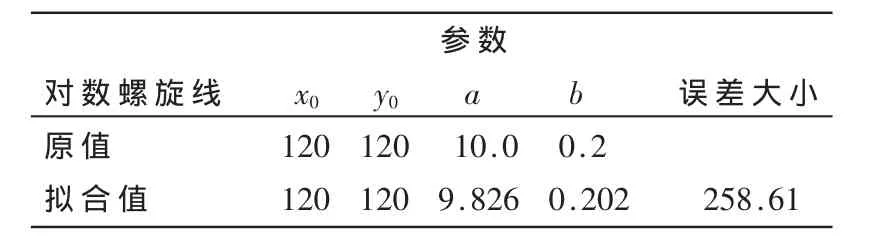
表1 人工仿真对数螺旋线拟合结果
图6描述了对台风所形成的卫星云图进行处理的结果。图6(a)为真实卫星云图,图中含有螺旋云带。图6(b)为提取原始图像中的部分区域。图6(c)为使用otsu方法得到的二值化图像。图6(d)为将二值化图像通过形态学方法(膨胀和腐蚀等)将图像中的螺旋云带进行独立的分割所得到的图像。图6(e)为通过面积分割提取出来的螺旋云带。图6(f)为将螺旋云带中的空洞去掉后的结果。图6(g)为对图像进行细化后的结果。图6(h)为通过找出曲线中的各个端点,提取出曲线中最长的一条曲线段,以此来对细化后的图像去掉毛刺。图6(i)为对提取出来的曲线段进行样条平滑后的结果。图6(j)为分别在水平和竖直方向上进行扫描统计出的交点个数。图6(k)为找出统计的交点个数较多的相交区域。图6(m)和图6(n)为用最小二乘法对其进行拟合后的结果。

本文通过约束对数螺旋线中心点的存在范围,将对数螺旋线的拟合转换为直线的拟合。实验结果表明,本文方法能够快速、较为准确地拟合出图像中存在的对数螺旋线。然而实际中,包含不同螺旋线的图像需要具体地分析,寻找更为合理有效的方法。
[1]游世辉,李军.对数螺线的应用研究[J].九江学院学报(自然科学版),2005(3):6-9.
[2]谢俊元,艾早阳.台风中心定位中的螺旋线自动识别算法[J].软件学报,1997,6(增刊):398-403.
[3]FRUHWIRTH R,STRANDLIE A.Helix fitting by an extended riemann fit[J].Nuclear Instruments and Methods in Physics Research(A),2002,490(1-2):366-378.
[4]刘凯,黄峰.无眼台风自动定位方法研究[J].信息与控制,2001,30(6):543-546.
[5]孔秀梅.形成期台风螺旋云带的提取、描述及中心定位的研究[D].天津:天津大学,2003.
[6]STEFANELL R,ROSENFELD A.Some parallel thinning algorithms for digital pictures[J].Journal of ACM,1971,18(2):255-264. (收稿日期:2011-02-28)
