一种基于SIFT和SUSAN特征的图像匹配方法
2011-02-28吴毅良
吴毅良
(暨南大学 计算机科学系,广东 广州 510632)
图像匹配是图像处理的一个基本问题,在计算机视觉、图像配准、信息检索等领域得到了广泛的应用,是很多基于图像内容应用的基础。随着计算机技术的发展和数字图像应用的日益广泛,图像匹配技术在诸多领域内发挥越来越重要的作用。长期以来,国内外很多学者都致力于解决图像匹配的技术问题。
简单来说,图像匹配就是找出两幅图像中相同或相似景物,目前图像匹配的方法一般分为基于区域匹配和基于特征匹配两类。
近年来,在计算机视觉领域,基于局部不变量描述符的方法在目标识别和图像匹配方面取得了显著发展。SIFT特征描述符克服了传统图像匹配在图像尺度、视差变化的局限性。参考文献[1]对10种最具代表性的特征匹配描述算子进行了实验和性能比较,结果表明,SIFT特征描述符在对光照变化、图像旋转、比例缩放、几何变形、模糊和图像压缩等6种情况下性能最好。
本文在SIFT方法的基础上加入SUSAN角点检测的思想,提出一种新的更加稳健的图像匹配方法。
1 SIFT特征检测
2004年,LOWE D提出了一种新的点特征匹配算法——SIFT(Scale Invariant Feature Transform)算法,较好地解决了场景部分遮挡、旋转缩放、视点变化引起的图像变形等问题,并且有效应用于目标识别、图像复原、图像拼接等领域。
SIFT算法首先在尺度空间进行特征点检测,并确定关键点的位置和所处的尺度,然后使用关键点邻域梯度的主方向作为该点的方向特征,以实现算子对尺度和方向的无关性。
1.1 尺度空间理论
尺度空间理论是一种对图像从多尺度考察图像特征的理论方法,能够发掘出很多从单一尺度无法发现的图像特征。
SIFT方法选用了高斯函数,利用其标准差σ作为尺度参数与图像进行卷积运算以产生多尺度的图像。一幅二维图像的尺度空间定义为:

其中*表示卷积,G(x,y,σ)是尺度可变高斯函数,

其中(x,y)是图像的二维坐标,σ是尺度坐标。
σ称为尺度空间参数,其值越小表示图像被平滑得越少。大尺度对应图像的概貌,小尺度对应图像的细节。给定一个σ,就决定了一个高斯滤波器,以不同的σ对原图像进行滤波就可以生成对应的尺度空间图像。
由式(1)可以看出,高斯卷积需要利用一个二维可变大小的卷积模板进行运算,运算效率低下。本文将式(1)分解成分别对x方向和y方向作一维卷积,将二维高斯模糊转变成两次一维高斯模糊,大大减少了运算时间。
SIFT实际是使用DoG算子来建立尺度空间,它是LoG算子的近似,具有很好的稳定性,且比LoG运算更加高效。DoG定义如下:
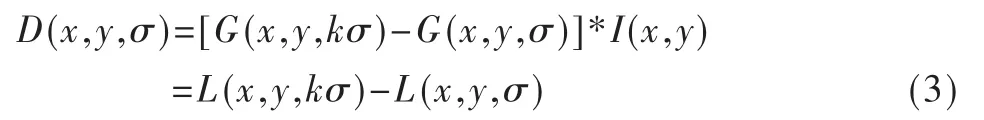
由式(3)可知,DoG其实就是利用两个临近尺度的高斯滤波图像相减得出的,因此计算量上只是增加了一次减法运算。
1.2 检测空间极值点
生成尺度空间后,需要检测空间上的极值点,同时对同一尺度的周围邻域8个像素和上下相邻尺度对应位置的邻域9个像素,一共26个像素进行比较,如果当前像素比周围26个像素都大或者都小,就认为该点属于极值点。
1.3 精确定位极值点
因为DoG算子具有比较强的边缘响应,在边缘上可能会产生不稳定的特征点,所以有必要把这些不稳定点去掉,以增强匹配稳定性,提高抗噪声能力。本文通过拟和尺度空间的三维二次函数可以精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点。
1.4 计算方向参数
利用极值点邻域像素的梯度方向分布特性为每个极值点指定方向参数,使算子具备旋转不变性。

其中θ和m为(x,y)梯度的方向和模。
1.5 特征描述子
首先以特征点为中心取8×8的邻域作为采样窗口,窗口内每个方格代表特征点尺度空间的一个像素,箭头方向代表该像素的梯度相对于特征点方向的相对方向,箭头长度代表梯度的模,大圆圈代表加权的范围。然后利用直方图统计的方法,在每 4×4的小块上计算 8个方向的梯度方向直方图,即可形成 4个种子点,如图1所示。

每个种子点可以产生8个方向信息,共4×8=32个方向信息,按顺序就可以组成32维的特征向量。本文采用16×16的采样窗口,一共产生 16个种子点,产生16×8=128维的特征向量,更多的种子点可以增加匹配的稳定性。
2 SUSAN角点检测
1997年 SMITH S M和 BRADY J M提出了一种最小核值相似区SUSAN(Smallest Univalue Segment Assimilating Nucleus)算法,它直接对图像灰度值进行操作,方法简单,算法效率高,定位准确,对多个区域的角点也能精确检测,对局部噪声不敏感,抗噪能力强。
2.1 SUSAN方法简介
SUSAN方法其实是利用圆形模板遍历整个图像,如果模板内其他像素值与模板中心像素值相差小于一定阈值,就认为该点与中心点具有近似的灰度值,模板内满足这样条件的像素组成的区域称为核值相似区USAN(Univalue Segment Assimilating Nucleus)。利用这个区域可以将像素点的性质分成几类考虑,而属于直角角点的大概就是具有1/4模板大小的USAN区的像素点,如图2所示。

2.2 USAN区域
USAN区域利用中心点与周围像素的差值和预先设定的阈值进行比较得出,其相似比较函数表示为:

2.3 角点检测
SUSAN方法通过设定角点阈值,利用角点响应函数判断角点位置,计算公式如下:

其中g为角点阈值,它影响检测到的角点形状,g越小,检测到的角点越尖锐,一般设定为1/2模板区域大小。
SUSAN角点检测的最后一个阶段,就是寻找初始角点响应的局部最大值,在局部范围内,如果中心像素的初始响应是此区域内的最大值,则判断其属于角点。
3 基于SIFT和SUSAN特征检测
SIFT方法能够从尺度空间寻找出具有结构化特性的特征点,但是可能在视觉上没有特殊意义,而实际图像中很多具有视觉意义的特征位置,如角点利用SIFT方法检测会出现位置偏移或者漏检的情况,如图3所示。

从图3可以看出,最右角出现漏检,其他角的特征点均发生一定程度的位置偏移,这是由于高斯平滑的过程中极值点会随着像素扩散引起的。但是图像上的角点往往是进行图像匹配比较理想的特征,SIFT方法并没有很好地将角点利用起来,遗漏了某些重要的角点信息。
本文在SIFT的基础上引入SUSAN角点检测就是为了增强其对图像特性信息的利用率,从而应用于图像匹配上得到更多有意义的正确匹配点,因为SUSAN能够有效检测出图像中的角点,如图4所示。
由图4可以看出,SUSAN方法能够准确定位并检测到4个角点。SUSAN角点检测的优点在于可以简单快捷地检测出图像的明显形状特征,但是针对纹理图像或者低对比度图像,效果并不明显。
通过以上分析,本文在SIFT方法的基础上引入SUSAN角点检测思想,基本能够将图像中的结构化信息特征和形状信息的特征检测出来。算法的流程图如图5所示。


图5 算法流程图
4 特征匹配
已经找出图像上的特征向量,接下来的任务就是特征匹配,即对特征向量作相似性度量判断其相似程度。本文采用两个向量的欧氏距离作为相似性的判断度量,欧氏距离定义如下:

取图像1中的某个关键点,并找出其与图像2中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离小于某个比例阈值,则接受这一对匹配点。如果降低这个比例阈值,匹配点数目会减少,但更加稳定。最后再设定一个匹配点数目阈值,如果匹配点数目大于阈值,就认为两幅图像是相似的。
5 实验结论
在Core 2,2.2 GHz CPU,2.0 GB RAM的PC机上运行Solaris 10操作系统,采用C语言编程实现了本文提出的算法,通过实验图片验证本文方法的有效性(限于篇幅,下文仅给出一组实验结果),并将本文算法与SIFT算法进行了实验分析和比较。实验中,最近邻特征点距离与次近邻特征点距离之比取0.7。

图6利用SIFT方法,左图和右图分别生成了356个和369个特征点,最终产生12对匹配对,其中两个错误的绝对变化在0.01以内,相对变化在1%以内。理论上来说,k取值越大,相邻模型变化就越小,极限情况下,模型应该收敛到一个统一模型,这种极限模型称为稳定模型。一个网格划分对应一个稳定模型。从图6和表1可以看出,k取任何值,所得模型都很接近该网格划分对应的稳定模型,考虑到k取1时所得模型不够光滑,因此,认为k取2所得到模型很接近稳定模型。由此可以看出,在计算PSF模型时,网格的细密程度对计算模型的准确性影响很大,当网格划分固定后,只要保证每网格内有两个采样数据就可以得到稳定的模型。总体来说,采样星体数目达到2n2个就可以得到较好的稳定模型。
本文通过对模拟欠采样星象的处理实验,可知处理欠采样星象使用ePSF方法计算PSF模型时,每个网格的采样星体越多,计算结果越逼近一个稳定模型,这个稳定模型和真实模型的误差主要由网格划分的细密程度来决定,网格划分越密,模型误差越小。当网格划分固定时,每网格内有两个采样数据时即可得到一个较精确的稳定模型,即采样星体数目对ePSF网格模型的准确性影响不大。但在实际处理中,由于星体的相位差分布不均,因此平均每网格采样星体数目应该大于2。该结论在实际应用ePSF方法时,对更精确的建模有一定的指导意义。
[1]ANDERSON J,KING I R.Toward high-precision astrometry with WFPC2.I.Deriving an Accurate Point-Spread Function[J].PASP,2000,112:1360-1392.
[2]ANDERSON J,BEDIN L R,PIOTTO G,et al.Groundbased CCD astrometrywith wide field images I.Oberservations just a few years apart allow decontamination of field objects from members in two globular clusters[J].A&A,2006,454:1029-1045.
[3]张志渊,彭青玉.ePSF拟合法与Gaussian拟合法的比较[J].Astronomical Research&Technology,2010,7(2):132-139
[4]KING I R.The profile of a star image[J].PASP,1971,83:199-201.
[5]李展,彭青玉,韩国强.CCD图像数字定心算法的比较[J].天文学报,2009,50(3):340-348.
