时域模态参数识别在南京长江大桥安全监测中的应用

郭 鑫,黄方林

(湖南省交通规划勘察设计院,湖南长沙 410008)

0 引言

南京长江大桥是我国自行设计建造的首座特大铁路、公路两用钢桁梁桥。江面正桥1 576 m。该桥位于我国铁路南北通道京沪干线和公路干线宁杨国道上,是我国华东地区乃至全国发展国民经济的重要交通命脉。全桥于1968年底通车,至今已经安全运营了42 a,但某些部位已经出现轻微病害。即将建立的南京长江大桥安全监测与状态评估监测系统,将对桥梁的结构响应与行为以及桥梁工作环境进行实时监测,并利用获取的信息分析结构的健康状态、评估结构的可靠性,为桥梁管理与维护提供科学的决策依据。桥梁安全监测和状态评估系统作为一多学科交叉的综合体系,其理论覆盖到振动理论、测试技术、系统辨识理论、信号分析与处理技术、计算机技术、可靠度等多门学科。从国内外应用的实例来看,目前普遍采用实验模态分析方法来进行结构安全监测和状态评估,因为它具有较好的在线性、遥感性和提取信号的方便性,而且由实测数据经分析得到的模态参数,像固有频率、阻尼比、振型等都是反映结构整体性能的可靠“指纹”,可作为评价大桥整体性能的重要依据之一[1]。模态参数识别的方法有频域法和时域法,其中频域法相对较成熟,是模态参数识别的主要方法,常见的频域法有半功率带宽法、峰值法、导纳圆法等方法[2]。但它的实验设备较复杂,试验周期也较长,特别是在对大型结构中的激振力无法测量时,用时域法进行模态参数识别的优点明显。时域识别的方法很多,常用的有复指数法、对数衰减率法、ITD法[3]、STD法[4]、随机减量法[5,6]等。本文介绍的是一种时域识别方法——逐步扩阶双递推法[2]。逐步扩阶双递推法是利用自由振动响应(或脉冲响应函数)识别系统复模态参数的时域参数识别法,它可克服复指数法判阶困难的缺点。此外为了节省计算机机时和内存,采用了最小二乘递推和逐步扩阶的双递推法,提高了识别效率和精度。利用该法进行仿真计算和对南京桥实测数据分析,结果是令人满意的。

1 理论背景

式中[M]、[C]、[K]分别为系统质量矩阵、阻尼矩阵、刚度矩阵,{x}、◦x、 {◦◦x}分别为用物理坐标描述的位移列阵、速度列阵、加速度列阵。考虑第k个测量点,它的自由响应表达式可表为:

一N自由度线性系统自由振动微分方程:

现以采样周期Ts对xk(t)进行采样,记tj=jTs,简记为j(j=0,1,2,…),zi=eλiTs,则有:

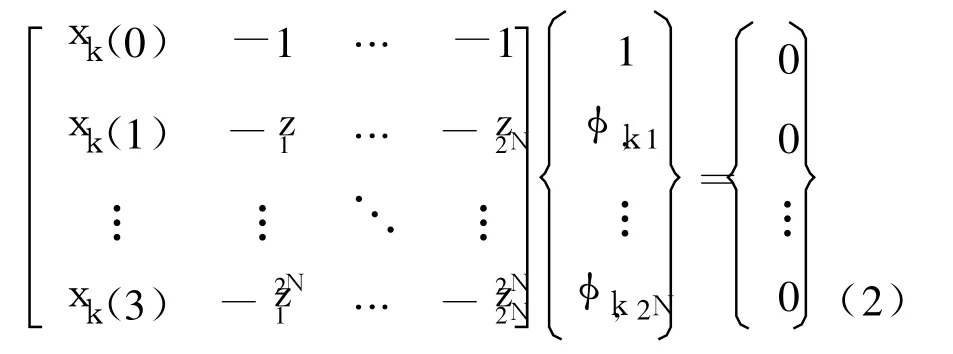
式c1,c2,…,c2N为自回归系数。以zj代替式(2)中系数矩阵相应行列式的第一列xk(j)(j=0,1,…,2N),则当z=zi时,行列式的第一列与i+1列成比例,式(3)仍成立,故得:

将式(4)时延得最小二乘解:

式中θr=(c1,c2,…,c2N)T;Rr=(-xk(1,0),-xk(2,0),…,-xk(r,0))T;Φr为θr的系数矩阵。求得c1,c2,…,c2N,解式(4),可得zi及复频率λi。

利用一个测量点的自由振动响应数据,且作时延,构成Φr、Rr。式(5)中的Φr、Rr均为r行,用r行(即r个方程)由该式获得的解记为θr、Φr、Rr,每增加一行(即增加一个方程),分别记为0),则可利用θr、及0)导得θr+1的最小二乘递推公式:

其中初始值P0、θ0,在此可直接令P0=c2I,θ0=0,是计算机允许的充分大的数。

为了考虑测量噪声的影响,让噪声模态有出口,假定响应中包含了N阶复模态。利用低阶的估计值θ,用递推算法求得扩阶后的θ*。令:

则与Φr相应的矩阵记为:

高校图书馆作为学术科研获取信息资源的重要渠道，致力于OA学术资源的收录、揭示、组织、管理等方面的研究与实践，基本形成了资源收录类型全、学科范围广、质量水平高、揭示角度多、揭示方式明确、组织方式科学、宣传渠道多样的整体局面，OA学术资源得到了较为广泛的利用与传播。

式中Φ1即为式(5)中模型阶为i时的Φr。于是有:

解上式得:

式中:

由式(8)可知,可根据i阶模型的估计值θ,以及Φ1,Φ2,R可迅速算得扩阶后得估计值θⅠ、θⅡ。矩阵B2的求逆仅仅是一个二阶矩阵的求逆,比较方便。而矩阵C2的求逆可采用分块矩阵求逆法。于是,我们就得到了一组逐步扩阶双递推公式(6)、式(9)。具体步骤是:首先任意确定一个较小的拟合模型阶i,按式(6)进行最小二乘递推,推到第r个方程时得估计值θr,如需进行扩阶,这时令C2=Pr、θ=θr,按式(9)进行扩阶递推,如有必要可增加新的方程,利用式(6)进行递推,这时式(9)中的Pr=Cr,θr={θⅠ:θⅡ}T。由此可知,最小二乘递推与逐步扩阶递推的组合,提供了方便、灵活的参数识别手段。

逐步扩阶双递推法是利用自由振动响应(或脉冲响应函数)识别系统复模态参数。如果得到的数据是平稳随机响应(如地脉动响应),可以通过随机减量法[2]从线性振动系统的一个或多个平稳随机响应样本函数获得该系统自由振动响应的数据。

2 仿真计算及实测结果验证

2.1 仿真计算

考虑一个4自由度系统,其测量点1的自由响应为:

式中:

ω1=10 rad/s;ω2=40 rad/s;ω3=90 rad/s;ω4=160 rad/s;σ1=σ2=σ3=σ4=1.00;Ψ=[1 2 3 4]T。

为模拟测量噪声,在x1(t)中分别添加10%,15%,20%的随机白噪声,用逐步扩阶双递推最小二乘法进行识别,其结果见表1。

表1 仿真结果比较

仿真结果表明,在噪声水平越低的情况下,识别模态参数精度越高。ψ中数值越大,对应阶次的模态参数识别结果越好。

2.2 实测结果分析

利用CA—YD型加速度传感器、DH5935放大器和便携式计算机对南京长江大桥的响应进行了测量。测点主要布置在南京联的主桁杆件、纵梁和横梁上,采样频率为500Hz,记录了大桥在上、下行各种客、货列车通过时和无列车通过时的加速度响应。实测的南京联中跨中截面的下弦杆竖向加速度响应(包括低通滤波后)及其自功率谱如图1所示。

现截取一个测点的列车通过后余振数据,其竖向加速度响应(包括低通滤波后)及自功率谱如图2～图5所示。

图1 实测大桥的加速度响应和频谱曲线

图2 滤波前的测点余振响应

图3 滤波后的测点余振响应

图4 低通滤波前功率谱图

图5 低通滤波后功率谱图

通过逐步扩阶双递推最小二乘法计算得到结果:

1)滤波前得到固有频率:2.225、4.679 4、5.388、9.941 3 Hz,对应阻尼比分别是:0.007 1、0.003 0、0.006 5、0.006 6。

2)低通滤波后得到固有频率:2.230 3 Hz,阻尼比:0.013 6。

通过ANSYS软件对南京桥动态分析得到的前10阶固有频率如表2所示。可知余振响应中第二阶模态占主要成分。

表2 理论计算的前10阶固有频率

3 结论

模态参数作为反映整体结构动力特性的可靠“指纹”,在大型复杂结构的安全监测中起着重要的作用。为识别南京长江大桥模态参数,且不影响其正常运营,时域识别是非常适用的。

本文介绍的逐步扩阶双递推最小二乘法及其与随机减量法的综合运用可对火车过桥、过桥后的余振、地脉动等各种情况下由测量到的响应进行模态参数识别。仿真与实测数据分析结果表明该方法应用于南京长江大桥安全监测是可行的。

[1]何旭辉,陈政清,黄方林.南京长江大桥安全监测和状态评估的初步研究[Z].

[2]周传荣,赵淳生.机械振动参数识别及其应用[M].北京:科学出版社,1989.

[3]Ibrahim SR,Mikulcik EC.Amethod for the direct identification of vibration[J].Shocked Vibration Bulletin,Part 4,1997.

[4]Ibrahim SR.An approach for reducing computational requirements in modal identification[J].AIAA Journal,1986,24(10).

[5]Ibrahim SR.Random decrement technique formodal identification of structures[J].J.of Spacecraft and Rockets,1977,14(11).

[6]黄方林,何旭辉,陈政清,等.随机减量法在斜拉桥拉索模态参数识别中的应用[J].机械强度,2002,24(3).

[7]Huang Fanglin,He Xunhui,et al.Health Monitoring for Nanjing Yangtse River Bridge[Z].Proc of the 7th Int.Symposium on structural Engr.for young experts,Tianjing,2002.

[8]刘君辉,宋友成.大跨度桥梁施工过程中参数识别的BP神经网络方法[J].湖南交通科技,2003,29(2):49-51.

[9]虢曙安.连续刚构桥施工控制中的参数识别方法研究[J].公路工程,2009,34(3):135-137.

[10]郭木华.基于二分法的斜拉桥施工控制过程参数识别[J].公路工程,2010,35(3):132-135.

[11]张治国,张谢东.基于模态分析理论和神经网络的斜拉桥拉索损伤识别研究[J].中南公路工程,2007,32(2):67-72.

[12]喻力斌.杨梅昌江大桥T梁安全架设方案的实施[J].中南公路工程,2005,30(2):130-131.