水中结构的动力响应分析＊

雷 凡 杨吉新 刘 惠 方 伟

(武汉理工大学交通学院1) 武汉 430063) (湖北鄂东长江公路大桥有限公司2) 黄石 430030)

0 引 言

近年来各国越来越重视海洋资源的开发与利用,相继建造了许多诸如跨海大桥、海洋平台、海底油气管道、海底隧道、超大型浮体等海洋工程结构.这类结构容易在波、流、地震等外部荷载的作用下产生有害振动,严重时可产生疲劳破坏[1-2].而且其施工难度大,养护维修费用高,因此,研究水中结构在动荷载作用下的响应十分重要.

当水流垂直流经钝体结构时,在一定的条件下,结构两侧会周期性地发生漩涡泄放现象,从而产生作用在结构上的周期性交变荷载.当涡泄频率接近于结构的自振频率时,结构与流体之间的耦合效应变得十分显著,将发生垂直于流向的强烈共振现象[3-4].本文将海洋悬跨管道、悬浮隧道等两端约束的结构简化为简支梁模型,将漩涡泄放产生的升力简化为简谐荷载,考虑流固耦合作用,分析水中结构的动力响应.

1 水中结构的运动方程

在建立水中结构的运动方程时,常使用附加质量法代替水对结构的作用.为进行分析,引入如下假设：(1)结构为两端简支的 Euler-Bernoulli梁,考虑其弯曲刚度;(2)结构为圆形截面,其几何尺寸、刚度和材料性质沿长度方向不变;(3)海流为均匀定常流,且流向垂直于梁的轴线.

令系统坐标原点为梁左端截面中心处,x轴方向与梁轴线重合,在上述假定条件下,水中结构在涡激升力作用下的运动方程可表示为

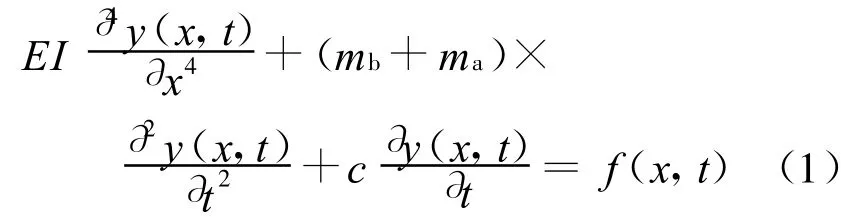
常用的涡激升力 f(x,t)表达式为[6]

式中：CL为升力系数;V为流体流速;ωs为涡泄频率.

由涡激升力的表达式可以看出,在流体速度恒定的情况下,作用于结构的涡激升力为固定振幅的简谐荷载,可表示为

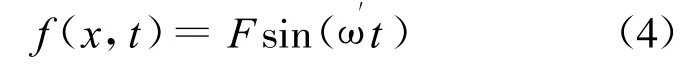
使用分离变量法,令

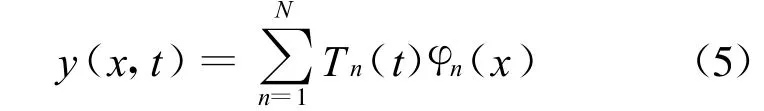
式中：Tn(t)为t时刻第n阶模态响应;φn(x)为第n阶模态函数,均匀简支梁的固有频率为[7]

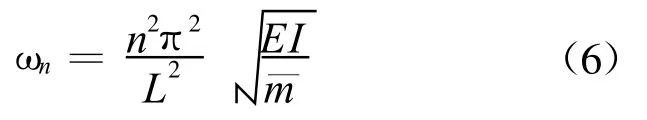
相应的模态函数为

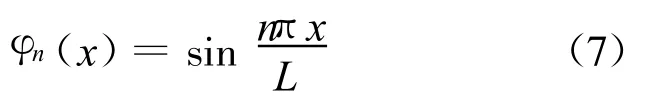
将式(4)～(7)代入式(1),解得结构的动响应表达式为

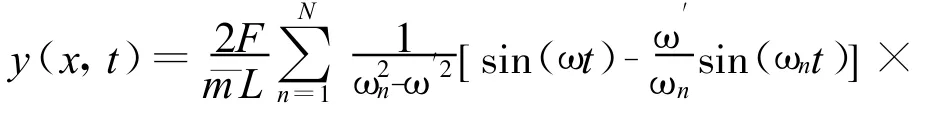
2 有限元模型

由于流体对水中结构的影响较大[8],在动力分析时需要考虑流体与结构的相互作用.因此,本文采用可实现流固耦合分析的三维实体单元和三维声学流体单元进行离散.建模时,实体单元按照结构实际尺寸建立,流体域使用6倍于结构半径的水域代替无限水域.数值实验表明,当流体区域大于固体结构半径的5倍时,其结果与无限流体的计算结果误差小于1%.结构与流体接触面采用FSI(fluid-solid interaction)标记.计算模型如图1所示.计算参数按表1选取.

图1 计算模型及截面图

表1 结构尺寸与材料参数

3 数值计算

分析水中结构在简谐荷载作用下的动力响应,首先进行模态分析,计算结构的固有频率和振型.根据固有频率确定简谐荷载的强制频率范围,进行频域分析得到结构响应频率的曲线.选取响应较大的频率进行时域分析,得到结构响应的时间历程曲线.计算中分析了不同长度、不同介质情况下结构的动力响应.

3.1 模态分析

模态分析中模态的提取方法包括分块兰索斯法、子空间迭代法、缩减法、非对称法、阻尼法等,由于流固耦合问题中系统矩阵为非对称矩阵,所以在此采用非对称法进行水中结构的模态分析,空气中则采用分块兰索斯法.考虑结构在空气和水中的不同情况,对长度为20,25和30 m的模型进行模态分析.频率计算结果如表2所列.

取数值计算结果与式(6)的计算结果比较,最大误差小于1.5%,可见本文计算结果准确.由于本文采用实体单元建模,选取结构两端面最下缘节点进行约束,与公式法中的约束条件略有不同,因此得出的数值解略小于公式解.数据显示,无论是在空气中还是在水中,结构的自振频率均随长度的增加而减小,与实际情况相符.且同一结构的各阶频率在水中的计算结果均小于空气中的频率值,原因是结构在振动过程中,流体对于结构的作用相当于增加了结构自身的质量,使振动频率降低.计算结果显示,水中结构的频率较空气中下降超过5%.因此,为准确进行水下结构的动力分析,应该考虑流固耦合效应.

表2 结构在空气与水中的自振频率

3.2 谐响应分析

谐响应分析是用于确定线性结构在受正弦荷载作用时的稳态响应,目的是计算出结构在几种频率下的响应,并得到响应随频率变化的曲线.谐响应分析能预测结构的持续动力特性,从而验证设计能否成功地克服共振、疲劳,以及其他受迫振动引起的不良影响[9-10].

谐响应分析可采用完全法、缩减方法和模态叠加法等方法进行分析.其中,完全法是采用完整的系统矩阵计算谐响应,并允许系统矩阵为非对称矩阵,基于本文的特殊要求,将采用完全法进行分析.分别计算一定频率范围内简谐激励荷载作用下,三种长度的结构在空气中和水中的位移响应.

输入完整的简谐荷载需要指定荷载的幅值、相位角和强制频率范围.首先结合结构的屈服强度,通过试算确定合适的荷载幅值,取F=500 N.其次,为了解结构对不同频率的响应,根据表2所列频率范围,选择强制频率范围为0～25 Hz.子步数为200,荷载变化方式为阶跃荷载.

根据表1的基本参数计算得到结构跨中节点位移响应的幅值随频率变化的曲线,见图2所示.

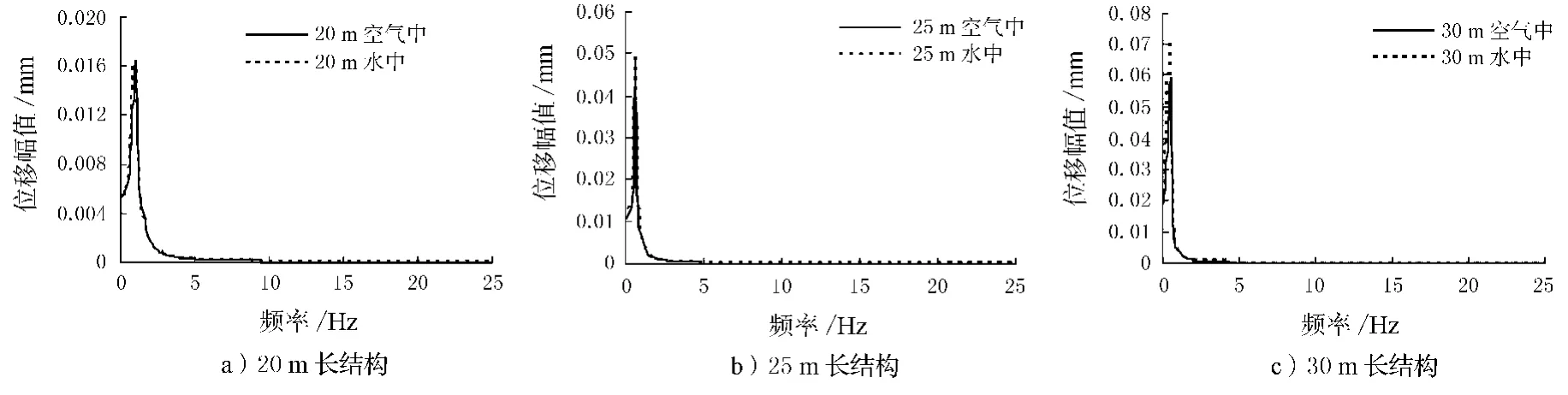
图2 跨中节点位移-频率曲线

由图2中可知,当激振频率接近结构的一阶固有频率时,结构位移响应幅值最大.由于上图计算时受到子步数大小的限制,所求解频率的间隔相对较大,无法准确反应结构在空气中和水中的响应差异.为了进行更准确的分析,需要在更小的频率范围内求解.根据一阶频率的范围,重新选择强制频率范围为0～1.3 Hz,子步数为130,计算后取跨中节点位移-频率关系曲线,见表3和图3.

表3 跨中节点最大位移响应

分析表3和图3可以得出以下结论.

1)由于简谐荷载的频率以很小的幅度从0 Hz增加到1.3 Hz,可以更加接近结构的共振频率,因此图2所示位移响应幅值略大于图1.由于考虑了阻尼,当激振频率接近并略小于结构的自振频率时,位移响应达到最大.

2)图中绘制了三种长度结构的频率响应曲线,随着长度的增加,结构的位移响应增大.

3)简谐荷载作用下,结构在水中的位移响应幅值大于空气中的数值,30 m长的结构在两种介质中的位移响应相差6.8%.

4)同一结构在两种介质中的响应幅值在频率ωs处(空气与水中位移频率曲线的交点)是相同的,当简谐荷载的激振频率小于ωs时,水中结构的响应较大;反之,空气中结构的响应较大.

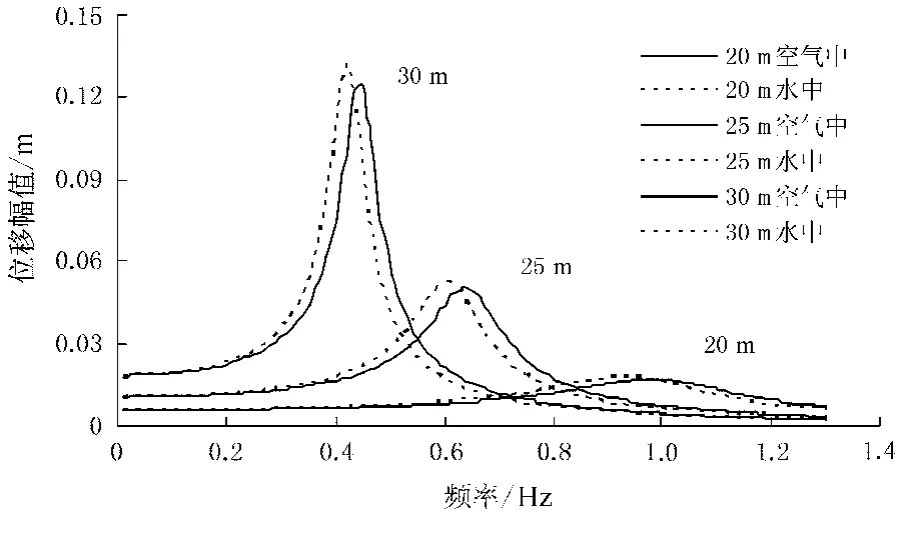
图3 跨中节点位移-频率曲线比较图

3.3 瞬态响应分析

谐响应分析不考虑激励开始时的瞬态振动.瞬态响应分析则可以用于分析结构对任意时变荷载的响应.谐响应分析得出使结构发生共振的频率,再进行瞬态响应分析,可得到结构的位移时程曲线.

瞬态响应分析同样可以使用完全法、缩减法和模态叠加法进行分析.本文选取功能最强的完全法.分别计算频率为ω1,ω2,ω3的简谐荷载作用下,25 m长的结构在空气和水中的位移时程曲线,见图4.

图4 位移时程曲线

由瞬态分析结果可知,简谐荷载作用下,空气与水中结构的响应随时间变化的趋势一致.当以结构的一、二、三阶频率激振时,结构振动的位移幅值依次减小.由于阻尼因素的影响,结构的高阶位移响应迅速衰减.

4 结 论

将海洋悬跨管线、悬浮隧道等两端约束的结构简化为两端简支的Euler-Bernoulli梁,将水流引起的涡激升力简化为作用在结构上简谐荷载,对水下结构在简谐荷载作用下的动力响应进行了频域和时域分析.考虑了水体与结构的相互作用,将不同介质条件、不同长度结构的动响应进行比较分析后得出结论.

1)结构在水中的各阶自振频率小于空气中的自振频率,两者差值大于5%,因此在对水下结构进行模态分析时,有必要考虑流体与结构的耦合作用.

2)结构在水中的位移响应大于空气中的位移响应,当以结构的一阶固有频率激振时,30 m长的结构在两种介质中的位移响应幅值相差6.8%.因此,对于较长的水中结构,在动力分析过程中需要考虑水体的影响.

3)结构在水中与在空气中随时间的振动趋势一致,且位移响应幅值随共振阶数的增大而减小.

[1]秦银刚,曹胜敏.海洋悬空管道非线性振动稳定性分析[J].港工技术,2009,46(3)：27-30.

[2]Gong S W,Lu K Y.Structural analysis of a submarine pipeline subjected to underwater shock[J].International Journal of Pressure Vessels and Piping, 2000,77(7)：417-423.

[3] Patel M H.Three-dimensional behaviour of elastic marine cables in sheared currents[J].Applied Ocean Research,2000,22(1)：45-53.

[4]王变革.水下悬浮隧道锚索的动力响应研究[D].大连：大连理工大学海岸与近海工程国家重点实验室, 2007.

[5]钱 勤,黄玉盈,刘忠族.求附连水质量的一种直接方法[J].力学与实践,1996(5)：19-21.

[6]聂 武,刘玉秋.海洋工程结构动力分析[M].哈尔滨：哈尔滨工程大学出版社,2002.

[7]邹经湘.结构动力学[M].哈尔滨：哈尔滨工业大学出版社,1996.

[8] Lei Fan,Yang Jixing,Xie Xizhen.The numerical calculation research on dynamic characteristics of pipe conveying fluid[C]//Recent Advances in NonlinearMechanics 2009,Kuala Lumpur：Springer, 2009：72-73.

[9]王广地.波流作用下悬浮隧道结构响应的权值分析及试验研究[D].成都：西南交通大学桥梁与隧道工程学院,2008.

[10]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社,2007.