潜水器水动力系数计算方法研究＊

张 赫 庞永杰 李 晔

(哈尔滨工程大学智能水下机器人技术国防科技重点实验室 哈尔滨 150001)

0 引 言

操纵性是潜水器综合性能的组成部分之一,是潜水器总体性能设计的重点,良好的操纵性能是潜水器安全航行和充分发挥其战技术水平的重要保证[1].水动力系数是潜水器操纵运动方程的系数,基于潜水器操纵运动方程模拟潜水器操纵运动并预报操纵性能,必须先确定水动力系数.目前求取水动力系数的方法主要有4种：半理论半经验的估算方法、计算流体力学(compute fluid dynamic,CFD)仿真计算、拘束或自由自航模型试验和实航数据的系统辨识.由于系统辨识的方法一般用于实航数据的分析和水动力系数的修正,不便于指导潜水器的操纵性设计.本文的研究工作着重于前3种求取方法,以某长航程潜水器作为研究对象.在“迭加原理”和所谓“相当值”的基础上,根据等值椭球和等值平板理论,应用近似公式的估算方法求取潜水器的水动力系数;接着基于势流理论面元法编制程序计算潜水器水动力系数.随后应用近年来发展迅速的CFD技术,对某长航程潜水器的周围流场进行模拟构建,给出潜水器受力情况的数值模拟,完成了计算机上的拘束船模试验,得到了相应的水动力系数.同时通过与循环水槽实验数据的对比,验证了该模拟工作的可行性与准确性.最后,通过对上述几种常用计算方法的比较分析,总结了不同计算方法的适用条件和计算精度.

1 潜水器水动力系数的计算原理及结果

1.1 计算模型

某长航程潜水器主体为椭球体,其中首部为标准半椭球体,中部为椭圆柱,尾部为不规则椭圆锥形状,同时配有4个水平翼和一个垂直舵.如图1所示.

图1 计算模型(CAD视图)

1.2 基于近似公式估算水动力系数

依据经验公式和查询图谱,在“叠加原理”和所谓“相当值”的基础上,假定潜水器的水动力系数(如速度系数、速度系数、角速度系数)等于艇体和各附体(舵、翼等)的水动力系数之和,同时计及艇体与各附体的相互影响;并认为艇体和各附体分别可用等值椭球体及等值平板的理论计算结果来确定[2].计算得到的线性水动力系数如表1所列.

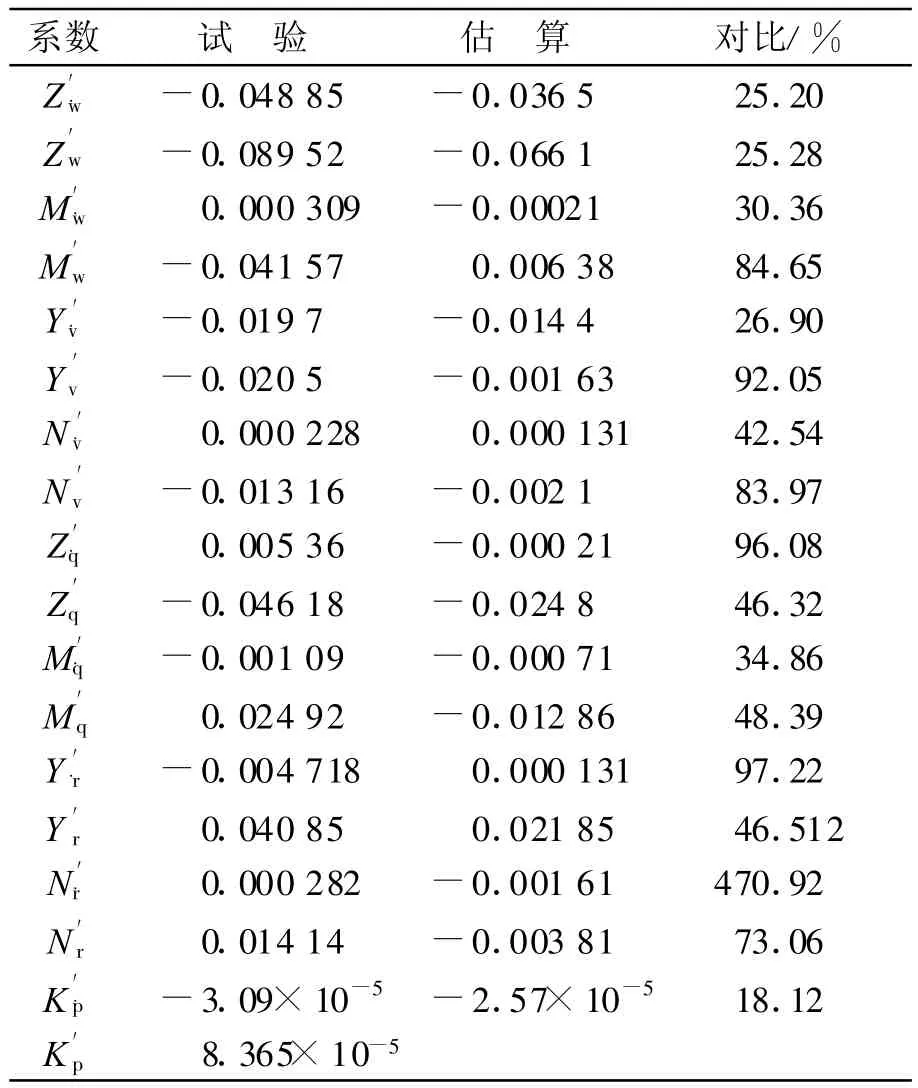
表1 近似公式估算结果并试验结果对比

1.3 基于面元法计算惯性类水动力系数

根据理想流体力学相关理论[3](无界流中运动物体的受力、附加质量概念、Hess-Smith方法、四边形单元的诱导速度公式、积分方程的数值解法),在无界流场中,在物体表面上分布源汇,然后利用Hess-Smith方法求解关于源汇强度的积分方程,确定流场在整个空间的状态(空间各点的诱导速度势).根据诱导速度势附加质量,计算得出作用于物体上的惯性类水动力[4].在上述理论的基础上,本文所用面元法计算惯性类水动力系数的流程如图2所示.

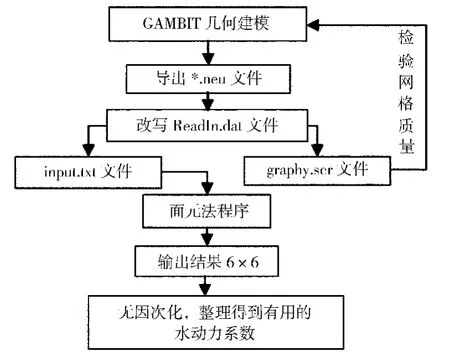
图2 面元法计算水动力系数的流程

1.4 应用CFD软件数值求解水动力系数

本文提出的是一种基于计算流体动力学CFD软件FLUENT的模拟循环水槽试验方法.首先应用FLUENT前处理软件GAMBIT建立研究对象模型及控制域;在模型表面布置三角形网格,进而在控制域内布置非结构化网格;设定边界条件,加入用户自定义函数(user define function,UDF)文件,引入动网格技术[5-8],采用基于完全非结构化网格的有限体积法,实现平面运动机构实验进行的纯横荡运动、纯升沉运动、纯摇艏运动、纯俯仰运动和纯横滚运动;对FLUENT得到的力与力矩系数应用MATLAB傅里叶展开, EXCEL最小二乘法拟合,无因次化得到垂直面和水平面的水动力系数以及相关的流体动力分析.

用于数值求解的实体模型如图3所示,建好实体模型后,要根据其尺度选择合适的控制域.根据无界流场的概念和计算模拟工作的需要,控制域与模型长宽高比大约7∶1,此时水动力系数受潜深变化的影响最小.采用的控制域为一长方体以利于设定边界条件,潜水器坐标原点建立在模型长度的中点处,在设计的初期假定重心点位于此处.数值求解坐标系取潜水器操纵性中常用的坐标系,即：x轴取指向船艏为正,y轴取指向右舷为正,z轴取向下为正.将整个控制域分成3块,使得保证划分的网格质量和体积能连续变化的基础上,同时反映出流场的基本和关键信息.综上,控制体与潜水器相对位置及控制体分块情况如图4所示,计算结果、与面元法和水槽试验的对比结果见表2.

图3 计算实体模型(1∶1)

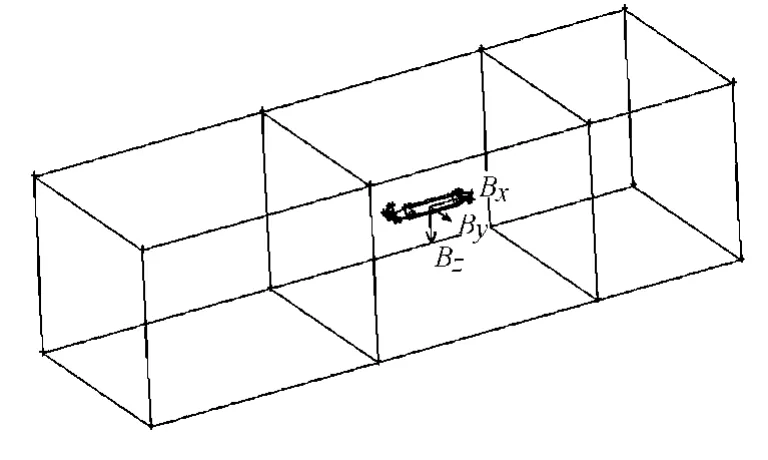
图4 控制体与潜水器相对位置

表2 FLUENT计算结果与试验值、面元法结果对比

2 三种计算方法的结果对比分析

在上节不同方法的计算数据及对比百分比的基础上,综合评价、总结不同计算方法的特点、适用性.

利用近似公式估算方法能够得到23个水动力系数,其中惯性类系数9个、速度类系数4个、角速度系数4个、舵角系数6个(由于本文的研究重点不包括舵翼,所以此6个系数没有给出).根据获得的结果还能推算出耦合类水动力系数13个.这种估算方法在模型的尺度和舵翼位置量等基本信息已知的情况下即可完成,所需的计算时间少,得到的系数较多.通过对其中惯性类和速度类的16个系数与试验值对比得知,和试验值符号相同,且大小均在同一个数量级上,最大的百分比误差为48.4%;而虽和试验值相同符号,数值却差一个数量级同试验值相比符号相反,其中同比误差30.4%,比试验值小一个数量级.通过符号与大小的比较,其中10/16个系数估算效果较好.分析造成计算差异的原因：近似公式估算中大部分系数的获取是通过对椭球体附加质量与冲角导数、角加速度等曲线的插值得到的,由于本模型是个不规则的扁平体,使得许多值是由外插才能得到,在一定程度上降低了数值的准确性.综上,应用近似公式估算潜水器各水动力系数适用于设计的最初期,特别适用于主体为较规则的椭球体潜水器,能够得到该设计模型水动力性能优略的基本评价,同时也能为后续水动力试验结果的评价提供依据.

根据计算流体力学的势流理论,面元法能够得到潜水器的36个附加质量,再根据附加质量与惯性类水动力系数的对应关系,可以得到相应的系数.这36个系数的数值大小与分布规律验证了模型的对称特性.通过对该潜水器不同模型、不同网格划分时结果的比较分析,在保证网格近似正方形特点并在附体处做加密处理的基础上,网格数目的多少对于结果影响不太大,所以计算的时候采用较少的网格就能在较短的时间能得到较为准确的潜水器附加质量.同时,本文通过面元法计算结果和FLUENT模拟平面运动机构试验得到的9个惯性类水动力系数进行比较,得到FLUENT计算的结果和面元法结果有很好的拟合度,前者一般比后者大10%以内,只有一个结果相差24%,但数量级在10-4,两者绝对值相差也很小.综上,应用面元法进行水动力系数的求解,在较好的完成模型网格划分的基础上,能够在较短的时间内得到所有惯性类水动力系数,结果比较准确.不足的地方在于,由于该计算方法基于势流理论,没有考虑到流体粘性作用,所以得到的值有一点偏小,另外该方法的计算不能得到对于潜水器运动作用同样重要的速度、角加速度系数,所以建议和其他方法一起使用,获取全面的水动力系数.

借助于流行的商用计算流体力学软件FLUENT模拟潜水器循环水槽试验,能够解算得到真实水槽试验能够得到的全部水动力系数.通过模拟平面运动机构试验能够得到惯性类水动力系数9个,速度类系数8个,与面元法比较,两者符号均相同,数值也很接近.通过和试验值的比较,纯平动(包括升沉运动和横荡运动)计算值(除Z′w和)外误差较小,通过改变网格数目与网格分布,和改变效果不明显,仍旧偏大,所以在实际预报时建议采用相对误差较小的模拟斜航试验结果;纯转动(包括俯仰运动和摇艏运动)计算值误差相对偏大,造成这种结果的原因是两个模型的转动中心点之间略有距离(在设计的初期很难得到准确的转动中心,所以计算中心取在长度中心点.笔者以为在保证相同中心点的情况下计算精度应该有所提高,具体体现于面元法与模拟试验结果良好的拟合性).此外,根据潜水器模型的对称特性,附加质量系数应近似满足即.考察可知可以认为和和基本相等,即满足附加质量相互关系.综上,应用商用软件FLUENT进行水动力计算是可行的,尤其是在模型纯平动运动时;若能保证转动中心位置重合,纯转动运动的精度也会有所提高;同时计算结果对模型形状对称性的验证,也在一定程度上证明了结果的准确性.该方法的提出相比传统水动力水槽实验,能够节省相当的人力、物力和财力,是一种比较经济节能的方法.

3 结束语

本文以某长航程潜水器为研究对象,分别采用了3种不同计算方法得到了潜水器的水动力系数,从而满足了在设计初期对操纵性能进行研究评价的需求.通过近似公式估算的方法实用于设计的最初期,特别适用于主体为较规则的椭球体潜水器,能够得到该设计模型水动力性能优略的基本评价;基于势流理论的面元法计算适用于模型设计完成之后,能够得到对于操纵性影响较大的惯性类水动力系数,配合其他方法才能完成全部的性能预报工作;最后提出的基于计算流体力学软件的模拟试验方法,能够预报潜水器模型试验全部水动力系数对比真实试验结果具有相当的精度,为水动力系数的计算工作提供了一种有效的求解新途径.

[1]徐玉如,苏玉民,庞永杰.海洋空间智能无人运载器技术发展展望[J].中国舰船研究,2006(3)：1-4.

[2]孙元泉,马运义,邓志纯.潜器和深潜器的现代操纵理论与应用[M].北京：国防工业出版社,2001.

[3]施生达.潜艇操纵性[M].北京：国防工业出版社, 1995.

[4]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京：国防工业出版社,1998.

[5]张 玲,谢殿伟.水下机器人惯性类水动力计算研究[J].船舶,2004(3)：8-10.

[6] Fluent Inc.,Gambit modeling guide[M].Fluent Inc.,2003.

[7]Fluent Inc.,Fluent user＇s guide[M].Fluent Inc., 2003.

[8] Fluent Inc.,Fluent user defined function manual [M].Fluent Inc.,2003.