干燥路面上轮胎制动距离的FEM仿真
2011-02-27臧孟炎陈玉祥
臧孟炎,陆 波,陈玉祥
(华南理工大学机械与汽车工程学院,广州 510640)
前言
汽车的制动性能是有效减轻或避免交通事故的一个重要因素。随着交通法规越来越严格,要求各个汽车生产厂家必须公布每款产品从 100km/h开始制动到完全静止时所行驶的距离,但到目前为止,汽车的制动距离通常只能通过试验得到。为了既满足交通法规要求又缩短产品开发周期,在产品设计阶段,通过数值仿真方法对汽车的制动距离进行有效预测非常重要。
众所周知,轮胎是汽车与路面的唯一接触部位,汽车制动基本上依靠轮胎实现(风阻有一定贡献)。所以,在某种意义上,可以认为轮胎的制动性能决定汽车的制动性能,特别是主机厂选配轮胎进行制动性能评价时尤为如此,因为此时除轮胎不同外,其他部分完全一样,汽车制动性能的优劣取决于轮胎的制动性能。
然而,在有限元仿真分析方法广泛应用于汽车及主要零部件各种性能评价的今天,对轮胎制动性能的分析和评价,目前仍然主要依赖试验。究其原因,主要是轮胎制动过程伴随着大变形和冲击,隐式有限元方法难以应对而只能寄希望于显式有限元方法。但是,汽车的制动过程特别是湿滑路面的制动时间长达数秒,冗长计算时间和数据累计误差使显式有限元方法难以实现完全模拟,而且没有实际工程意义。为此,文献[1]和文献[2]中提出了根本解决上述问题的离散化方法:将制动过程按速度离散化,通过显式有限元分析各离散速度下的制动器摩擦热损失率和轮胎与路面的摩擦能量损失率,再近似求得制动时间和制动距离。
本文中在介绍制动过程离散化仿真分析方法的基础上,具体分析光面轮胎在干燥路面的制动时间和制动距离,以确认其计算效率和精度,作为花纹轮胎干湿路面制动性能仿真分析的基础。
1 制动过程分析
图1为常用汽车制动系统。汽车制动时,驾驶员通过制动踏板压缩连接于制动主缸和制动轮缸软管中的制动液,使制动器工作。可以近似认为,汽车的动能通过制动器的摩擦热损失和轮胎与路面间摩擦能量损失而消耗,直到汽车静止。
尽管空气阻力和轮胎的黏弹性变形等因素也消耗汽车动能,但与上面两个因素相比,可忽略不计。
制动时轮胎的动力学模型如图 2所示,其中 G为1/4车质量;Fz为轮胎受到的地面反力;rs为轮胎滚动半径;Fxb为轮胎受到的地面摩擦力,以速度v行驶的汽车制动时,制动器通过对轮毂施加制动力矩Tμ,轮毂转动角速度 ωw下降,导致轮胎接地部分与地面产生相对滑移速度vs。轮胎滑移率为
轮胎滑移率是影响制动效果的重要因素。当车轮抱死,轮胎与地面间处于完全滑移状态时,制动力系数明显下降,远远低于滑移率为 15%时的数值,汽车容易出现跑偏或失去转向能力。为此,目前已作为乘用车基本配置的 ABS系统根据轮胎滑移率的大小,通过控制制动轮缸压力以调节制动摩擦面之间的结合强度,保证制动力系数在较高的水平。
2 轮胎制动过程离散化仿真
2.1 制动过程离散化
将整个制动过程按制动速度离散成多个区间,假设汽车初始制动速度为 100km/h,可将整个制动过程以速度划分为 10个区间,区间端点速度分别为100,90,…,0km/h,参见图 3。在每个离散速度下,建立该速度下的轮胎制动分析有限元模型,考虑ABS的作用使轮胎与路面间保持最佳滑移率(15%)来模拟制动过程,通过仿真结果求得该速度下的制动器摩擦热损失率和轮胎与路面间摩擦能量损失率,然后使用分析方法近似求得制动时间和制动距离。这样,“漫长”的制动过程有限元仿真分析转化为 10个速度下简单的制动仿真计算。
2.2 制动分析有限元模型
如图2所示,轮胎制动时汽车前进速度为v,而车轮绕轮轴转动的角速度为 ωw。为分析各制动速度(如50km/h)下的轮胎变形和应力状态,须要按图 4所示的线性加载方式给车轮转动中心施加一个强制平移速度,同时为刚性车轮定义一个适当的、也是线性增加的转动角速度以确保开始制动计算时轮胎滑移率为 15%。10个离散速度均采用图4的加载方式,在 60ms内加载,20ms用于制动分析。只是在20和10km/h时,ABS失效,车轮抱死,转动角速度为零。轮胎的充气和汽车整质量加载过程只需进行一次有限元分析,然后将轮胎应力和位移信息作为各个加速制动过程的初始状态即可。
2.3 制动轮缸压力计算
用有限元法对制动距离的仿真评价很大程度上取决于所采用的制动轮缸压力曲线pc(v)的可靠性。紧急制动时滚动阻力一般只有制动力的几十分之一,空气阻力也可以忽略不计,因此一般只考虑轮缸压力、制动力矩以及地面制动力对车轮系统的作用。在 0~100km/h的速度区间内,轮胎的振动频率远小于滚动轮胎 1阶固有频率,所以文中不考虑轮胎的周向扭转振动传递效应[3-5]。根据汽车ABS系统的控制与作用机理[6],轮胎的动态平衡关系为
式中:m为整车质量;It为单个轮胎的转动惯量;n为轮胎个数;μs为路面与轮胎间的摩擦因数;FI为某个离散速度下轮胎接地区域节点所受地面垂直反力;N为轮胎与地面接触区域节点个数。
联立式(1)~式(4)方程可以得到单个轮胎制动力矩为
采用盘式制动器时制动轮缸压力为
式中:pc为某个离散速度下制动轮缸的输出压力;Ac为制动软管横截面积;rc为制动钳有效作用半径;μc为制动盘上的摩擦因数。
图5为ABS作用下制动轮缸压力输出曲线,通常可以把轮缸压力大体分为A、B、C 3个区域:制动轮缸压力经tA=0.25s的上升阶段到达区域B;当汽车速度≤20km/h时,车轮被完全锁止到达区域C。在制动过程的仿真计算时,假设汽车前后轮制动轮缸的压力按照相同的规律变化,区域 A轮缸压力线性上升。
利用有限元仿真软件求得每个离散制动速度下的Fxb,多项式插值求得Fxb(v),通过式(5)~式(6)获得pc(v)。
2.4 制动距离求解
根据能量守恒定律可得
在制动过程中轮缸压力输出与制动速度间存在明显的非线性关系,把前面所分 10个速度区间 Δvi(i=1,2,…,10)再次细分成以提高仿真估计精度。在每个小区间内,减少的汽车动能等于制动器摩擦热损失和轮胎摩擦能量损失之和(参照图3),汽车速度从下降到的时间可以由下式得
假设A区域的滑移率为15%时,制动时间T与制动距离S分别为
式中v(t)为未修正的速度曲线。
由于区域A是制动液压力的上升阶段,而上面求得的制动时间与制动距离是假设轮胎在区域A的滑移率为 15%的条件下得到的,为了修正这两个值,假设在这个区域路面对轮胎的摩擦力是线性增加的。由汽车动态平衡可得
因此,tA时刻的汽车速度和在区域 A的制动距离分别为
总的制动时间与制动距离可以通过下式修正:
式中:T|v=vA、S|v=vA分 别为汽车从减速到所经历的时间与距离。
以上就是轮胎制动过程离散仿真分析的基本方法。由图 4可知,每个离散速度下轮胎有限元制动仿真的时间只需要80ms,对于制动时间长达5s的制动问题,该方法是完整计算所需CPU时间的1/60以下。这样,一方面可以大大减少数据累计误差,以保证计算结果的可靠性;另一方面,使用多CPU计算机对 10个制动速度同时进行计算,保证了该仿真方法的工程应用价值,使轮胎干湿路面制动性能的仿真分析成为可能。
3 轮胎制动性能仿真分析实例
本文中使用 175/65/R14型号轮胎,为简便起见,以不考虑花纹的光面轮胎在干燥路面的制动过程为研究对象,使用软件Abaqus,以确认100km/h速度下制动过程离散仿真方法的有效性。
3.1 轮胎有限单元和材料模型
图6为轮胎有限元模型截面图。子午线轮胎中的帘布、胎冠、胎体与胎圈内嵌钢丝帘线,使用rebar加强型单元嵌入橡胶基体单元的方法来模拟骨架材料对轮胎橡胶的增强作用。为了节约仿真计算时间,使用与胎圈外围共节点的离散刚体单元模拟轮辋,路面使用解析刚体。
使用yeoh本构关系模型[7],以及泊松比0.495模拟橡胶材料特性,钢丝帘线使用线弹性材料[8]。
3.2 制动模型和边界条件
轮胎制动工况有限元模型施加边界条件包括充气、加载、加速和制动 4个步骤。充气工况在2D模型中完成,然后利用Abaqus软件中*Symmetric Model Generation与*Symmetric Results Transfer两个关键字,将其转换为 3D模型,并完成汽车整车质量的加载。这两个工况使用隐式计算方法完成。利用*Import关键字将前两个工况隐式计算结果导入,在动态显式计算步中完成轮胎的加速与制动工况。表 1为本实例的相关参数。按图 4所示的加载方式分别建立 10个离散速度下的轮胎制动分析模型进行制动仿真计算。
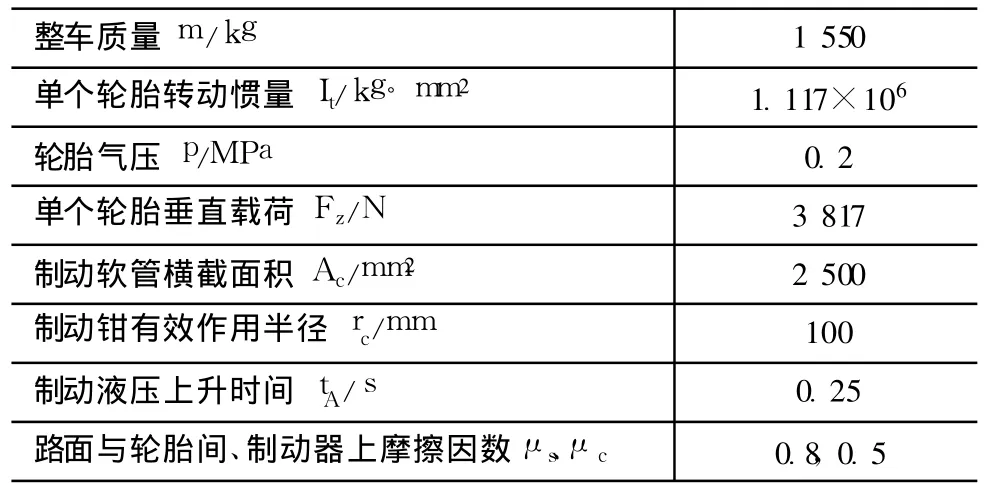
表1 制动仿真参数
4 结果分析
由于制动分析采用显式有限元法,在每个离散速度的制动平衡阶段存在如图 7所示的振动现象,通过获得明显的振动周期来确定制动平衡仿真计算时间,由Abaqus软件获得某一离散速度下均匀分布的 20个时刻点上的轮胎接地区域节点滑移率与受到的垂直反力,利用式(2)和式(9)并取其均值,得到该离散速度制动工况下的与,同理得到其它9个离散速度下的(图8)。在30~20km/h这个速度区间上,轮胎滑移率从 15%很快提高到100%,所以轮胎摩擦能量损失率有一个上升过程,在其他区间轮胎摩擦能量损失率均随制动速度的降低而下降。
根据 10个离散速度下轮胎所受地面摩擦力的分布特点,对其进行3次多项式插值得到Fxb(v),如图9所示。通过式(5)~式(6)就可得到制动力矩Tμ(v)与轮缸压力pc(v)。
根据pc(v)与表1的相关参数,并利用式(8)就可求得(图10),当汽车速度≤20km/h时车轮完全抱死,制动器上的摩擦热损失为零。曲线在30km/h处有拐点,这是由于轮胎滑移率变化所致(从15%变化到100%)。
轮缸压力上升阶段tA=0.25s时,对应的制动速度为94.52km/h,由式(17)和式(18)修正后的制动时间为4.7s,制动距离为48.11m。
根据汽车制动距离计算公式[9]:
式中:τ′2为制动器间隙时间;τ″2为制动轮缸压力上升时间;ua0为制动初速度;abmax为最大制动减速度。对应于文中所假设的仿真制动参数,τ′2=0, τ″=0.25s,ua0=100km/h,abmax=μsg=7.856m/s2,最后得到S=51.7m。式(18)与式(19)得到的计算结果接近,说明文中仿真方法可行、有效。
5 结论
建立了 175/65/R14光面轮胎制动工况有限元模型,对求解配备 ABS制动系统汽车的制动时间与距离的仿真方法做了详细介绍。此方法能反映制动系统相关参数、轮胎的结构与材料对制动距离的影响。通过仿真实例验证了该方法的可行性与有效性,为复杂花纹轮胎干湿路面上的制动距离仿真预测奠定基础。
[1] Cho JR,Kim KW,YooW S.Mesh Generation Considering Detailed Tread Blocks for Reliable 3D Tire Analysis[J].Advances in Engineering Software,2004,35:105-133.
[2] Cho JR,Lee HW,YooW S.A Wet-road Braking Distance Estimate Utilizing the Hydroplaning Analysis of Patterned Tire[J]. Int.J.Numer Meth.Eng.,2007,69:1423-1445.
[3] 庄继德.汽车轮胎学[M].北京:北京理工大学出版社,1997: 285-320.
[4] 程刚,袁文生.子午线轮胎振动特性试验研究[J].弹性体, 2006,16(4):7-10.
[5] 乔维高,何耀华.车辆运行时轮胎的振动特性[J].农业机械学报,1999,30(2):22-26.
[6] 吴诰珪,叶峰磊.基于制动轮缸压力的汽车ABS滑移率的计算[J].公路交通科技,2002,19(3):134-136.
[7] Yeoh O H.Characterization of Elastic Properties of Carbon Black Filled Rubber Vulcanizates[J].Rubber Chemistry and Technology,1990,63(5):792-795.
[8] Simulia.Software Corporation,ABAQUS6.8-1(Dcumentation) [G].Abaqus Analysis User's Manual,2008.
[9] 余志生.汽车理论[M].北京:机械工业出版社,2007:96-100.
