传送带输送流体流量计算方法研究

郭仁东，胡记磊，王春霞

（1.沈阳大学 建筑工程学院，辽宁 沈阳 110044;2.沈阳机电研究设计院，辽宁 沈阳 110006）

传送带输送流体流量计算方法研究

郭仁东1，胡记磊1，王春霞2

（1.沈阳大学 建筑工程学院，辽宁 沈阳 110044;2.沈阳机电研究设计院，辽宁 沈阳 110006）

根据流体薄层运动理论，给出了在水环境漂浮物处理去除工作中，采用输送带输送流体漂浮物的方法，将水中漂浮的油污物质或浮萍等类流体物质，从水中分离并输送到采污船或岸上，给出了其输送量的两种计算方法。第一种方法是经典的纳维埃-斯托克斯方法，第二种方法是流速直线分布法，文中并对两种方法的计算结果加以比较并给出结论。

流体薄层运动理论；输送带；漂浮物；纳维埃-斯托克斯方法；流速直线分布法

1 绪论

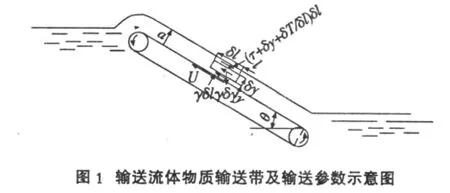
在水环境保护中常要将海水表面的油污进行收集分离并输送到船上或岸边，然后在进行处理，对内陆的淡水湖也有被油污或浮萍等漂浮物污染的现象，也可以采用同样的方法进行分离、输送。现阶段经常采用的输送方法是利用平面输送带，将输送带安装成与水平面成某一个合适的角度，一般为15°～25°，一个传输装置安装在一只船上用来收集海水边的或湖水里的污染物，如油、藻类等漂浮物。该漂浮物厚度足够厚使被带走的物质不受到装置功能的限制。传输带以恒定的速度U运动，如图1所示，带的长度能够深入水中使要被传送的流体均匀地卷到输送带上。通常的做法是，第一步根据流体力学纳维埃-斯托克斯公式导出输送流体，自由表面为大气压（相对压力为零）时的力的平衡方程式，再进行不定积分代入边界条件；第二步得出流体被输送物厚度内的点流速分布；第三步运用流量计算公式对点流速分布公式进行定积分，积分计算单位宽度传输带带走的油量；第四步，根据输送带倾斜角θ，输送带转动线速度U和漂浮物的黏性特性μ,重度γ的关系计算实际漂浮物的输送量[1，2]。由于输送带上的流体物质厚度很薄，沿厚度方向的点流速分布可近似看作线性分布，所以同时采用流速线性分布法对某一特殊的工程实例进行流量计算，并与经典的纳维埃-斯托克斯方法进行比较。

2 纳维埃-斯托克斯方法应用与计算

2.1 被输送流体物质单位皮带宽度内流速分布及流量计算

现设某一单位宽度薄层的运动点速度为u，由于传输带上所携带的流体物质表面是与大气接触的自由表面，因此纳维埃-斯托克斯方程中的压强变化忽略不计，而且流速为稳定流，则可得到下式。

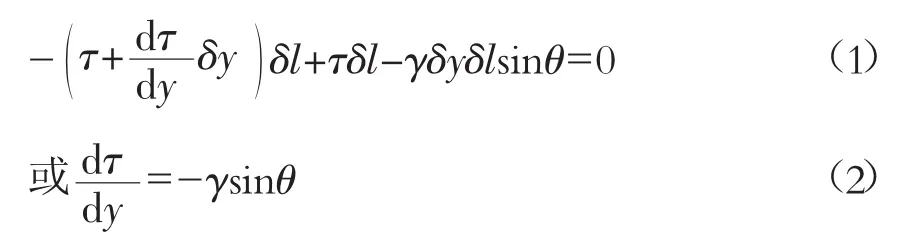
式中：τ——沿斜面微小流层单位面积摩擦应力（剪切应力）；y——垂直斜面的坐标值；l——从下向上沿斜面方向的坐标值；γ——流体物质的容重；θ——斜面与水平面的夹角。

当表面剪切应力作用认为是0时，积分结果为：

这个方程式代入牛顿黏性定理，τ=μdu/dy，得出

上式积分得点速度分布为

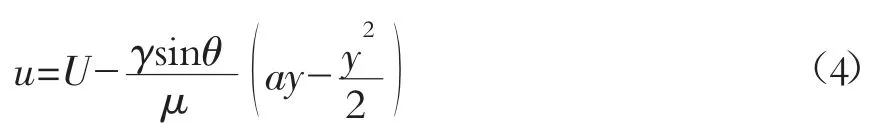
从（4）式中可以看出点流速u的分布是垂直坐标y的函数，根据流体力学中流量计算的定义，通过积分计算给出单位宽度传输带所输送的流体物质的单宽流量为：

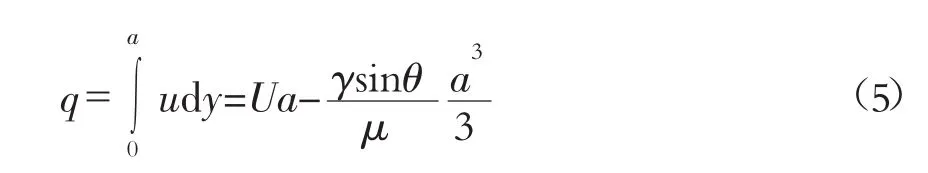
这个表达式说明流量与传送带的速度U，流体物质层厚度a，传送带倾斜角度θ，流体物质的容重γ，及流体物质的动力黏度μ有关。

2.2 单位输送带宽度内的最大单宽流量计算

当其他输送条件确定后，即在流体容重γ，流体动力黏度μ，输送带线速度U，以及输送带倾斜角度θ都确定的前提下，根据函数存在最大值理论，可以通过令偏导数dq/da等于0，得出特殊的a值，来获得单位宽度输送带的最大流量qmax。

在某些特定的场合或在输送带顶部对被输送流体物质的层厚加以限制则，将上式（6）中的最佳流体物质厚度a代入式（5），得单位宽度输送带最大流量为：

3 点流速近似线性分布法应用及计算

3.1 缝隙流动点流速线性分布的应用现状

点流速线性分布公式的经典流体力学理论中，对于两固体间小空间内流体的流动，又称缝隙流动或薄层流动。这种流动所用的理论根据是牛顿内摩擦定律，又由于垂直运动方向的流体物质厚度很小，人们常常把垂直流动方向的点流速分布假设为线性分布。比如在汽缸与活塞之间缝隙中的润滑油，由于活塞运动带动紧靠活塞表面油层以同样速度流动。又如测量某种流体物质动力黏度的装置，也是假设转动圆筒的转动部分与固定不动部分之间空隙内流动物质点速度分布为直线分布[3，4]。可见，这种假设经过人们长时间生产实践得出的可靠结论。输送带输送流体物质的工作状态就是属于空隙流动或薄层流动理论。因此，我们可以采用线性流速分布来求出单宽输送带流量[5]。

3.2 点流速线性分布计算公式推导

假设输送带垂直流体物质方向流速分布的表达式如下

3.3 点流速线性分布情况下流量计算

在上一节中，求出了点流速线性分布表达式（10），根据公式（10）进而求出输送带输送流体物质的单宽流量q，根据流体力学用点流速求流量的定义，计算公式如下：

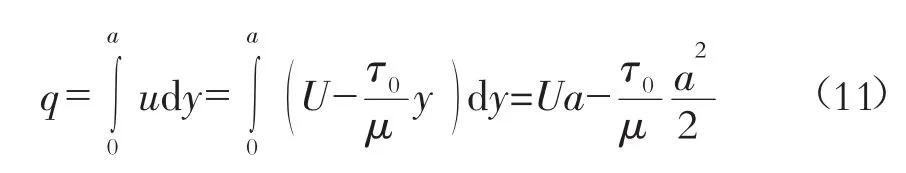
4 纳维埃-斯托克斯方法与直线分布法流量计算结果的比较

在文中讨论了纳维埃-斯托克斯公式所导出的输送带输送流体物质单宽流量的计算公式，又给出了同样工作条件下点流速线性分布的单宽流量计算公式。下面将根据一个具体的工程实例，所抽象给出的皮带输送流体物质计算参数，采用两种方法得出流量，并进行比较讨论其计算结果。

例：如上图所示，皮带运动速度为U=5 m/s，由摩擦力而输运的油层厚度为a=2 mm，皮带倾角θ=20°油的黏度 μ=0.02 Pa·s,比重为 0.8，油层压强均为大气压，试求皮带宽度b=0.7 m所输送的流量及油层的平均速度。

4.1 纳维埃-斯托克斯方法计算流量

根据公式（5）代入例题所给出的参数并计算出实际宽度输送带流体物质流量如下

单宽流量为

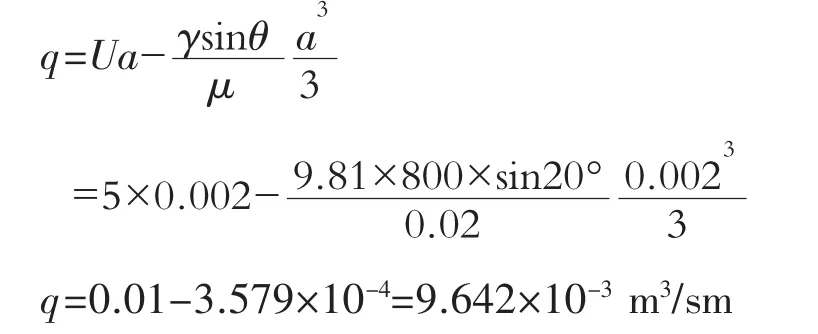
通过输送带宽度b的流量为

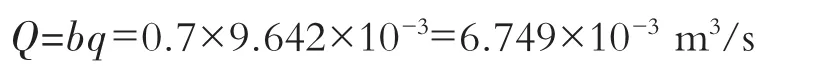
4.2 点流速直线分布法计算流量

根据公式（11），代入例题所给出的参数并计算出实际输送带流体物质流量如下。单宽流量为：

τ0×1×1=γ·sinθ·a×1×1 即 τ0=γsinθ·a 代入上式，有

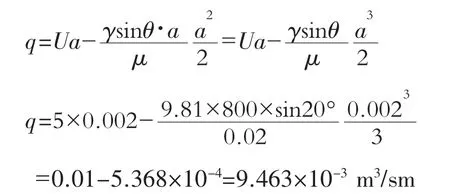
通过输送带宽度b的流量为：

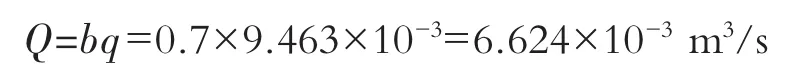
4.3 比较两种方法所得流量及其误差

将上两节所得流量加以脚标，纳维埃-斯托克斯方法所得流量为Qn，而直线法所得流量为Qz，则有其绝对误差为d及相对误差d%如下：

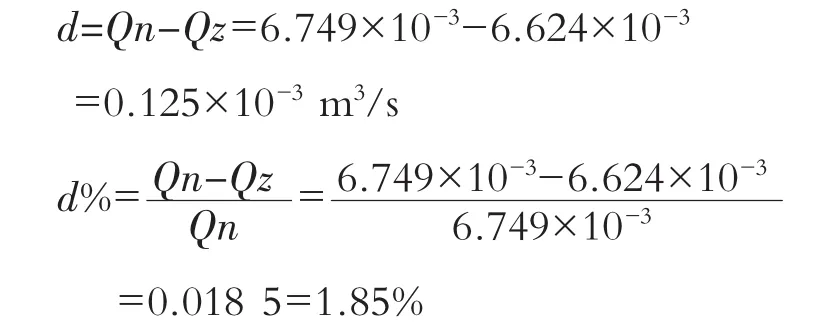
通过两种方法可知：其相对误差为1.85%，采用点流速方法求流量，其计算精度可以满足工程要求。采用点流速法可将公式变形为求出薄层自由表面流速u0，再取u0与带表面线速度U的算术平均流速，利用连续方程求流量则更为方便，计算简单，利于工程技术人员掌握。

［1］段文义，郭仁东，李亚峰.水力学［M］.沈阳：东北大学出版社，2001：10-15.

［2］段文义，郭仁东，李亚峰.流体力学［M］.沈阳：东北大学出版社，2001：12-23.

［3］郭仁东，冯劲梅，吴慧芳.水力学［M］.北京：人民交通出版社，2006:5-19.

［4］Victor L.Streeter,E.Benjamin Wylie,Fluid Mechanics(Seventh Edition)［M］，New York：McGraw-Hill Book Company,1979:182-189.

［5］郭仁东，等.圆管流体平均流速与管道半径的关系［J］.沈阳大学学报，2008,20（1）：1-3.

Study on flow calculation method of fluid transported with conveyer belt

GUO Ren-dong,HU Ji-lei,WANG Chun-xia

Based on the thin fluid layer motion theory,the paper describes the method,transporting fluid floater with conveyer belt,to remove floater in water.The floating oil pollutant or duckweed is separated from the water and sent to the mining sewage ship or bank.The paper puts forward two methods to calculate the transportation quantity.One method is classic Navier-Stokes,another is linear flow velocity distribution.The paper compares the calculation results of the two methods and gets some conclusion.

fluid thin layer movement theory;conveyer belt;floater;Navier-Stokes;linear flow velocity distribution

X52

B

1002－0624（2011）06－0060－01

2011-03-04