基于DEM的小流域坡长计算方法研究
2011-02-23胡洁,王程
胡 洁,王 程
(1.西北农林科技大学 资源环境学院,陕西,杨凌,712100;2.西北大学 城市与环境学院,陕西西安710127)
目前,坡长的定义比较混乱,没有形成完整统一的框架。在流域地貌学中,坡长定义为斜坡在一定的角度上最短的长度,也叫地表线径流的长度。R.E.Horton[1]认为,地表径流线长度是指从径流出现的那一点到集中于一定槽床以前沿地表流动的距离,该距离等于两水道间的平均距离的一半。然而在实际研究中,坡面形态往往是不规则的,非常复杂且不易考察完整坡面,Foster和 Wischmeier[2]提出了对不规则坡面做分段分析处理的方法,每一分段的坡长可以看作是上游各分段坡长值的累加。周启明、刘学军等[3]认为坡长是由给定点逆流而上到水流起点(又称源点)之间的轨迹(也称水流路径或流线)的最大水平投影长度。然而该定义并没有考虑到径流在坡面的沉积即截断因子的概念。这种概念其实就是将坡长等同与经流线长度。但事实上坡长与径流线长度不是一个概念;坡长应该有一个起点和终点,当坡面上发生沉积时,坡长重新开始计算,但是径流线长度则可能连续计算;坡长是有限度的,径流长度值会很大。本文选择在土壤侵蚀中坡长概念,分析不同坡长提取方法的优缺点
1 基于DEM的小流域坡长提取
国内外对DEM的小流域坡长计算进行了很多的研究,Hickey等[4,5]计算每个格网单元到起点的最大累计水流长度作为该格网到坡顶的累积坡长;Desmet和Govers提出用单位汇水面积近似等于栅格单元坡长的累计流量坡长计算法,,对坡长因子改进,让坡长因子反映了二维水流特征,然后通过提取的坡长因子最终计算出坡长;Moore的基于水流强度的计算法,计算坡长坡度的合成因子(USLE中的LS因子),认为LS因子是地表径流输沙能力的度量,从而将代表地表曲面形态的LS因子的计算解译为流量和坡度呈非线性函数关系的无量纲输沙能力指数的计算;汤国安等[6]提出了坡长的山顶距离算法,这是一种坡长的快速近似计算方法。该方法假定山脊线与水流方向相垂直,并且认为坡长是栅格DEM中的每一个格网,沿着坡面逆流而上,到最近的分水线的垂直距离。这种方法首先是基于水流方向与山脊线垂直的假设,然而实际地表中,河流往往并不是与沿着与山脊线垂直的方向,这种方向的科学性有待进一步检验。目前国内外提取坡长的方法使用最多的是Hickey和Desmet的方法。这两种方法的数据源均是栅格DEM,操作简单,精度较高。
2 坡长的不同算法
2.1 坡长计算一般流程
分布式土壤侵蚀坡长的计算都是模拟地表的水流路径,因此要求DEM表面的水流都存在一个汇聚点或出口。但是DEM数据一般都存在洼地,洼地是被较高高程所包围的DEM局部地形单元,存在与各种结构的DEM中,在自然状态下,洼地多出现在地势平坦的冲积平原上,呈较大面积分布,在地势起伏较大的区域出现的频率并不高。在DEM数据中所表现的洼地,大多是由于数据获取和内插处理时的误差造成的,称为“伪洼地”。洼地的存在会影响水的流动路径,使水流路径到达不了出口。因此在确定水使水流路径畅通无阻。DEM中的闭合洼地和平坦区域可能是真实的地形,但更经常是由于输入资料误差、内插方法以及DEM垂直和水平分辨率等原因造成的。应当进行专门的处理才能使DEM表面的地表径流的流向得以确定。其次要形成地面某点的水流路径,还要确定该点的水流方向,水流方向即某一点的坡向。在此基础上,方可计算坡长。
2.2 径流流向算法
2.2.1 单流向算法
单流向法认为栅格DEM中,中心格网的水流仅仅流入周围八个网格中的一个,也就是说上游累积的径流只会流向下坡方向中的一个栅格单元,并且由于上游来水只会流入确定的一个栅格,所以不需要进行流量的分配。D8算法是应用最普遍的单流向算法,且它已集成在ARCGIS软件中,此外还有Rho8方法。其中,D8算法的流向确定,是通过3×3的DEM网格上,分析中心格网与周围8个栅格单元的最大坡降,从而径流方向只在间隔45°的8个方向中。这种算法是对自然界径流的理想化概况,同时将径流简化为一维的线条,但是这种方法忽略了径流的二维属性。Rho8法是D8法的统计版本,是为克服D8法的平行流向而提出的,Rho8法根据中心栅格单元所在表面的坡向来判断流向,该方法假定水流方向是随机的。
2.2.2 多流向算法
多流向算法有DEMON(Digital Elevation Model Networks)法、D∞算法等。其中,DEMON法,认为DEM表面径流是二维的,水流源点是一个栅格表面,并且径流是有宽度的,而且这个宽度也是可变的。所以该方法更为全面地模拟了地表径流的实际情况。D∞算法是1997年Tarboton[7]提出的D∞算法是以单元格网为中心,每隔45°划分为一个象限,在总共的8个象限中分别计算该象限内的最大坡度和坡向,然后选择坡度最大的象限,并将水流分解为2个方向,使其分别流入该象限内的对角线单元格和水平或垂直方向的单元格,而流量的分配比率则由坡向与水平或垂直方向的夹角以及坡向与对角线方向夹角的比例确定。如图1a,1b,1c。
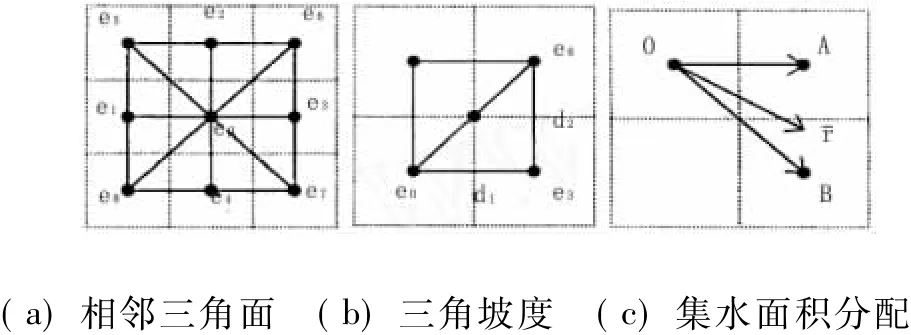
图1 D∞算法的单元格网示意图
2.3 各种流向算法汇水面积的对比分析
汇水面积(Catchment Area)指径流流经一段等高线的上游所有地形的投影面积。汇水面积描述了地表径流流经给定等高线长度上游所经过的区域,也称上游汇水面积(Upslope Catchment Area)或者流量累积值(Flow Accumulation)。并且汇水面积具有这样的特性:位于山脊线上的等高线由于山脊线的分水作用而使其汇水面积比较小,山谷线则由于汇水作用上游汇水面积而具有比较的大的,山坡上的汇水面积值介于二者之间。本研究计算得到了县南沟流域的的各种算法的汇水面积(图2),并对各种流向算法的汇水面积进行统计(表1)。
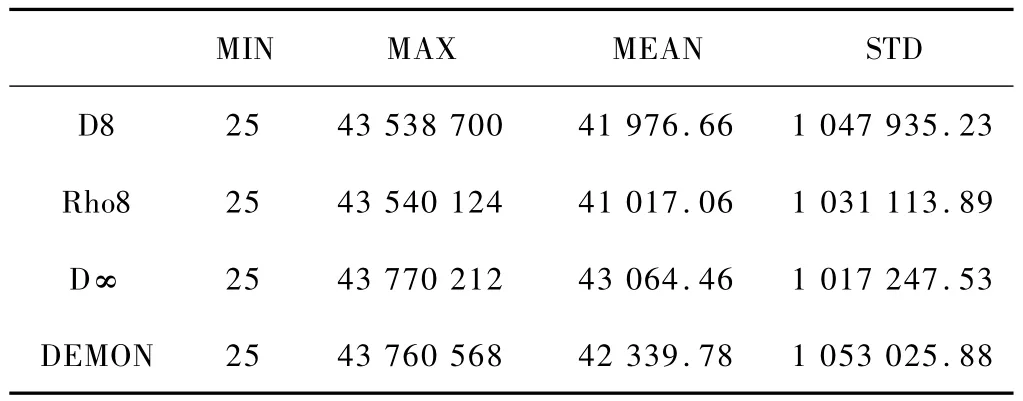
表1 各种流向算法汇水面积的统计值(m2)
由汇水面积的图可以看出:几种流向算法多得的结果存在着显著的差异单流向的算法和多流向算法所得的结果总体的空间格局都符合原理,汇水面积在沟谷地区较大,而在山脊处较小。从图像上,这两种算法对于河网提取较好,然而对于坡面漫流反应较差,与实际情况有很大的差别。多流向算法的汇水面积是平滑且连续的。FMFD算法在沟谷区域生成较宽的水流路径,这是因为FMFD将水量按照坡度贡献分配到它的所有下游栅格,分配的流路增多,汇集的水流面积差别减小,从而相对地增大了流路宽度。

图2 各种算法的汇水面积
3 结语
本研究通过对小流域坡长提取方法的研究,分析和总结前人关于坡长的定义框架,构建坡长的理论体系,为流域坡长计算提供理论基础和技术支持。利用不同流水方向来计算流域坡长,并通过汇水面积比较这些坡长算法,进而分析坡长在小流域的空间分异规律。
基于DEM的小流域坡长的研究和分析为数字地形分析在坡长的研究更为拓宽,也是DEM数字地形分析的数据挖掘的进一步完善和发展。只有将坡长的提取和概念研究好,才能真正为坡长再地学分析、水文分析等领域进行更好的应用。
[1]Horton,R.E.1945.Erosional development of streams and their drainage basins;hydrophysical approach to quantitative morphology.Geological Society of America Bulletin,56(3):275.
[2]Foster,G.,Wischmeier,W.1974.Evaluating irregular slopes for soil loss prediction.
[3]周启明,刘学军.2006.数字地形分析.北京:科学出版社.
[4]Hickey,R.,Smith,A.,Jankowski,P.1994.Slope Length Calculations from a DEM Within ARC/INFO GRID.Computers,environment and urban systems,18(5):365 -380.
[5]Hickey,R.2000.Slope angle and slope length solutions for GIS.Cartography,29(1):1-8.
[6]汤国安,刘学军,间国年.数字高程模型及地学分析的原理与方法[M]:北京:科学出版社.
[7]Tarboton,D.1997.A new method for the determination of flow directions and upslope areas in grid digital elevation models.Water Resources Research,33(2).
