n阶k次幂等矩阵的性质
2011-02-20张绪绪
张绪绪, 刘 青
(1.陕西工业职业技术学院基础部, 陕西 咸阳 712000;2.北京科技大学数理学院, 北京 100083)
0 引 言
矩阵是代数学的一个重要研究对象,也是数学分支不可缺少的工具,矩阵论方法对处理其它各分支问题也相当有力,所以本文在幂等矩阵的基础上定义n阶k次幂等矩阵,并总结出它的一些性质,进而对每个性质给予了必要的证明.下面讨论关于n阶k次幂等矩阵的相关性质.
1 预备知识
性质1(AT)n=(An)T,n∈N*;(A-1)n=(An)-1,n∈N*.
定义1若存在可逆矩阵P,使得P-1BP,则A与B相似.
定义2设A是n阶矩阵,若存在最小正整数k∈N-{0,1},使得Ak=A,则称A为n阶k次幂等矩阵.以下简称k次幂等矩阵.
3 n阶k次幂等矩阵的性质
性质2k次幂等矩阵的转置是k次幂等矩阵.
证明设A是k次幂等矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A,则
(AT)k=(Ak)T=AT
假设存在m∈N-{0,1}且m 性质3k次幂等矩阵的l(l∈N)次幂是p(p∈N-{0,1})且p≤k)次幂等矩阵. 证明设A是k次幂等矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A,则(Al)k=(Ak)l=Al,由最小数原理可知,一定存在p∈N-{0,1}且p≤k,使得(Al)p=Al.因此Al是p次幂等矩阵. 性质4[3]k次幂等矩阵的特征值为0和k-1次单位根. 证明设A是k次幂等矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A. 设λ是A的任意一个特征值,α是A的属于特征值λ的一个特征向量,因而有α≠0且λα=Aα,由于Ak=A,则Akα=Ak-1(Aα)=Ak-1λα=…=λkα,即λkα=Akα=Aα=λα因为α≠0,所以λk=λ,即λ=0或λk-1=1,因此,A的特征值为0和k-1次单位根. 性质5k次幂等正交矩阵的k-1次是单位矩阵. 证明设A为k次幂等矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A,由A是正交矩阵知AAT=E(AT为A的转置矩阵,E为单位矩阵)则 E=AAT=AkAT=Ak-1AAT=Ak-1E 即Ak-1=E,因此,n阶k次幂等正交矩阵A的k-1次幂是单位矩阵. 性质6设A,B同为k次幂等矩阵且可交换,则AB是p(p∈N-{0,1}用p≤k)次幂等矩阵. 证明因为A,B同为k次幂等矩阵,所以存在最小正整数k∈N-{0,1},使得 Ak=A,Bk=B 又因为A与B可交换,则AB=BA,(AB)k=AkBk=AB. 根据最小数原理知,存在最小正整数p∈N-{0,1}且p≤k,使得(AB)p=AB 因此,AB是p(p∈N-{0,1}且p≤k)次幂等矩阵.命题得证. 推论1设A,B同为k次幂等矩阵且可交换,同时AB=O(O表示零矩阵),那么A+B为p(p∈N-{0,1}且p≤k)次幂等矩阵. 证明根据性质3.5可证;也可根据定义证明,因为A,B同为k次幂等矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A,Bk=B,又A,B可交换,知AB=BA=O,因而有 由最小数原理知,存在最小正整数p∈N-{0,1}且p≤k,使得(A+B)p=A+B,因而A+B为p次幂等矩阵. 性质7若A为k次幂等正交矩阵[5],则AT=Ak-2. 证明由A为正交矩阵知,AAT=ATA=E,那么矩阵A可逆,即 A-1=AT 又A为k次幂等矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A.因而有 Ak-2=Ak-1A-1=AkA-1A-1=AA-1A-1=A-1=AT 因此AT=Ak-2,命题得证. 性质8与k次幂等矩阵相似[6]的矩阵仍为k次幂等矩阵. 证明设A是k次幂等矩阵,B是与A相似的矩阵,则存在最小正整数k∈N-{0,1},使得Ak=A.又由于B与A相似,则存在n阶可逆矩阵Q,使得B=Q-1AQ[4],则 Bk=Q-1AkQ=Q-1AQ=B 假设存在m∈N-{0,1}且m 性质9[7]若A为k次幂等矩阵,且A与对角矩阵B相似,则B的对角线上元素为0或k-1次单位根. 证明由A是实对称矩阵知,存在正交矩阵p,使 性质11若A,B均为数域F上的n阶矩阵,如果ABl-1=A(l∈N-{0,1})且BAk-1=B(k∈N-{0,1}),则A是p(p∈N-{0,1}且p≤k)次幂等矩阵,B是q(q∈N-{0,1}且q≤l)次幂等矩阵. 证明因为ABl-1=A且BAk-1=B,则 ABl-1Ak-1=(ABl-1)Ak-1=Ak,ABl-1Ak-1=(ABl-2)(BAk-1)=ABl-1=A 因此Ak=A.根据最小数原理知,存在最小正整数p∈N-{0,1}且p≤k,使得Ap=A.故A是p次幂等矩阵.同理BAk-1Bl-1=(BAk-1)Bl-1=Bl,BAk-1Bl-1=(BAk-2)(ABl-1)=BAk-1=B,因此Bl=B,根据最小数原理知,存在最小正整数q∈N-{0,1}且q≤l,使得Bq=B,故B是q次幂等矩阵.命题得证. 性质12[8]若A是k次幂等矩阵,R(A)是矩阵A的值域,则Ak-1x=x的充要条件是x∈R(Ak-1). 证明必要性 设x∈Fn(数域F上所有n×1阶矩阵组成的集合)满足Ak-1x=x,则必有x∈R(Ak-1). 充分性Ak=A,若x∈R(Ak-1),则必存在y∈Fn,使得Ak-1y=x.于是Ak-1x=Ak-1(Ak-1y)=Ak-2(Aky)=Ak-2Ay=x,从而命题得证. 性质13设A是k次幂等矩阵,B是l次幂等矩阵,证明 ⑴A与B有相同的值域当且仅当Ak-1B=B,Bl-1A=A. ⑵A与B有相同的核当且仅当ABl-1=A,BAk-1=B. 证明⑴必要性 若AV=BV(V表示数域F上的一个向量空间),则对于∀β∈V,Bβ∈AV,即存在α∈V,使得Bβ=Aα,又A是k次幂等矩阵, 则存在最小正整数k∈N-{0,1},使得Ak=A.因而(Ak-1B)β=Ak-1(Bβ)=Ak-1Aα=Akα=Aα=Bβ,由β的任意性得知Ak-1B=B.同理Bl-1A=A. 充分性 由于Ak-1B=B,则BV=(Ak-1B)V=A(Ak-2B)V⊂AV.同理AV⊂BV,所以,AV=BV. ⑵必要性 因为B是l次幂等矩阵,则存在最小正整数l∈N-{0,1},使得Bl=B.那么Bl-B=B(Bl-1-E)=O(O表示零矩阵),则对于∀α∈V,有B[(Bl-1-E)α]=0(0表示列向量),即(Bl-1-E)α∈B-1(0),又A-1(0)=B-1(0),则(Bl-1-E)α∈A-1(0),即[A(Bl-1-E)]α=(ABl-1-A)α=0.再根据α的任意性得,ABl-1=A.同理BAk-1=B. 充分性 若ABl-1=A,则对于∀α∈V,(ABl-1-A)α=[A(Bl-1-E)]α=A[(Bl-1-E)α]=0. 即(Bl-1-E)α∈A-1(0),又因为B[(Bl-1-E)α]=(Bl-B)α=0,即(Bl-1-E)α∈B-1(0)再根据α的任意性有A-1(0)⊆B-1(0).同理可证B-1(0)⊆A-1(0),因此A-1(0)=B-1(0).命题得证. 性质14[8]任意一个n阶矩阵A都可以分解成一个n阶可逆矩阵与一个2次幂等矩阵的乘积. 性质15设A是非零n阶k次幂等正交矩阵,m≠0,n≠0,mAk-1+nEn可逆的充要条件是m+n≠0. 证明充分性 若m+n≠0,则|(m+n)En|≠0,即(m+n)En可逆.又因为n阶k阶次幂等正交矩阵的k-1次幂是单位矩阵,即Ak-1=En,则有 mAk-1+nEn=mEn+nEn=(m+n)En 因此,mAk-1+nEn可逆. 必要性 因为A是非零n阶k次幂等正交矩阵,则Ak-1=En,又因为mAk-1+nEn=mEn+nEn=(m+n)En.若mAk-1+nEn可逆,m≠0且n≠0,则(m+n)En可逆,因此m+n≠0.综上命题成立. 根据最小数原理知,存在最小正整数p∈N-{0,1}且p≤m,使得 证明由已知知,存在最小正整数m∈N-{0,1},使得 根据最小数原理知,存在最小正整数p∈N-{0,1}且p≤m,使得 性质17设A为非零k次幂等矩阵,则A的全体实系数多项式构成实数域上的不超过k维的线性空间[10]. 证明因为A为非零k次幂等矩阵,即存在最小正整数k∈N-{0,1},使得Ak=A.所以A的实系数多项式的一般表达式为f(A)=a1Ak-1+…+ak-2A2+ak-1A+akE. 显然f(A)可以用E,A,A2,…,Ak-1线性表示出.又因为E,A,A2,…,Ak-1的秩小于等于k,故A的全体实系数多项式构成实数域上的不超过k维的线性空间. 推论3若A为可逆k次幂等矩阵,则A的全体实系数多项式构成实数域上的不超过k-1维线性空间. 证明因为A为可逆k次幂等矩阵,由性质3.5知,Ak-1=E(k∈N-{0,1}),那么E,A,A2,…,Ak-1等价于E,A,A2,…,Ak-2.又因为E,A,A2,…,Ak-2的秩小于等于k-1,故A的全体实系数多项式构成实数域上的不超过k-1维的线性空间. 本文在幂等矩阵的有关概念与性质的基础上,把一般矩阵的性质推广到特殊的n阶k次幂等矩阵,极大的丰富了代数这门课的内涵,推广了幂等矩阵研究的相关理论.至于这种推广的理论与实际应用价值怎样,它对其它科学研究将产生何种影响,还有待科研工作者进一步探索与发掘. 参考文献 [1] 张禾瑞,郝鈵新.高等代数(第四版)[M].北京:高等教育出版社,2003. [2] 倪国熙.常用的矩阵理论和方法[M].上海:上海科学技术出版社.1984. [3] 杨 洪,宋千红.关于幂等矩阵的几个性质[J].黑龙江八一龙垦大学学报,2009,8(3):84-87. [4] 刘道建.矩阵及其性质[J].湘潭师范学院学报,2005,24(5):45-48. [5] 陈公宁.矩阵理论与应用[M].北京:科学出版社,2007. [6] 史荣昌,魏 丰.矩阵分析[M].北京:北京理工大学出版社,2005. [7] 郭 华.实幂等矩阵的几个等价条件[J].渝州大学学报,2001,18(2):20-23. [8] 杨闻起.k次幂等变换与k次幂等矩阵[J].宝鸡文理学院学报(自然科学版), 2008,28(4):261-262. [9] Roger A.Horn,Charles R.Johnson.Matrix Analysis[M].China:Machine Press,2005,(2):3-8. [10] 朱 敏.一类常见矩阵的性质[J].巢湖学院院报,2002,4(3):6-7.





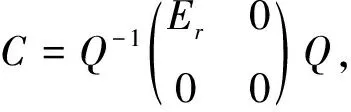



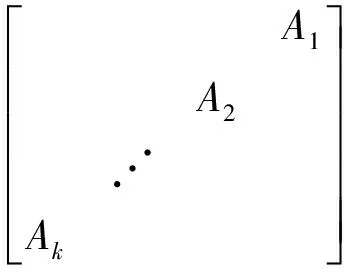


4 结束语
