ARIMA模型在贸易规模预测中的适用性
——基于中国服务贸易进出口规模的分析
2011-02-20刘翔
刘 翔
(上海交通大学安泰经济与管理学院, 上海 200052)
0 前言
ARIMA模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),是由博克思(Box)和詹金斯(Jenkins)于20世纪70年代初提出的著名时间序列预测方法,又被称为Box-Jenkins模型或博克思-詹金斯法[1].其基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列,并认为该序列蕴含的规律还将持续遵循下去.这个模型一旦被识别后就可以从时间序列的过去值及现在值进行外推预测未来值.因此,ARIMA模型在实证研究中被广泛运用于时间序列分析和模型预测领域.
1 ARIMA模型的类型及构建过程
ARIMA模型建模的对象是平稳的时间序列,因此在对一个离散的单变量时间序列进行建模分析时,应当首先考察其平稳性,再分析和判断数据序列的生成过程.
根据平稳时间序列生成机制的不同,ARIMA模型实际包含3种类型的模型[2]:
(1)自回归模型(简称AR模型): 模型为p阶自回归过程,简记为AR(p),用公式表示为
yt=φ1yt-1+φ2yt-2+…+φpyt-p+at
其中,{at}是满足0均值和常数方差的白噪声序列,φi为模型的待估参数.
(2)移动平均模型(简称MA模型):
模型为q阶移动平均过程,简记为MA(q),用公式表示为
yt=at-θ1at-1-θ2at-2-…-θqat-q
其中,θi为模型的待估参数,其它字母含义同上.
(3)自回归移动平均混合模型(简称ARMA模型)
模型为自回归移动平均混合过程,简记为ARMA(p,q),用公式表示为
yt=φ1yt-1+φ2yt-2+…+φpyt-p+at-θ1at-1-θ2at-2-…-θqat-q
其中,字母含义同上.可以看到,ARIMA模型为自回归AR模型和移动平均MA模型的算数和,其中的I表示差分的逆运算.
对于一个时间序列{yt}而言,构建ARIMA模型的一般步骤为:
首先进行单位根检验或游程检验其平稳性,若非平稳后通过d阶差分作平稳化处理;如果数据存在异方差,则需对数据进行技术处理,直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零.
之后通过时间序列模型的识别规则判断序列所属类型并建立模型.若平稳序列的偏相关函数是截尾的,而自相关函数是拖尾的,适合AR模型;若平稳序列的偏相关函数是拖尾的,而自相关函数是截尾的,适合MA模型;若平稳序列的偏相关函数和自相关函数均是拖尾的,则序列适合ARMA模型[3].
然后对该平稳时间序列建立相应的ARMA(p,q)模型,确定后的差分自回归移动平均模型整体表示为ARIMA(p,d,q),其中p为自回归项,q为移动平均项数,d为时间序列成为平稳时所做的差分次数.
最后对模型进行参数估计并检验参数是否具有统计意义,如有必要还需要进行假设检验,诊断残差序列是否为白噪声.
以上步骤进行完后,获得与该时间序列匹配的ARIMA模型,并可以通过模型进行趋势预测.
ARIMA模型在宏观经济领域有很多重要的运用,通常基于历史数据构建模型,并在置信区间内对所分析经济对象的趋势进行判断.本文将以中国服务贸易进出口规模为分析对象,探讨ARIMA这一模型工具的适用性.
2 中国服务贸易进出口规模模型的构建和预测
2.1 服务贸易研究背景介绍
服务贸易作为一种新兴的贸易形式,在一定程度上代表了国家的经济发展水平.通常情况下,发达国家服务贸易在该国国际贸易中比重较大.多年以来我国利用对外贸易带动经济长期增长,货物贸易起着主导作用,而与之相对应的服务贸易却始终为逆差状态.但不可否认服务贸易已经成为我国经济新的增长点,从1982年到2010年,我国服务贸易规模的年均增长速度达到17%[4].目前我国面临着产业结构调整的转型困难,而大力发展服务业及服务跨国贸易是扭转这一局面、实现经济成功转型的突破点之一.
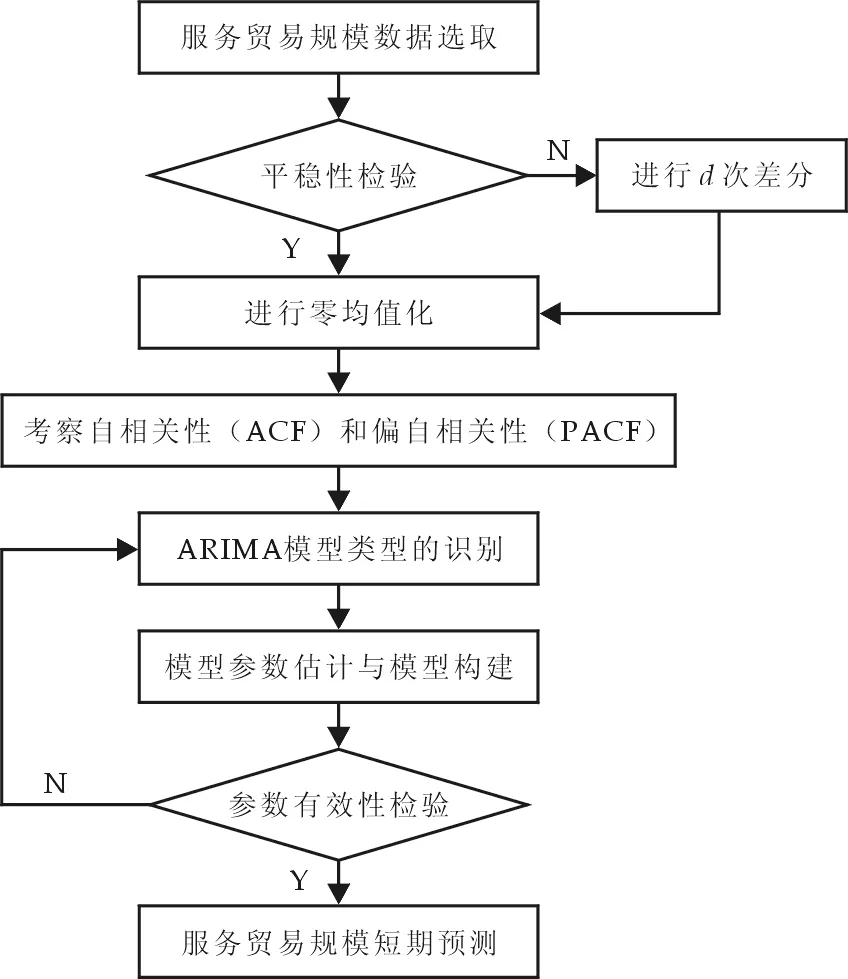
图1 我国服务贸易规模ARIMA模型预测的基本流程
虽然服务贸易逆差在逐步缩小,但是由于受到越来越多不可控的国际因素的影响,目前我国服务贸易的增长呈现较大的波动性.因此,全面把握我国服务贸易的发展规律和未来走势对于我国采取有利措施、保证服务贸易的持续稳定发展具有重要的意义.为此,本文采用时间序列分析方法,从数量建模的角度揭示我国服务贸易的发展规律,重点探讨ARIMA模型对贸易规模预测的适用程度.
根据建立ARIMA(p,d,q)模型的要点,我国服务贸易规模预测的基本流程如图1所示.
2.2 数据选取
我国从1982年起正式将服务贸易纳入商务和海关统计的范围[5],本研究选取数据来源于国家统计局2011年出版的《中国统计年鉴(2010)》及中国商务部《中国服务贸易统计(2010)》提供的服务贸易数据.为检验模型的后验性,同时保证足够的样本数量范围,本文选取中国1982~2008年的服务进出口数据作为建模样本,将2009和2010年贸易数据作为后验样本来判断模型估计的有效性.本文将我国服务贸易进口额时间序列简记为M,出口额时间序列简记为X,进出口总额时间序列简记为MX.
2.3 数据平稳性检验及处理
从图2的服务贸易总额MX时间路径中可以看出,原数据序列MX有着明显的指数增长趋势(图1a),为非平稳序列.通过对数处理后,对数序列LMX表现为线性增长趋势.为从统计意义上对序列的平稳性进行识别,对数据序列进行单位根ADF检验.ADF检验显示对数序列LMX的t统计量的显著性概率P=0.988,远大于α=0.05,接受零假设,即序列显著存在单位根.
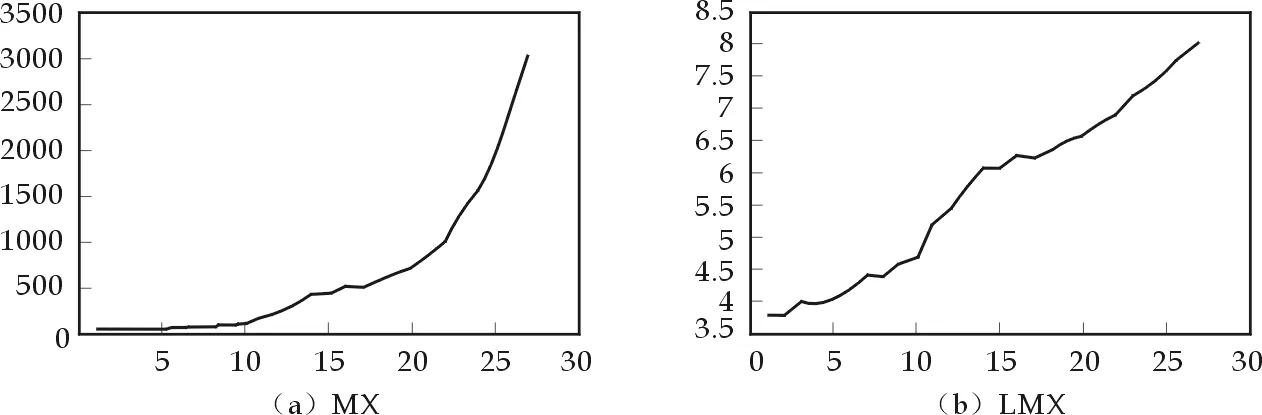
图2 服务贸易总额及其对数序列的时间路径
为消除单位根的影响,对序列LMX进行差分运算,记为ΔLMX,再进行平稳性ADF检验.检验结果表明LMX一阶差分序列单位根仍存在,二阶差分(序列记为Δ2LMX)后单位根不存在,时间序列为平稳序列,即服务贸易总额对数序列LMX为二阶单整序列.
2.4 数据拟合与模型的构建
在SAS统计软件中对LMX的二次差分序列Δ2LMX进行自相关(ACF)和偏相关(PACF)分析,结果如图3所示.从图3中可以看出,Δ2LMX的自相关图在一阶处是截尾的,而其对应的偏相关图是拖尾的,依此初步判断序列LMX遵循的模型为ARIMA(0,2,1),属于MA模型类型.
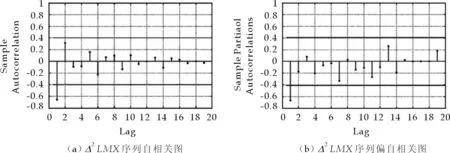
图3 Δ2LMX序列的自相关图和偏相关图
为进一步判断模型类型,结合上述分析,本文分别尝试用ARIMA(0,2,1)、ARIMA(0,2,1)、 ARIMA(1,2,1)、 ARIMA(1,2,2) 以及ARIMA(2,2,1)5个模型对序列LMX进行拟合检验.结果显示,只有ARIMA(0,2,1)和ARIMA(0,2,1)2个模型通过了参数检验,其余模型都存在估计参数检验不显著的情形,验证了我们之前关于序列属于MA类型的判断.两模型的AIC值(赤池信息准则Akaike Information Criterion)和SSR值(剩余平方和)如表1所示.
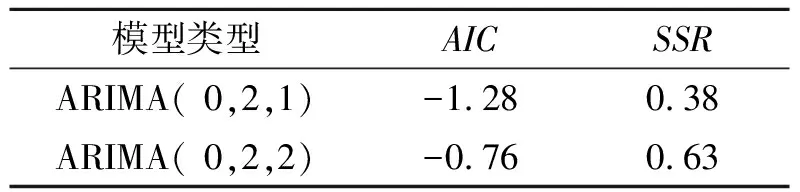
表1 模型估计的AIC值和SSR值
根据表1中模型估计的结果并考虑到建模的简约原则,对贸易总额的对数序列LMX拟采用ARIMA(0,2,1)模型进行估计,其结果通过了模型的残差平稳性检验,表明该模型合理,模型估计结果为:
lnMXt=0.985 8at-1+at
(1)
t值 (-37.325)R2=0.5
为了更全面地对服务贸易规模进行拟合和预测,分析服务贸易进口和出口各自的变化规律,按照上述建模过程,分别对服务贸易进口额时间序列Mt和出口额时间序列Xt建立模型.我国服务贸易进口额Mt合理的ARIMA模型估计结果为:
ΔlnMt=0.195-0.564ΔlnMt-2+0.962at-2+at
(2)
t值 (4.707) (-4.740) (28.578)R2=0.451
同理,我国服务贸易出口额Xt合理的ARIMA模型估计结果为:
Δ2lnXt=-0.826Δ2lnXt-2+0.962at-2+at
(3)
t值 (-10.333) (-20.731)R2=0.545
3 ARIMA模型对服务贸易规模预测的适用性分析
3.1 服务贸易规模短期预测
利用上述建立的模型(1)、(2)和(3)式,分别对我国2009年和2010年服务贸易总额、进口额以及出口额进行外推预测,预测结果如表2所示.
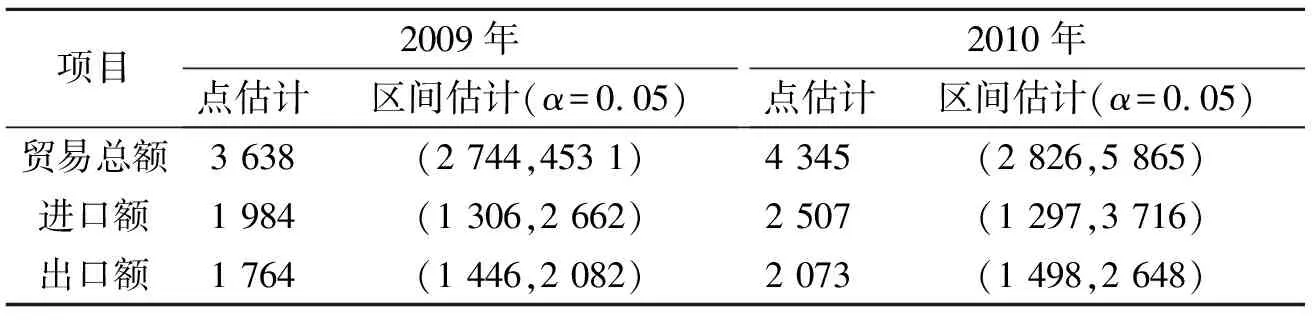
表2 2009~2010年中国服务贸易规模预测(单位:亿美元)
表2表明,2009年和2010年我国的服务贸易总额分别为3 638亿美元和4 345亿美元,年增长率均为19%,而历史数据显示由于服务贸易进口的快速增加,模型根据这一内在规律预测2009年和2010年服务贸易进口增长速度将达到26%的水平.
3.2 数据对比及差异分析
我们结合2009年和2010年的实际数据做一对比(表3),可以发现数据出现了较大的高估,偏差范围为20%~30%.通过数据回溯可以发现,由于全球金融危机对实体经济造成的滞后影响,2009年服务贸易近10年来出现了较大的负增长,较2008年降低了5.8%,服务贸易出口额甚至降低了12.2%.
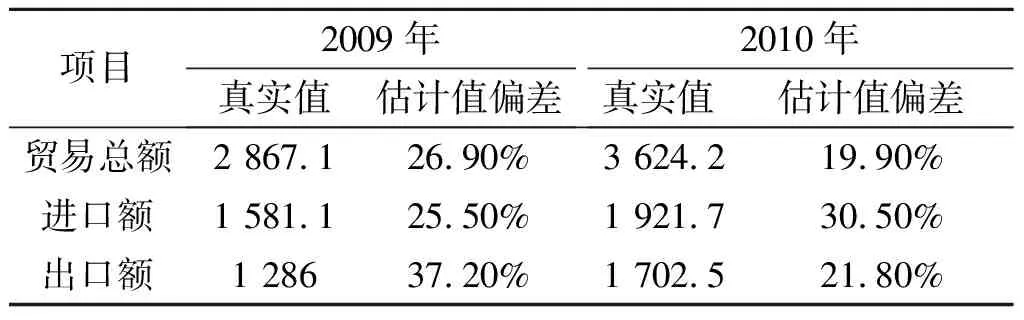
表3 2009~2010年中国服务贸易规模及预测偏差对比(单位:亿美元)
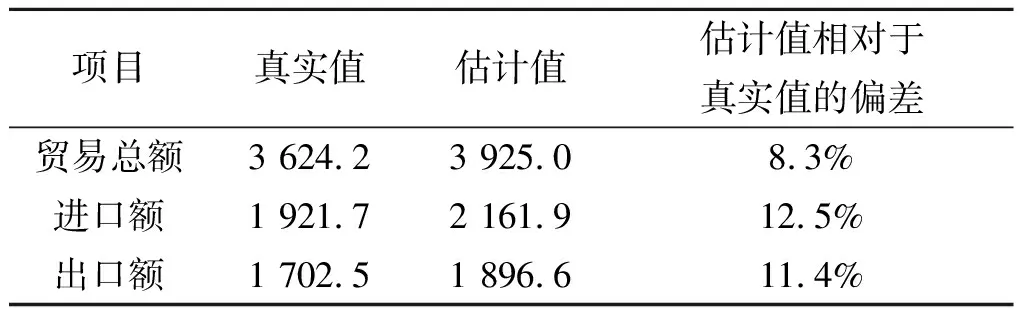
表4 2010年中国服务贸易规模及重估预测偏差对比(单位:亿美元)
我国服务贸易在国际市场上并不具备货物贸易那样的优势,当全球经济处于下滑阶段时,作为幼稚产业并不具备抗击风险的能力,因此偏离模型根据历史数据估计的趋势.但区间估计弥补了点估计的不足,实际值基本上都在区间估计的范围内,考虑到了突发变动对序列趋势的影响.
同时我们也可以看到,随着年份的推移,2010年预测数据的精度相对2009年出现了更大的波动.我们尝试将2009年的数据作为样本构建新的模型,并以新模型来预测2010年的数据,结果如表4所示.
由于考虑了2009年的突变因素,数据序列内在逻辑的变动相应改变了模型参数估计,2010年预测偏差大幅降低,模型的参考价值提高.
4 结束语
模型预测的主要目的是在考虑随机波动的前提下对趋势进行模拟和分析,其预测结果不是为精确到细节,而是作为参考指标和判断依据.从上述构建我国服务贸易进出口规模ARIMA模型并进行短期预测的过程中,模型从动态角度反映出服务贸易规模的变动趋势和特点,我们可以看到ARIMA这个重要的时间序列建模方法适用于很多纵向经济现象的定量分析,特别是经济体规模的变动预测,能够帮助理解和拟合数据内部隐藏的规律性.模型对历史数据中包含信息做了充分吸收,相对于简单的增长率平均法更加科学和有效.同时区间预测与点预测相结合,使得模型预测结果更加客观严谨.
但是从预测的理想程度上,本文也提出利用ARIMA模型进行经济预测时的局限性:
(1)突发事件对数据序列趋势的影响. 应该注意的是ARIMA模型基于的原理是假设序列保持不变的趋势,置信区间虽然已经包含了随机波动的范围,但当出现影响事件发展方向的“黑天鹅”事件时,其预测将偏离真实情况.
(2)区间估计范围过大. 根据本文中的研究样本,在置信度为95%的情况下,区间估计相对于点估计值的变动达到了±20%以上,最高的甚至达到±40%.对于宏观经济变量来说,年增长率10%已经属于较大的变化,因此区间估计范围过大会使预测丧失其意义.
针对以上两个局限性,本文给出如下建议:
(1)时间序列模型应对数据进行适时的动态更新和调整,以便更好地反映和模拟内在规律.
(2)适当降低区间估计的范围,以保证预测本身的价值.由于缩小置信区间会以降低置信水平为代价,因此在构造模型时需要在两者间做一权衡.同时,尽可能扩大样本数量,以保证在置信水平不变的前提下置信区间相对变窄.
参考文献
[1] 王炜炘,杜金观,伍尤桂,等.应用时间序列分析[M]. 桂林:广西师范大学出版社,1999:102-183.
[2] George E. P. Box, Gwilym M.Jenkins. 时间序列分析-预测与控制[M]. 北京:中国统计出版社,1997:101-149.
[3] 张树京,齐立心. 时间序列分析简明教程[M]. 北京:北方交通大学出版社,2003:24-59.
[4]中国商务部. 中国服务贸易(2010)[M]. 北京:中国统计出版社,2011.
[5] 国家统计局. 中国服务贸易(2010)[M]. 北京:中国统计出版社,2011.
[6] 姜 弘. 居民消费价格指数的时间序列分析及预测[J]. 统计与决策,2009,4:26-33.
[7] 谢佳利,杨善朝,梁 鑫.我国CPI时间序列预测模型的比较及实证检验[J]. 统计与决策,2008,6:74-82.
[8] 王振龙. 时间序列分析[M]. 北京:中国统计出版社,2000.
