模糊数学综合评价方法在储层预测中的应用——以鄂尔多斯盆地延长气田东部地区上古生界为例

张 杰， 崔宏俊

(延长油气公司天然气勘探部， 陕西 延安 716000)

图1 鄂尔多斯盆地构造单元划分及研究区位置图 1．研究区边界；2．盆地边界；3．构造单元界限；4．奥陶系气藏；5．石炭-二叠系气藏

0 引 言

延长气田东部地区位于鄂尔多斯盆地的东南部，区域构造上大部分属于陕北斜坡，东部包括晋西挠褶带的西缘部分，面积约1.6×104km2(图1),其中该区上古生界山西组山1段和山2段、石盒子组盒7段及盒8段与石千峰组下部的千5段是研究区主要的含气层系.山西组为发育在浅海陆棚基础上的三角洲沉积，沉积相带呈南北向相带分异的特点.下石盒子组研究区北缘的冲积扇规模逐步扩大，主要发育辫状河三角洲前缘沉积.石千峰组除了发育三角洲沉积外，在研究区西北部还发育滨浅湖沉积[1-3].由于早古生代海侵、海退频繁，晚古生代则湖进、湖退交替进行.沉积环境多变，不同环境沉积体系在纵向上相互叠置，形成了研究区多个不同类型的生储盖组合.因此，对研究区储气层段进行客观、综合性的评价是确定储层储集天然气有利程度的关键，对今后气田的勘探开发具有极大的现实意义.本文采用模糊数学中的模糊综合评判方法对各个层段进行了全面分析，即应用判断矩阵法和加权平均模型计算确定生储盖评价标准，通过综合分析，预测有利生储盖层段.

1 储层特征

上古生界碎屑岩储集层中岩屑含量相对较高，平均为15.6%，砂岩多以岩屑砂岩为主；胶结类型以孔隙式胶结为主；孔隙类型多样，主要为各种次生孔隙；颗粒以山1、山2段最粗，分选中等—好，其中千5、盒8、山2分选较好.孔隙度、渗透率的平均值主要在4%～6%、0.12×10-3～0.2×10-3μm2之间，有单峰、双峰、正态3种分布方式；孔渗相关性较好，相关系数R一般大于0.7；各段毛管压力曲线都为陡斜式.

1.1 储层孔隙类型

根据孔隙成因、几何形状并结合相关试验的孔隙分类方案，研究区上古生界气层主要发育3种孔隙类型(表1).

表1 研究区孔隙类型及特征表

1.2 储层物性特征

研究区物性分析统计结果表明，上古生界气层孔隙度和渗透率值变化大，孔隙度最小为0.34%，最高为18.16%，平均孔隙度为6.19%，绝大多数集中在4%～6%之间；渗透率最小为0.003×10-3μm2，最高为10.17×10-3μm2，平均渗透率为0.32×10-3μm2，绝大多数小于0.1×10-3μm2.物性好的地区主要分布在三角洲前缘水下分流河道砂体较发育的地区.毛管压力曲线形态和参数特征分析表明研究区主要发育低排驱压力-高吼道型、低排驱压力-中吼道型和高排驱压力-低喉道型3种孔隙结构.

2 储层分类评价

影响储层储集油气好坏的因素很多，但对于延长油田东区古生界的储气层中哪些区块有利于天然气富集，哪些区块不利于天然气的富集又有很大的不确定性和模糊性，如何把这些因素有效地统一起来，对储气层段做一个客观的、综合性的评价是确定储层储集天然气有利程度的关键.鉴于此，采用模糊综合评判方法才能准确定量地反映各个区块储层的差别，从而为决策提供可以进行比较和判别的依据.

2.1 模糊综合评判模型的建立

模糊综合评判方法是一种运用模糊变换原理、最大隶属度原则分析和评价模糊系统的方法，同时也是一种以模糊推理为主的定性和定量相结合、精确与非精确相统一的分析评判方法，即在一个要评判的对象集中，根据问题要求，对每一个对象赋予一个非负实数即判别指标，再根据评判指标大小对各对象进行排序，从中评判出最佳者[4,5].

2.1.1 综合评判的数学模型

设所考虑的评价因素集合为：U={U1,U2，…，Um}，式中Ui(1,2,…,m)代表评价因素(以上古生界碎屑岩储层为例).U1-砂层的孔隙度(%)；U2-砂层的渗透率(10-3μm2)；U3-砂层孔喉半径中值(μm)；U4-储层含气饱和度(%)；U5-存储系数(%·m)；U6-渗流系数(10-3μm2·m)；U7-砂层厚度(m)；U8-储层厚度(m)；U9-砂层流动带指数；U10-测井解释成果.

评语集合为：V={V1，V2,…,Vn}，式中Vj(j=1,2,…,n)代表评判级别，n为整数.在具体进行评价时，评语集合V用被评价单井集合代替，即：

V={延101,延102,延103,…,延气4}

设单因素评价矩阵为R=[rij]m×n，其中rij为第i种因素对第j种评语的隶属度，又设单因素集合中各因素的权重A=(a1,a2,…,am)，则模糊综合评判方程为：

B=A∘R

式中：B=(b1,b2,…,bn)，为综合评判结果；∘为模糊运算符号.

2.1.2 建立权重向量

确定权重系数的方法有多种，较常用的有德尔斐法、专家调查法和判断矩阵法.在研究区我们采用了判断矩阵分析法.计算公式如下：

式中fμj(μi)表示因素μi相对于因素μj的重要程度，由m×m个bij可构造判断矩阵为：

根据构造判断矩阵B，计算它的最大特征根及特征向量：

ξ=(X1,X2,…,Xm)

取Xi作为因素μi的重要程度系数ai，即：

A=(X1,X2,…,Xm)=(a1,a2,…,am)

2.1.3 模型计算

模糊综合评判的计算模型有多种，最常用的主要有3种:(1)主因素决定型；(2)主因素突出型；(3)加权平均型.在储层综合评价中，采用加权平均型进行计算，即：

2.1.4 综合评判

综合评判的最终结果是一个模糊子集：

B=[b1,b2,…,bn]

表2 延长气田东区储层综合评价标准

其中bj为所研究储层对等级Vj的隶属度，采用最大隶属度判别准则对储层进行综合评价，即B值越大，储层越有利.

2.2 上古生界有利储层综合评价

根据上述分析，建立了模糊评价隶属度标准(表2)，在此基础上建立了单因素评价矩阵,结合研究区的实际情况，建立评价标准(表2).

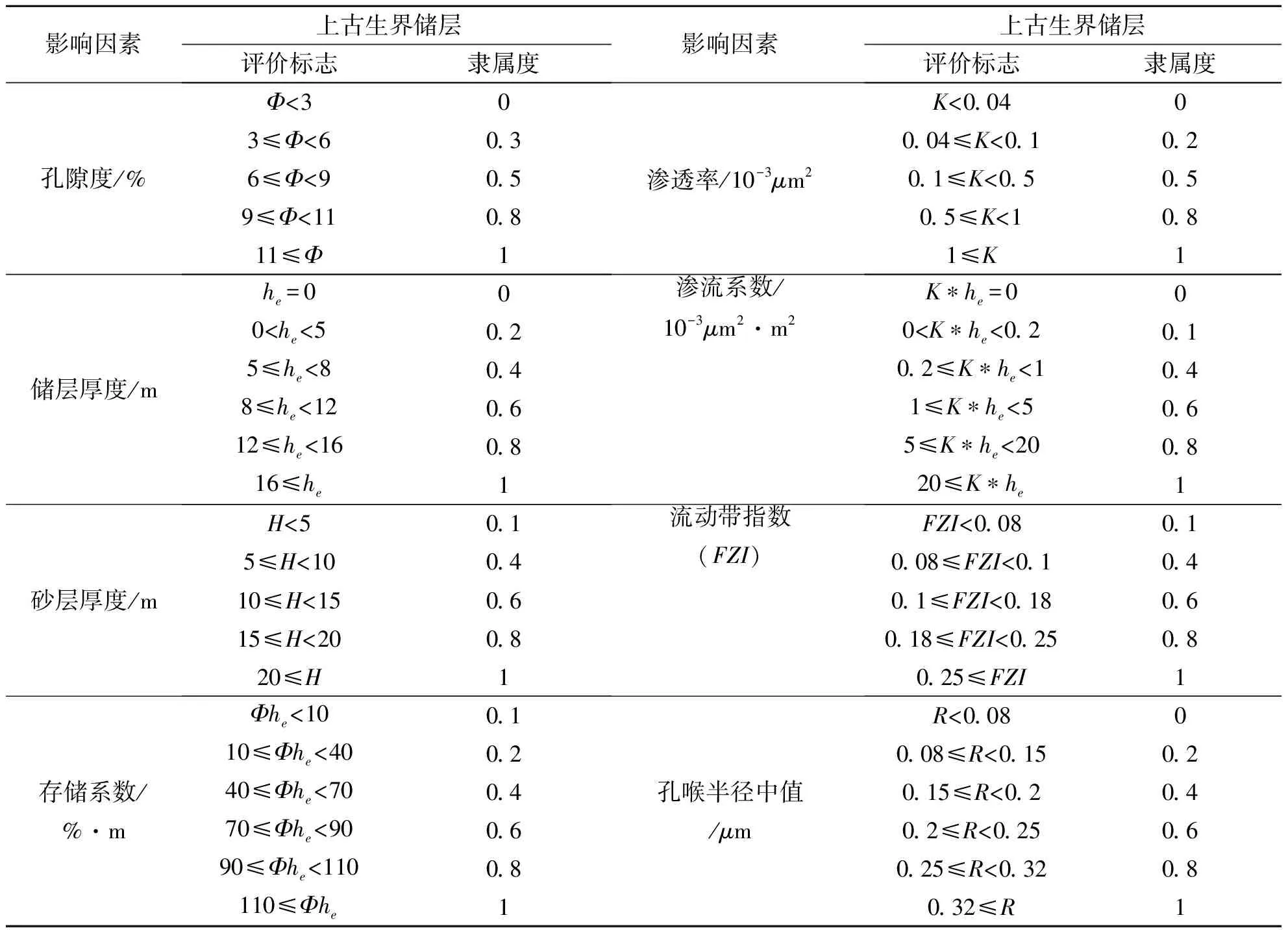
表3 延长气田东区上古生界有利储层模糊综合评判隶属度表

表4 研究区上古生界储层模糊数学综合评价(B值)

3 结束语

本文建立了碎屑岩生储盖组合模糊评价隶属度标准(表3)，在此基础上得到了单因素评价矩阵，沿用此评价标准，经过加权平均模型的计算最终得到了综合评判的模糊子集.

通过生储盖组合综合评价B值得出古生界各储集层段中盒8段、山1段、山2段为最有利(表4).

参考文献

[1] 陈孟晋,汪泽成鄂尔多斯盆地南部晚古生代沉积特征与天然气勘探潜力[J]. 石油与天然气地质，2006,33(1):1-5.

[2] 陈全红.鄂尔多斯盆地上古生界沉积体系及油气富集规律研究[D]. 西安:西北大学硕士学位论文,2007.

[3] 陈洪德,侯建中,田景春，等.鄂尔多斯盆地晚古生代沉积层序地层学与盆地构造演化研究[J].矿物岩石,2001,21(3):16-22.

[4] 曾允孚,夏文杰.沉积岩石学[M]. 北京:地质大学出版社,1986:194-199.

[5] 祝国瑞,张根寿.地图分析[M]. 北京:北京测绘出版社,1994:246-252.