基于非合作博弈的企业知识网络形成研究

汤 婧， 韩丽川

(上海交通大学安泰经济与管理学院， 上海 200052)

0 引 言

知识网络是知识参与者的一种社会网络，能够实现个人、团体、组织与内部等层次上的知识创造与传递[1].知识网络的形成与演化是一个动态的过程，网络的状态会随着时间的推移而发生变化，这种变化包括不同节点之间连接的变化以及在此基础上产生的网络特征的变化.知识网络中，以知识共享、知识转移、知识创新等知识活动为主导的合作行为可使节点获得更大的收益，参与方为了实现利益最大化而选择与其他的参与方形成连接，从而导致网络状态的变化，这些行动的重复就形成了动态演化的知识网络.

在网络形成的研究中，博弈论是一个重要的研究工具.在运用博弈论对网络形成理论的研究中，Aderlini & Lanni(1996)以及Goyal & Janssen(1997)揭示了网络结构影响企业间协调的机制；Bala & Goyal(2002)用非合作博弈理论研究了单向流网络及双相流网络的形成模型及稳定性[2]；Jackson & Wolinsky(1996)通过建立静态模型，对网络形成与网络结构进行了分析，得出了有效网络的结论[3]；谢逢洁与崔文田(2008)对Jackson & Wolinsky的模型进行了进一步深入研究，探讨个体异质因素对有效网络结构的影响[4].这些网络形成理论为本文探讨知识网络的形成提供了一个很好的理论基础.在资源有效性的前提下，我们认为企业投入知识资源越多，获得的经济效益越多.但是，当我们不再将企业看作是孤立的个体，而形成了特定的网络结构时，网络结构对企业投入知识资源所获得的均衡利润会产生怎样的影响，这一问题直接关系到企业投入知识资源的有效策略，也是本文研究的一个重点.因此，本文在网络形成理论的基础上构建了一个以企业为节点的知识网络形成的两阶段模型，重点讨论了N个企业知识参与者在不同知识转移系数及知识投入量的前提下所形成的有效网络结构，并进一步探讨了不同网络结构对古诺均衡利润的影响，旨在探讨企业知识网络的形成以及网络的形成对参与企业的行为的经济学效益的影响.

1 基本模型定义

现在研究一个以n个同质企业为节点的以知识创新为目标的网络，网络持续t个时间段.网络中的企业生产同一种产品，面临着一个线性的反需求函数:

假设1：节点间的知识资源是互补的，每个节点均拥有自己的最佳优势.

假设2：t阶段节点企业之间进行知识合作时，仅对t阶段投入的知识资源量完全开放.

下面对模型中的定义进行说明：

定义1：网络gt={N,L}，N={1,2,…,n}是节点的集合，L是节点连接所形成的边的集合.如果两个节点之间形成知识合作关系，则形成了两节点之间的边.

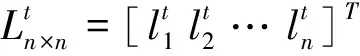
2 两阶段模型分析

2.1 知识网络形成阶段

初始t=0阶段，g0是一个空网，Ln×n=0，对节点企业i而言，其决策目标为：

借助古诺模型的博弈均衡进行求解，在古诺模型中，通过一阶最优化条件进行求解可得t=0阶段节点i的均衡产量与均衡利润：

t=0以后的时间段，节点企业不再独立地进行知识活动，而是可以选择与其他节点建立知识合作关系，进行知识共享，形成节点与节点之间的连接.通过知识合作活动，节点企业可以吸收转化其他节点的知识，用于本企业的知识创新.伴随着知识活动的发生，节点企业初始状态下的知识存量、单位成本、均衡产量以及均衡利润都在发生着变化.

随着知识网络的动态演化，参与人的知识存量随着知识合作行为的发生而不断发生变化.我们首先建立知识存量的状态转移方程，令

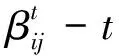
每一阶段企业知识资源的投入除了对企业知识存量产生影响之外，还能够降低企业的单位成本.单位成本的变化满足以下等式：

上式反映了企业的单位成本随着新知识的投入而降低，而降低的幅度取决于企业投入的知识资源量.每一时间段中，企业投入得越多，单位成本随之降低的幅度越大，如果投入的知识为零，则单位产品降低的幅度为零.随着时间的推移以及新知识的不断获得和增加,单位产品成本的降低幅度也越来越大，但成本不可能完全消除，降低为零.单位成本降低函数满足以下假设[6]：

至此，我们分别建立了随着时间的推移知识存量的增加函数以及单位成本的降低函数.本文考虑以下两个阶段的博弈过程, 在每个时期的第一阶段知识网络形成阶段,n个节点企业与其他的节点形成连接，进行知识合作活动.在这个过程中，知识网络形成一定的网络结构，通过知识投入降低单位成本; 第二阶段产出阶段,n个节点企业在给定第一阶段的知识网络结构后, 在产品市场上进行古诺竞争，选择各自产出使自己的利润最大化.整个博弈过程是一个非合作的动态博弈.

在本模型的知识网络中，节点可以与自己有连接的节点进行直接知识合作活动, 也可以通过这些直接连接和那些与自己有间接连接的个体进行知识合作活动，直接连接关系和间接连接关系都可以产生收益.区别在于，直接连接需要一定的成本, 间接连接不需要成本但获得的收益随间接连接最短路径距离的增大而降低.

首先考虑第一阶段，即知识网络形成阶段博弈.对于n个节点的知识网络，此时，不仅有直接连接形成带来的收益，还有间接连接带来的收益，节点i的网络连接的效用函数:

根据Jackson & Wolinsky(1996)以及谢逢洁与崔文田(2008)中的有效网络结构定理[3,4]，加入知识网络的知识转移效率以及知识资源量这两个变量，以下对知识网络的动态形成作进一步探讨.

在星型结构下，要保证U(g*)>0,即须满足

在这种情形下，任意网络结构下，网络的总效用U(g)都是负的，而空图的网络效用为0.因此，t阶段的知识网络为孤立的点.在知识网络形成初期，即t=1时，存在连接成本系数c过高，知识网络无法形成的可能性.

至此，我们得到了给定t阶段知识转移系数δt、知识资源向量et以及连接成本c，我们得到了第一阶段形成的有效的网络结构，每一个节点企业在进行知识合作后都投入了大于或者等于t阶段自身投入的知识资源量.在第一阶段给定的网络结构下，我们讨论第二个生产阶段节点企业的古诺均衡产量及均衡利润.

2.2 古诺博弈阶段

在古诺博弈阶段，我们在知识网络形成阶段的基础上，通过古诺博弈进一步分析网络形成对参与企业的行为的经济学效益的影响.

考虑到知识资源的投入，设知识资源的单位成本为v，则t=m阶段节点企业i的利润函数为：

通过古诺模型的均衡博弈，t=m阶段节点i的均衡产量和均衡利润同理可得：

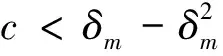
有效网络结构为全连接的蛛网型结构.此时，对任意节点企业i而言：

从上式可以看出，知识转移系数与节点的知识贡献量对均衡利润的边际影响是负相关的.在全连接的蛛网型网络结构中，节点企业在该阶段通过自身投入及知识转移获得的知识资源量是各种网络结构中最大的，但是由于这种结构下受到知识转移系数的影响较大，因此对均衡利润边际影响的递减作用也是最大的.

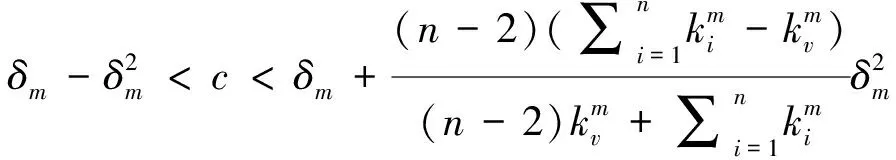
对于边缘节点i,i≠w而言

中心位置的节点在该阶段通过自身投入和知识转移获得知识资源量较大，但是知识转移系数所产生的知识资源量对均衡利润的边际影响的递减作用较大.而边缘位置的节点在该阶段通过自身投入和知识转移获得知识资源量较小，但是知识转移系数所产生的知识资源量对均衡利润的边际影响的递减作用较小.

给定其他节点投入的知识资源量，对于单个节点企业而言，节点阶段投入的知识资源量对均衡利润的影响是正相关的，由于节点之间不存在知识转移，该阶段节点企业获得的知识资源量相比其他网络结构是最小的，但是由于没有网络结构因素的影响，因此自身投入的知识资源量对均衡利润的边际影响最大.

3 结束语

本文假设一个以n个同质企业为节点的网络，对该网络构造了一个两阶段的博弈模型，该模型引入了知识转移系数.在第一阶段知识网络形成博弈中，探讨了不同的情形下形成的有效网络结构.在第二阶段古诺均衡博弈中，进一步探讨了不同网络结构下节点企业的知识贡献量对古诺均衡利润的边际影响的不同.分析表明，给定相同的知识资源向量，通过节点之间的知识转移，在不同网络结构下，节点企业获得的知识资源量是不同的.同时，网络结构因素会对自身投入的知识资源量对均衡利润的边际影响产生递减作用，这种递减作用的程度在不同的网络结构下也有所区别.

需要指出的是，为了简化模型，本文没有考虑节点的知识吸收能力等内生变量对知识网络形成的影响，并且假设了节点在每一时间段仅对特定的知识资源进行开放，如果进一步放开限定条件，更全面的考虑知识网络形成的内生变量，模型需要作进一步的探讨.

参考文献

[1] 盛小平.基于知识网络的知识管理研究[J].图书情报工作，2004,(48):25-29.

[2] Bala V, Goyal S. A noncooperative model of network formation[J]. Economertica, 2000, 68(5):1 181-1 229.

[3] Jackson M O, Wolinsky A. A strategic model of social and economic networks[J]. Journal of Economic Theory, 1996,(71) : 44-74.

[4] 谢逢洁，崔文田，方一蔚．异构网络的有效性[J].系统工程，2008,26(6):93-97.

[5] Jackson M O, Alison Watts. On the formation of interaction networks in social coordination games[J]. Games and Economic Dehavior, 2002,(41):265-291.

[6] Giuseppe Confessore, Paolo Mancusoiuseppe. A dynamic model of R & D competition[J]. Research in Economics, 2002, 56(4):365-380.