基于A*算法的游戏地图寻路实现及性能比较

邱 磊

(武汉船舶职业技术学院电子系， 湖北 武汉 430050)

0 引 言

游戏，国外称之为“第九艺术”，是一种世界范围内的通用语言.随着互联网技术的应用以及软件技术的突破，人工智能的应用获得了进一步推广，而路径搜索是人工智能搜索技术的一个重要应用领域.目前中国网络游戏、手机3G增值等业务迅速发展，寻路技术已经成为众多游戏的一个核心组成部分.物体按照某种指定目的地的方式移动，其就要求程序必须能够找到一条从起点到目标点的最佳路径，这条路径应该是绕过障碍物并且到达目的地最短的路径，完成这个任务的最好的算法就是A*.A*算法作为一种灵活的、高性价比的寻路算法，一直被游戏行业所广泛采用[1]，很多游戏中的寻路算法都基于A*算法，如红色警戒、帝国时代等.本质上讲，A*算法反复检查它已经看到但是还没有搜索到的最有希望的位置，当一个位置被搜索到其恰好就是目标时，A*算法结束；否则，为进一步的搜索它将记录这个位置的所有相邻位置.本文对比分析了各种寻路算法的性能，并针对A*算法，采用了3种不同的启发式函数以分析其对A*算法执行结果的影响.

1 A*算法的描述

A*算法是把常规方法(如Dijkstra算法)和启发式方法(如最佳优先搜索算法)结合在一起的更为折中的算法，相对于最佳优先搜索算法来说要更加贴近于Dijkstra算法，尽管基于“无法保证最佳解”的启发式方法，A*却能保证找到一条最短路径，即找到最优解.

A*是一种典型的启发式搜索算法，如果一个估价函数可找出最短的路径，则称之为具有可采纳性.A*算法是可采纳的，它的估价函数表示为：f(n)=g(n)+h(n)[2]，这里，f(n)是节点的估价函数，表示从初始节点经过节点n到目标节点的最佳路径的代价；g(n)表示从初始节点到任意节点n的代价；启发式函数h(n)是从节点n到目标节点的最小代价评估值.选择一个好的启发式函数是重要的，不同的启发式函数会影响A*的搜索性能，一个具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件是[3]：(1)搜索树上存在着从初始节点到目标节点的最优路径；(2)问题域是有限的；(3)所有节点的子节点的搜索代价值>0；(4)h(n)<=h*(n)(h*(n)为节点n移动到目标的实际代价值).

对于一个搜索问题，显然条件(1)、(2)、(3)都是很容易满足的，而条件(4)：h(n)<=h*(n)是需要精心设计的.由于h*(n)无法知道，所以一个满足条件(4)的启发策略h(n)就难能可贵了，一个好的h(n)的评价是：h(n)在h*(n)的下界之下，并且尽量接近h*(n).启发式函数可以控制A*的行为：

(1) 若h(n)=0，则A*演变成Dijkstra算法；若h(n)比g(n)大很多，则A*演变成BFS算法.

(2) 若h(n)<=h*(n)，则A*保证能找到一条最短路径，h(n)越小，A*扩展的节点越多，运行的就越慢；若h(n)>h*(n) ，则A*不能保证找到一条最短路径，但运行的较快；若h(n)=h*(n)，则A*不扩展别的节点，只寻找最佳路径，运行的非常快.

2 A*算法在复杂情况下的应用

2.1 A*算法的优化——分层寻路

分层寻路是一种比较有效的优化A*算法的方法.其基本思想是把二维地图(或三维空间)按不同的复杂层次来划分[4]，如图1所示.图中有4个屋子，标号为1、2、3、4，屋子之间有门，如虚线所示.假设要从1号屋子里的起始点走到3号屋子里的目的地，首先可以把地图分为两层：第一层只包括屋子和屋子之间的关系(门)，不考虑屋子里的细节，这层最简单.第二层是屋子内部的细节，比如桌椅等，这层比较复杂，所采取的步骤为：

(1) 对各个屋子之间整体使用A*算法，找到屋子1到屋子3的路径为1-2-4-3；

(2) 在2号与4号屋子之间设定中间目的地“子目的地1”，对1号和2号屋子的内部细节使用A*算法找到从起始点到“子目的地1”之间的路径；

(3) 让游戏角色走到2号屋子的门外；

(4) 再确定中间目的地“子目的地2”，依次类推，对2号和4号屋子的内部细节使用A*算法.

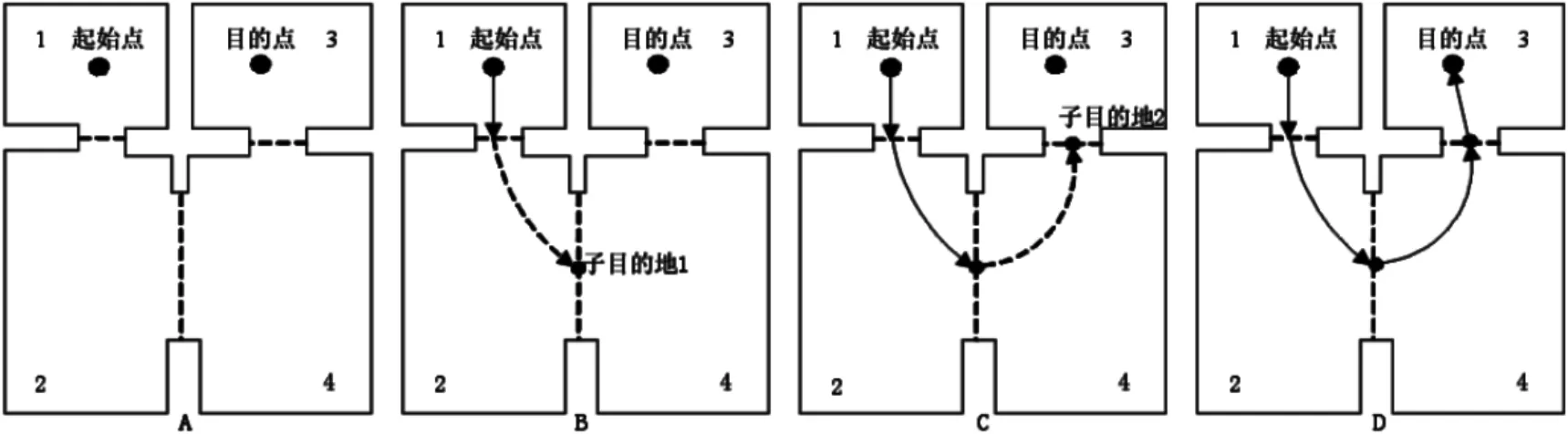
图1 分层寻路

2.2 游戏地图的划分

应用A*算法之前，应先对游戏地图进行划分，划分后的每个地图小块视为一个节点，图2(A)是基本地图，3个黑色区域为障碍物，底下的圆圈为起始点，最上面的圆圈为目的地.

栅格法是一种最简单的划分方式，也是本文所采用的方式，如图2(B)，首先把地图等距离地划分为大小相同的格子，然后根据黑色在一个格子中所占面积的百分比来决定这个格子的属性，比如说40%以上就认为这个格子是不可穿越的，如图2(B)中阴影的部分,这样就把具体的地图划分成可以使用A*算法搜索的地图了.

图2 划分地图的几种方法

四叉树法对栅格法作了改进，如图2(C)：不再把地图分成大小相同的格子，而是根据实际需要把地图分割成大小不同的格子.递归地将一个大的正方形格子划分为4个更小的正方形格子，直到每个正方形格子都有一致(或至少大部分一致)的地形.

适合于三维游戏的地图划分方法为导航网格法，如图2(D)，由于三维物体是由多边形构成的，游戏在处理时一般又把多边形再细分成三角形，三角形是游戏中三维空间的最基本的构成单元.导航网格的基本思想就是给每个三角形一个反映是否可以通过的属性，这样就可以对三维空间使用二维A*算法了.

可视点法采取了不同于上面几种方法的策略：它不再硬性划分地图的空间结构，而是在障碍物外的邻近地方取点，用几个点把障碍物包起来，如图2(E).用寻路算法时只需把这些点连接起来[4,5].

广义圆柱体法的基本思想是将相邻障碍物之间的空间看作一个2D圆柱体， 它的外形会在行进中进行改变.在每两个相邻的障碍物之间计算一个中心轴线，如图2(F)，这些线的交点为搜索提供了位置[6-8].

3 仿真实验对比分析

为了验证A*算法是一种比较高效的寻路算法，在26×20=520个节点的游戏地图上，首先利用栅格法按8方向连接对地图进行划分，然后分别采用A*算法(以曼哈顿距离为启发函数)、A*算法(以欧式距离为启发式函数)、A*算法(以切比雪夫距离为启发函数)、Dijkstra算法、双向广度优先搜索算法和动态A*算法5种算法进行寻路仿真实验，以对比分析各种搜索算法扩展节点的数量，图3～图7显示了5种算法的寻路演示结果.图8 给出了动态A*算法寻路的基本思想，由于只在非常小的区域中进行重新规划，充分利用了已经计算好的路径，因而使得整个寻路过程可动态适应游戏环境的变化.

图3 Dijkstra算法寻路演示 图4 双向广度优先搜索算法寻路演示 图5 A*算法(曼哈顿距离)寻路演示

接下来，在相同的26×20=520个节点的游戏地图上，采用与图3～图7相同的障碍物环境以及相同的初始节点和目标节点，对以上各种寻路算法的耗时进行分析.在路径求解过程中分别以0.007 813 s和0.003 906 s为每步执行计算的时间间隔，则各个算法的路径计算耗时如表1所示(误差范围小于0.01 s)：

由上述5种算法扩展节点的数量和计算耗时可知，虽然寻路的结果都可以保证找到最短路径，但各算法的性能明显不同.Dijkstra算法由于基于广度优先搜索策略，且没有启发式信息，因此遍历计算时扩展的节点数较多，从而效率低.双向广度优先搜索算法相对于广度优先算法来说，由于分别从初始节点和目标节点两个方向以广度优先的顺序同时扩展，搜索深度虽然得到了明显的降低，但扩展的节点数仍然较多，因此效率也不高.A*算法由于根据启发式函数的导向信息进行定向搜索，仅仅遍历了最短路径附近的相关节点，省去了大量无关节点的访问，计算量明显减少，因此极大地提高了路径搜索的效率，并且当绕过障碍物以后A*算法搜索的区域非常少.

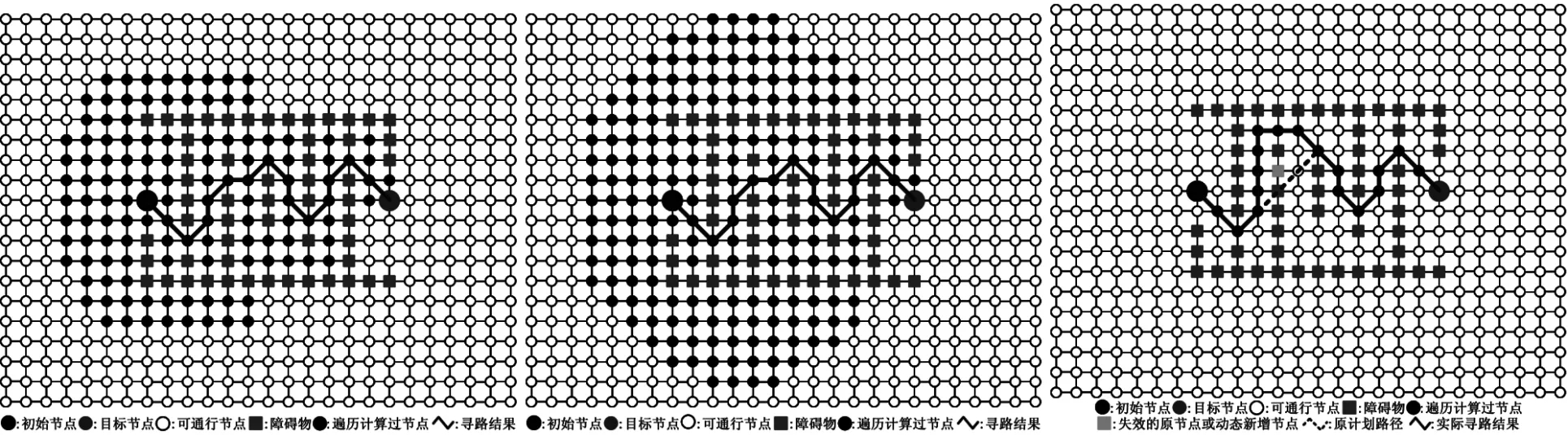
图6 A*算法(欧氏距离)寻路演示 图7 A*算法(切比雪夫距离)寻路演示 图8 动态A*算法寻路演示

表1 各个算法的路径计算耗时

启发式函数h(n)对A*算法的影响很大，以曼哈顿距离、欧式距离和以切比雪夫距离为启发函数，A*算法寻路时扩展节点的数量和计算耗时并不相同，可见所选的启发函数对A*算法很重要，一个好的启发函数有利于尽快找到最优解.另外，Dijkstra算法和双向广度优先搜索算法与A*算法求解的路径虽然都是最优路径，但并不完全一样，这是因为A*算法在搜索中加入了与问题有关的启发性的信息，以指导搜索朝着最有希望的方向前进.

因此，在游戏地图寻路效率上，A*算法的效率高于Dijkstra算法和双向广度优先搜索算法，A*算法的确是一种比较高效的寻路算法.

4 结束语

本文利用栅格法对游戏地图进行划分，对比了6种寻路算法的性能及启发式函数对A*算法性能的影响，但并未给出A*算法针对不同的游戏地图划分方式及执行效率差异的对比分析，下一步的研究将拓展到这个方面.另外，很多文献探讨了A*算法的改进优化问题，因此进一步提高算法效率的空间已非常狭窄[9]，公认的提高A*算法寻路性能以及寻路程序产生路径质量的一个方法是优化底层搜索空间，这将是一个有吸引力的课题.

参考文献

[1] 蔡方方，杨士颖. 双层A*算法在游戏寻路方面的研究[J]. 微型电脑应用, 2010, 26(1): 26.

[2] 马少平.人工智能[M]. 北京: 清华大学出版社, 2004: 32-34.

[3] EmilMatthew. Introduction to Heuristics Search—A*Algorithm Principle and Practice[DB/OL]. http://emilmatthew.51.net/EmilPapers/0632AStarSearch, 2006.

[4] Mark Deloura. A*速度优化. 游戏编程精粹1[M]. 北京:人民邮电出版社, 2004: 240.

[5] 叶 展, 叶 丁编. 游戏的设计与开发：梦开始的地方[M]. 北京: 人民交通出版社, 2003: 253-261.

[6] Kumar Pawan. Efficient Path Finding for 2D Games (Proceedings of CGAIDE’2004)[C]. Game Simulation and Artificial Intelligence Centre (GSAI), 2004: 265-266.

[7] 叶东曙. 基于碰撞的三维场景寻径算法研究[D]. 武汉:华中科技大学硕士学位论文, 2009.

[8] Yngvi Bjornsson. Fringe Search: Beating A*at Pathfinding on Game Maps[R]. School of Computer Science Reykjavik University Reykjavik, Iceland IS-103.

[9] 靳旭栋. 游戏领域中启发式寻径算法的运用和优化[D]. 上海:华东师范大学硕士学位论文, 2006.