基于单位分解的自适应跟踪控制设计

易 鸿

(四川文理学院物理与工程技术系， 四川 达州 635000)

0 引 言

目前对于线性系统的分析与设计已经形成了一套完整的理论体系，严格地说，一切实际系统都是非线性的，因此，现有的基于线性系统理论的研究结果和方法难以解决那些具体高度非线性的复杂系统分析和设计问题.微分几何方法是非线性系统的控制分析和设计的一个重要工具，单位分解是微分几何中的一个重要概念，它是与流形上的开覆盖紧密相关的，具有局部支撑及归一和的函数簇[1-3].在一个欧氏空间的紧致域上，单位分解的线性组合也具有以任意精度逼近连续函数的能力，利用这一性质可以去逼近非线性系统的不确定项或者控制器.

本文针对一类严格反馈非线性系统，在所构造控制器运行过程中波动不大的假定下，利用单位分解方法构造自适应控制器.以达芬强迫振动系统为仿真对象，仿真结果对本文给出的控制方法有效性进行了验证.

1 问题描述

考虑如下形式的非线性控制系统

x(n)(t)=f(x(t),…,xn-1(t))+bu(t)

(1)

y(t)=x(t)

其中，f为未知的非线性函数，u(t)∈Rn，和y(t)∈Rn分别为系统的输入和输出，b是控制增益.

(2)

那么将式(2)代入式(1)，得到闭环控制系统的方程：

e(n)(t)+k1e(n-1)(t)+…+kne(t)=0

(3)

由式(3)可知，因K的选取，可得t→∞时e(t)→0即系统的输出y渐进地收敛于理想输出ym.

2 基于单位分解的自适应跟踪控制设计

2.1 已知控制增益b

如果非线性函数f是已知的，则可以选择理想控制器来消除其非线性项，然后再根据线性控制理论设计控制器，如果f未知，理想控制器(3)很难实现.本文采用单位分解的方法逼近控制器，实现鲁棒自适应跟踪控制.

针对系统(1)，提出下列鲁棒控制器

u=ua+ub

(4)

其中

(5)

(6)

自适应率为：

(7)

将式(4)代入式(1)，可得如下控制系统的闭环动态方程：

e(n)(t)=-KTe(t)+b[u*(t)-ua-ub]

(8)

令

(9)

则动态方程(8)可表示为以下形式：

(10)

考虑如下Lyapunov方程

ATP+PA=-Q

(11)

对于给定的Q>0，方程(11)存在唯一正定矩阵解P.

(12)

一般情况下，随时间的变化u*(t)和ua(t)是光滑的，即u*(t)和ua(t)随时间的波动不大[4].所以即使ua(t)-u*(t)波动很大，ua(t-1)-ua(t)与u*(t-1)-u*(t)的波动还是保持较小.

考虑系统(1)，如果假设(1)式成立，则在非线性控制器(4)、(5)、(6)和自适应律(7)的共同作用下，闭环系统的输出跟踪误差渐进收敛到零点的一个小领域内.

2.2 未知控制增益b

其中

(13)

(14)

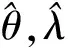
(15)

(16)

这里

(17)

r2,r3是实数，且与b同号.

考虑系统(8)，如果假设(8)成立，则在非线性控制器(13)、(14)和自适应律(15)、 (16)的共同作用下，闭环系统的输出跟踪误差渐进收敛到零点的一个小领域内.

3 仿真

考虑下面的达芬系统[5]：

(18)

图1 达芬系统

仿真1：当u(t)≡0，x1(0)=x2(0)≡2时，达芬系统(18)在相平面(x1,x2)上的轨.系统如图1所示，该系统出现混沌现象.

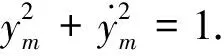
选取开覆盖为{UI}以产生式(6)中的单位分解{αi},i=1,2,3.

U1={x;‖x-a1‖<10,a1=(3,0)T}

(19)

U2={x;‖x-a2‖<10,a2=(-3,0)T}

(20)

U3=(-10,10)×(-10,10)

(21)

取状态初始值x1(0)=x2(0)=0，控制器的参数为：k1=2,k2=1，r=2,Q=diag(10,10),ε=0.

为了与模糊逻辑系统方法相比较，针对系统(18)，相应模糊逻辑系统的4个隶属函数为：

(22)

状态初始值保持不变，取xi(0)=x2(0)=2.

由仿真结果图2、3可以看出，基于单位分解的方法给出控制器产生的误差曲线比相同条件下由模糊逻辑系统构造的控制器产生的误差曲线具有更小的超调量，且收敛速度更快，另外，从基函数和覆盖域的选取上也可以看出，单位分解方法具有灵活性和简单性.这一点是模糊逻辑系统不具备的.

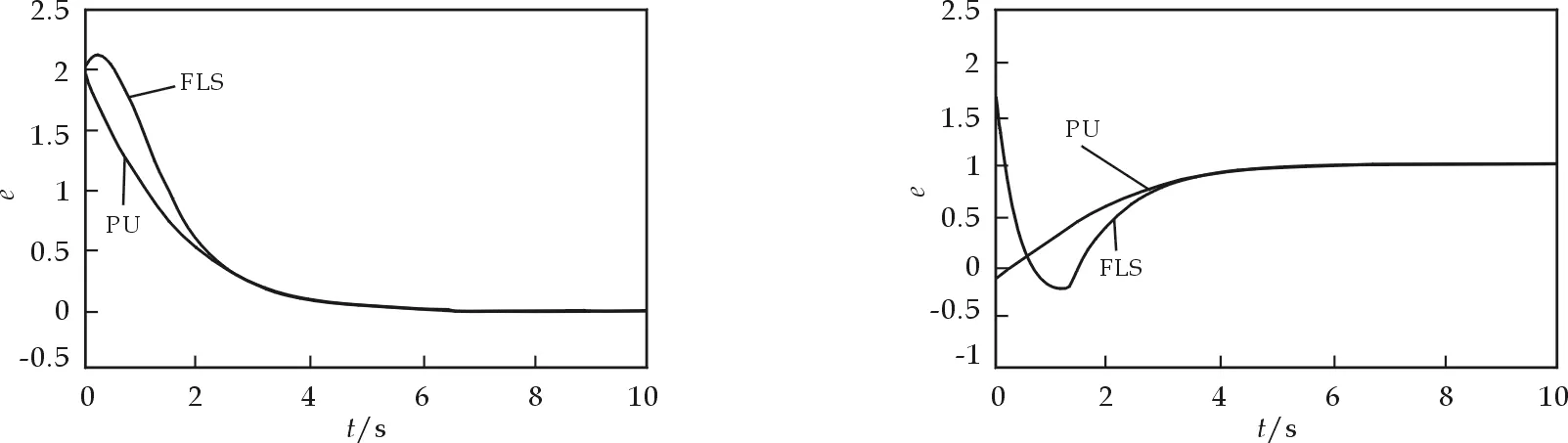
图2 系统状态的跟踪误差(增益b已知) 图3 系统状态的跟踪误差(增益b已知)

仿真3：这里假设控制增益b未知，但实际上b=1.利用单位分解方法，选取开覆盖为{UI}以产生式(7)中的单位分解{αi},i=1,2,3.

U1={x;‖x-a1‖<6,a1=(2,0)T}

(23)

U2={x;‖x-a2‖<6,a2=(2,0)T}

(24)

U2=(-6,6)×(-6,6)

(25)

取状态初始值x1(0)=x2(0)=2，控制器的参数为：k1=2,k2=1,r=2，Q=diag(10,10),ε=0.

同样为了与模糊逻辑系统方法相比较，针对系统(24)我们采用模糊逻辑系统方法[6-7]，相应模糊逻辑系统的4个隶属函数为:

(26)

取状态初始值x1(0)=x2(0)=2，作仿真如图4、5、6所示.

图4 系统状态的跟踪误差(增益b未知) 图5 局部放大的系统状态跟踪误差(增益b未知)

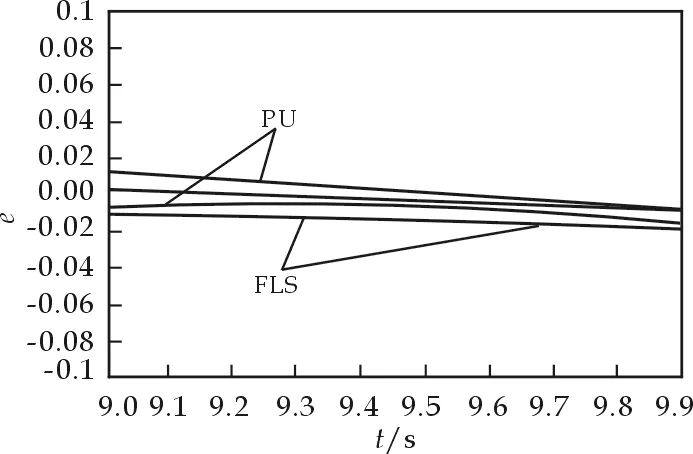
图6 局部放大的系统状态跟踪误差(增益b未知)

4 结束语

针对一类非线性系统，本文基于单位分解提出了一种设计自适应控制器的方法.由于单位分解自身具有的逼近非线性函数的能力以及其基函数选取的灵活性，使得这种方法可以看作是某些经典逼近方法，例如模糊控制,神经网络控制的一种补充，它直接对输入域进行几何剖分，并有效规避了模糊控制中维数灾难问题和神经网络控制的隐层数问题带来的弊端.另外，本文设计了自适应律在线调节单位分解的权系数，确保了我们选取的单位分解具有良好的逼近效果，不仅避免其选取不当造成系统不稳定的问题，而且拓展了单位分解法与自适应技术结合的控制设计研究.

参考文献

[1] B．Chen，X．P．Liu，K．F．Liu，etal．Direct adaptive fuzzy control of nonlinear strict feedback systems[J]．Automatica，2009，45(6)：1 530-1 535.

[2] 王银河，韩东方．基于单位分解的一类非线性系统变结构控制设计[J]．控制与决策，2006，21(8)：853-856.

[3] 王银河，张嗣赢．基于单位分解的一类非线性不确定系统跟踪控制设计[J]．控制理论与应用，2006，23(5)：699-702.

[4] P．L．QiN，X．Han，Y．Lin．Convergence alaysis about improved model-free adaptive controller based on multi-innovation theory[J]．ICIC Express Letters，2009，3(3A)：301-306.

[5] A．M．Zou，Z．G．Hou，M．Tian．Adaptive control of a class of nonlinear pure-feedback systems using fuzzy backstepping approach[J]．IEEE Transactions Fuzzy Systems，2008，16(4)：886-897.

[6] M．Wang，B．Chen，S．L．Dai．Direct adaptive fuzzy tracking control of a class of perturbed strict-feedback nonlinear systems[J]．Fuzzy Sets and Systems，2007，158(24)：2 655-2 670.

[7] M．Wang，B．Chen，X．P．Liu，etal．Adaptive fuzzy tracking control for a class of perturbed strict-feedback nonlinear time-delay systems[J]. Fuzzy Sets and Systems，2008，159(8)：949-967.