Hilbert空间中的算子框架恒等式
2011-02-10李春艳
李春艳
(重庆科技学院数理学院,重庆401331)
1946年,Gabor[1]在进行信号处理时,引入了信号关于基本信号的分解,这种方法很快成为了与时间-频率方法相伴的谱分析的范例。1952年,Duffin和Schaeffer[2]在研究非调和Fourier级数时进一步提炼了Gabor进行信号处理的思想,引入了Hilbert空间中框架的概念。1986年,Daubechies,Grossman和Mayer发现了框架理论在小波分析和Gabor变换中的应用[3],从而开创了框架理论的新时代。此后,框架理论被广泛的应用于信号处理,图象处理,数据压缩和采样理论等领域。
C.Y.Li和H.X.Cao在文献 [4]中引入了Hilbert空间中的算子框架的概念,说明了Hilbert空间中的框架,子空间框架等框架是算子框架的特例,并且对算子框架、算子Riesz基和算子框架的对偶框架等的性质进行了深入的讨论。下面,笔者将利用算子理论的方法,进一步讨论算子框架的的性质,并得到与算子框架相关的几个重要恒等式。
1 基本概念
用H表示Hilbert空间,用 Λ表示正整数集合,用l2(H)表示集合:

则称 T={Ti}i∈Λ为Hilbert空间 H中的算子框架,A,B称为框架界。若A=B,则称{Ti}i∈Λ为紧算子框架。若A=B=1,则称{Ti}i∈Λ为Parseval算子框架。不等式(1)如果只有右边成立,则称{Ti}i∈Λ为H 中的算子Bessel列,B称为{Ti}i∈Λ的界。
设 T={Ti}i∈Λ是H 中的算子Bessel列,定义算子:


定义1[4]设T={Ti}i∈Λ⊂B(H)是定义在Hilbert空间H上的一列算子,若满足以下条件:
(i)∀x ∈ H,有{Tix}i∈Λ ∈ l2(H);
(ii)存在正数A,B,使得:

如果T={Ti}i∈Λ是H 中的算子框架,令ST=RT*RT,则ST是一个可逆正算子。称ST为T={Ti}i∈Λ的框架算子。显然有:

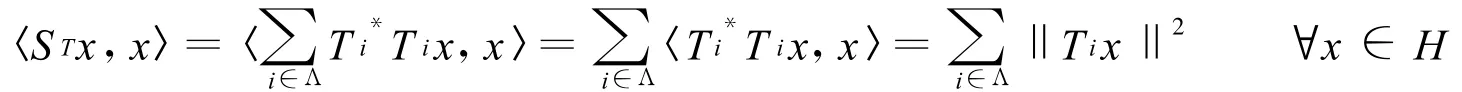
若J⊂Λ定义如下算子:

2 主要结果
设T={Ti}i∈Λ是H 中的一个算子框架,如果H中的另一算子序列 ~T={~Ti}i∈Λ满足如下条件:
则称 ~T={~Ti}i∈Λ为T={Ti}i∈Λ的对偶框架。在文献[4]中,已经知道 H 中的算子框架T={Ti}i∈Λ必定存在一个对偶框架 ~T=}i∈Λ。通常称 ~T={}i∈Λ为T={Ti}i∈Λ的经典对偶框架。下面给出关于算子框架的一些重要恒等式。
定理1 设T={Ti}i∈Λ是H 中的算子框架,ST是其框架算子,且 ~T={~Ti}i∈Λ是其经典对偶框架,则对任意的J⊂Λ,有:


因此:

对任意的x∈H,有:

类似地,对任意的x∈ H,由于 Λ-J∈ Λ,可得:
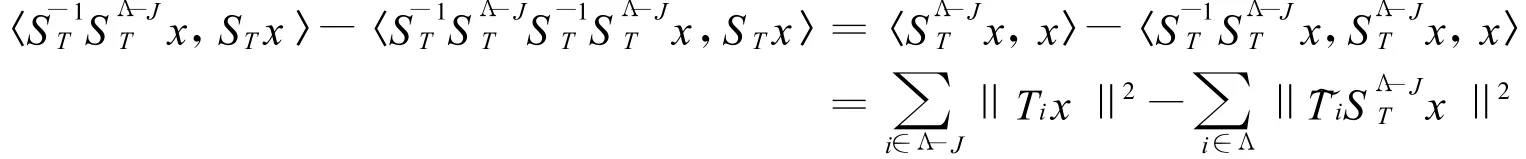
故:
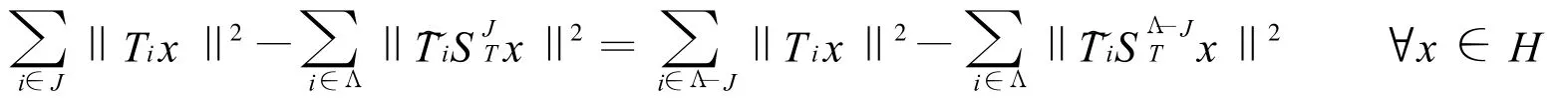
如果 T={Ti}i∈Λ是H 中的Parseval算子框架,则可以得到如下结论。
定理2 设 T={Ti}i∈Λ是H 中的Parseval算子框架,则对任意的J⊂Λ和 x∈ H,有:

证明 由 T={Ti}i∈Λ是H 中的Parseval算子框架可得:


所以ST-IH是自共轭有界线性算子,且ST-IH=0。故ST=IH。令~Ti=TiS-1T,显然,有~Ti=TiS-1T=Ti。对任意的J⊂Λ和x∈H,有:

由定理1可得:

即:

推论1 设 T={Ti}i∈Λ是H中的紧算子框架,其框架界为A,则对任意的J⊂Λ和x∈H,有:

证明 因为T={Ti}i∈Λ是H中的以A为界的紧算子框架,所以容易证明是 Parseval算子框架。由定理2即可得:

定理3 设 T={Ti}i∈Λ是H 中的Parseval算子框架,则对任意的J⊂Λ和 x∈ H,有:

所以:


[1]Gabor D.Theory of communications[J].J Inst Engrg,1946,93:429-457.
[2]Duffin R J,Schaeffer A C.A class of Nonhaarmonic Fou rier serier[J].T rans Amer Math Soc,1952,72:341-366.
[3]Daubechies I,Grossmann A,M eyer Y.Painless nonorthogonal ex pansion[J].J Math Phy s,1986,27:1271-1283.
[4]Li C Y,Cao H X.Operator Frames for B(H)[A].Wavelet Analysis and Applications[C].Sw itzerland:Birkh¨auser Verlag Basel,2006:67-82.
