多囚禁离子振动量子态Wigner函数的重构

宋明玉

(长江大学物理科学与技术学院,湖北荆州434023)

量子态的重构是量子光学及相关领域的核心问题。在原子-腔QED框架中,对于腔场量子态的测量人们已提出很多有效方案。同时,对于量子信息处理与量子计算的物理实现,囚禁离子系统正成为人们越来越关注的理想物理系统。最近人们提出很多方案,利用激光激发离子来实现囚禁离子振动非经典态,如Fock态[1],压缩相干态[2],猫态[3]和奇偶相干态[4]。在原子-腔QED系统中,腔场量子态的重构方案一般是通过对原子态测量来实现准概率分布函数,如Wigner函数的重构,从而提供一种新的量子态表象[5]。

最近,囚禁离子振动量子态的重构已在实验上得以实现,但该方案涉及复杂的数据分析。文献 [5]提出了在腔QED和离子阱中直接测量Wigner函数的方案,该方案适用于在低激发区域实现囚禁离子振动态的Wigner函数的直接测量。另一方面,在实际的实验中,离子阱不可能是完全孤立的,因此必须要考虑相应的耗散效应。

1 模 型

笔者研究在考虑系统耗散的情况下 (真实条件)振动态的重构问题。虽然不可能重构 Wigner函数,但仍然可能恢复初始态的全部信息。事实上,文献 [6]已经指出重构方案本身也显示量子系统的相干损失。与先前的方案不同的是,笔者的方案在色散时出现耗散的情况下仍然有效。

考虑N个质量为m的超冷离子囚禁在一个线型阱中,离子在阱中沿z方向排成一条链做集体振动,通过2束拉曼光调谐离子振动的第q阶上下边带。因为离子已经被冷却,每个离子仅仅在阱的轴线上相应平衡位置zj0(j=1,2,…,N)做小的振荡[7]。旋波近似下,哈密顿量描述为:

式中,{a,br}和{a+,b+r}分别是频率为ν的质心振动模以及频率为νr的其他振动模的湮灭和产生算符;和σ表示第j个离子的上升、下降以及反转算符;ω和λ是跃迁频率和特征离子内部跃迁的偶极矩阵zj0元;H.c.表示 E+(z,t)的厄米共轭;E+(z,t)是激光的正频部分:

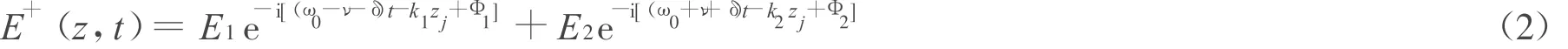
式中,El表示驱动激光场的幅度;Φl表示激光的相位;kl(l=1,2)表示波矢;δ表示驱动场对应离子跃迁频率的失谐量。在Lamb-Dicke极限下,笔者选择合适的激光相位、幅度参数以满足如下条件:

式中,Ψl=λEl对应激光的 Rabi频率。

假设与角动量J的x、y、z分量有关的算符如下:

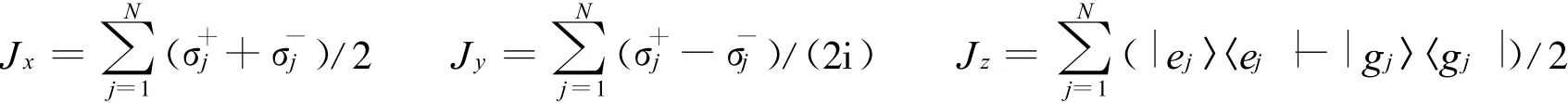
其中 ,|ψm(α)〉 =D(α)|ψm(0)〉,D(α)=exp(αa+-α*a)。

角动量的x分量J x能被写作:

从而:

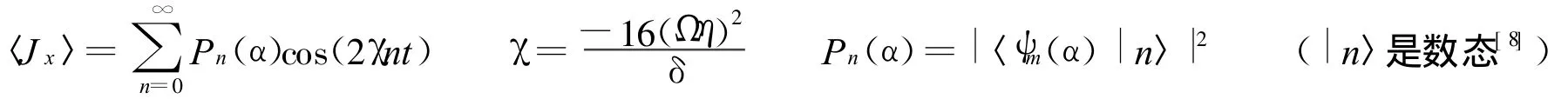
如果相互作用时间t满足t=π/(2χ),就得到:

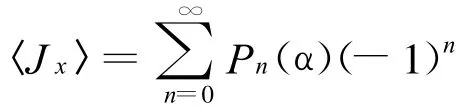
这正是Wigner函数 (有一个相因子π)[5,9]。

2 耗散条件下Wigner函数的重构

在色散近似及相互作用绘景下,特征离子动力学行为的主方程[10]为:

式中,ρ为系统的密度矩阵元。下面笔者将用超算符技术[11]来求解该方程。定义超算符:

其中 ,[K,L]ρ=(Γρ+ρΓ+)Kρ。对于初态 |ψm(α)〉,可以得到[12]:

为了获得系统的密度矩阵元,利用用上面定义的超算符来操作:

因为f是对离子内态的超算符,它只对离子的内态跃迁产生影响。而K是相应于离子的外部自由度的算符,它仅仅对离子的振动态产生影响。因此不难得到:

式中,C.C.表示复共轭。

因此:

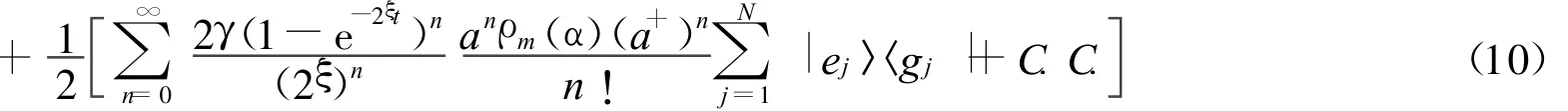
根据式(6)、(8)、(10)计算〈Jx〉得到:

对式(11)中第2个求和指数做修正M=m+k,得到:

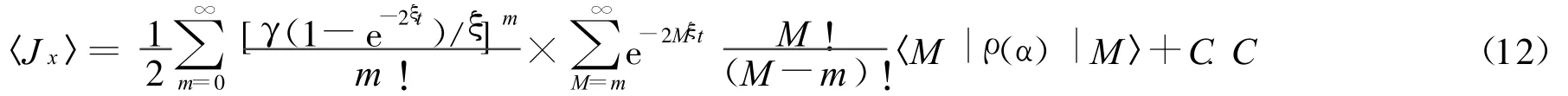
对式(12)的第2个求和符号从M=0开始,得到:

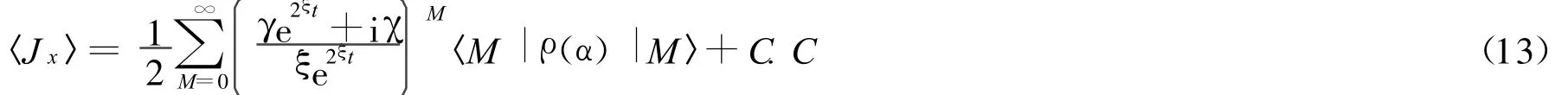
通过选择参数条件t=τ/χ和γ=Aχ,有:

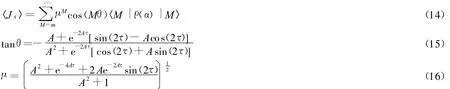
如果条件τ=3π/4和 A=exp(-3Aπ/2)能得到满足,则μ=0。此时,在方程(14)中仅仅保留的项是M=0的项。从而获得 Wigner函数:

通过数值方法很容易得到A=0.27。也就是说,仅仅用一个参数γ(在这里为γ=0.27χ)就能得到离子振动态全部信息。

3 实 例

如果离子的振动态处在2个幅度相等位相相反的相干态(|α〉和|-α〉)的迭加,其密度矩阵描述为:

式中,φ为相因子;N为归一化系数。

在耗散条件下,薛定谔猫态是极其脆弱的,因此这里以实现其Wigner函数的重构正好能来验证笔者的方法是可行的。

选择合适的相互作用时间来满足条件θ=-π,按照式(18)改写式(14):

在式(16)中,选择条件 A=0.1,μ是时间τ的函数(随τ的增大而减小)。在τ=0时,μ=1,很快随着τ的增加,使得 μ≠1。设置参数s,让 μ=(1+s)/(1-s),对应于τ=1.69,即 A=0.1,可以得到以s为参数的Wigner函数:

图1(a)数值模拟了满足条件α=3和φ=0初始时刻τ=0(s=0)的离子振动薛定谔猫态 (18)的Wigner函数分布,在图1(b)中,通过设置参数s=-0.18(对应于τ=1.69和A=0.1),数值模拟了同样态的分布。结果表明,重构准概率分布不再表现出负值,这反映了退相干过程。衰减参数越大,表现越明显。

4 结 语

提出了一种囚禁离子振动态的Wigner函数重构的一种预备方案,不同于以往方案的是,笔者的方案在耗散条件下的色散区仍然有效。该方案可以使用超级算子解决真实实验条件下 (包含耗散)的色散相互作用。结果证明,在非理想条件下,运用S-参数化的准概率分布函数可以实现甚至包括耗散情况下的振动量子态的全面重构。

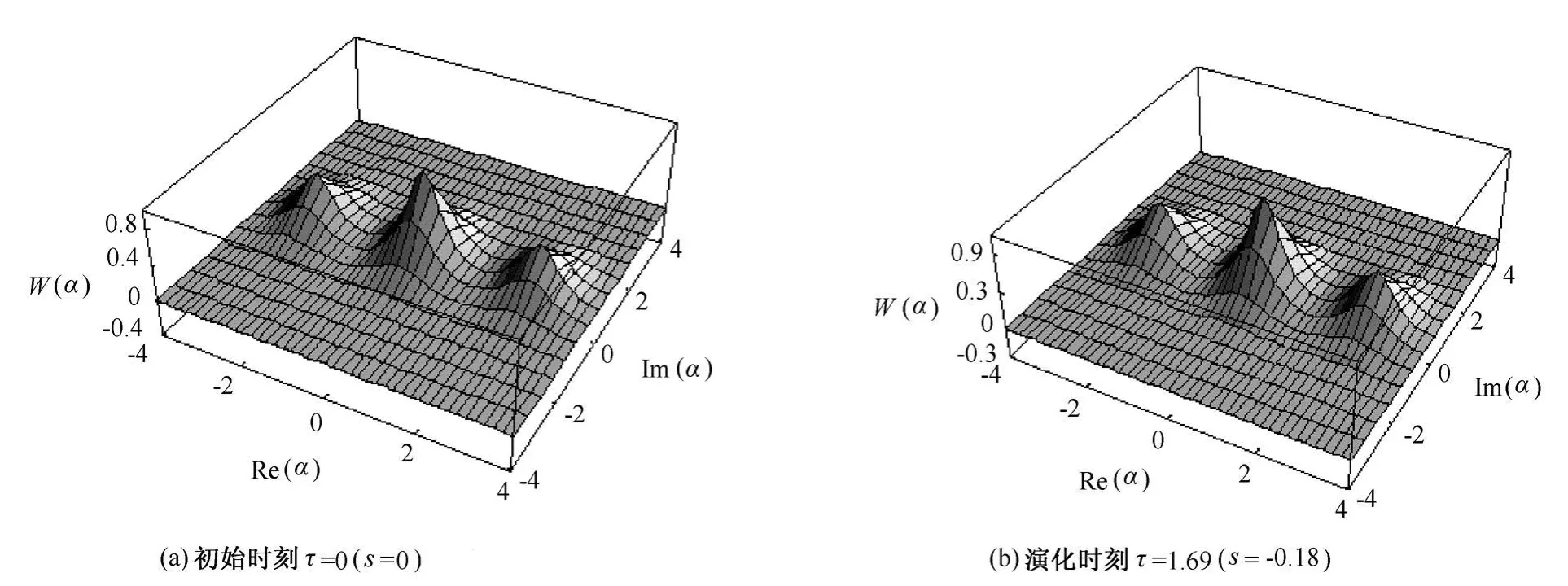
图1 满足条件α=3和φ=0的离子振动薛定谔猫态(18)的Wigner函数分布

[1]Cirac J I,Parkins A S,Zoller P.Preparation of Fock states by observation of quantum jumps in an ion trap[J].Phys Rev Lett,1993,(70):762-765.

[2]Cirac J I,Parkins A S,Blatt R,etc.Dark squeezed states of the motion of a trapped ion[J].Phys Rev Lett,1993,(70):556-559.

[3]Filho R L,Vogel W.Even and odd coherent states of the motion of a trap ped ion[J].Phys Rev Lett,1996,(76):608-611.

[4]Yang W X,Gong X L,Li J H.Efficient scheme for mesoscopic superpositions of motional coherent and squeezed coherent statesof N trapped ions[J].Phys Rev A,2004,(70):033812(1-6).

[5]Lutterbach L G,Davidovich L.Method for direct measurement of the wigner function in cavity QED and ion traps[J].Phys Rev Lett,1997,(78):2547-2550.

[6]Leonhardt U,Paul H.Realistic optical homodyne measurements and quasiprobability distributions[J].Phys Rev A,1993,(48):4598-4604.

[7]Solano E,Filho R L,Zagury N.Mesoscopic superpositions of vibronic collective states of N trapped ions[J].Phys Rev Lett,2001,(87):060402(1-4).

[8]Wu Y,Yang X X.Jaynes-Cummings Model for a trapped ion in any position of a standing wave[J].Phy s Rev Lett,1997,(78):3086-3088.

[9]Moya-Cessa H,Knight P L.Sercis representation of quantum field quasiprobabilities[J].Phys Rev A,1993,(48):2479-2481.

[10]Sorensen A,Molmer K.Entanglement and quantum computation with ions in thermal motion[J].Phys Rev A,2000,(62):022311(1-11).

[11]Barnett S M,Knight P L.Dissipation in a fundamental model of quantum op tical resonance[J].Phys Rev A,1986,(33):2444-2448.

[12]Phoenix S J D.Wave-packet evolution in the damped oscillator[J].Phys Rev A,1990,(41):5132-5138.