基于EMD理论的短期负荷预测

2011-02-08张宇俊储琳琳施伟国

电力需求侧管理 2011年1期

唐衍，顾洁，张宇俊，储琳琳，施伟国

（1.上海交通大学电气工程系，上海 200240；2.上海市电力公司市南供电公司，上海 200233）

电力系统短期负荷预测结果对电力系统的优化调度和可靠运行影响显著，准确的负荷预测有助于提高系统的安全性和稳定性，能够减少发电成本。随着电力市场的建立和发展，短期负荷预测工作正在发挥着越来越重要的作用［1］。

负荷预测的一个核心问题是预测的技术和方法，即预测的数学模型［2］。除了回归模型法、时间序列法、趋势外推预测法等传统的预测方法之外，利用人工神经网络、模糊理论、小波分析法的短期负荷预测方法也在不断的走向成熟。文献［3］提出了一种模糊集分类的人工神经网络预测方法，把每小时的负荷数据根据天气分类，把模糊化的数据输入人工神经网络中进行训练并预测；文献［4］提出了基于自回归动平均的模糊预测方法；文献［5］提出了灰色预测和单指数平滑法的组合预测法。

但是目前短期负荷预测的预测方法都是从总负荷入手进行分析建模，未能充分关注负荷变化的各个组成成分，因而无法有效分析负荷的局部特性，影响了预测效果。本文结合电力系统短期负荷变化的特点，建立EMD分解与ARMA时序分析预测相结合的模型对短期电力负荷进行预测，仿真结果证明了该模型的有效性，且预测精度能够较好地满足实际需求。

1 EMD算法理论

1.1 EMD算法的提出

1998年，美国国家宇航局的Huang N E等人在对瞬时频率的概念进行深入研究的基础上，提出了一种新的信号处理方法——希尔伯特黄转换（Hilbert-Huang transform，HHT），即基于EMD的时频分析方法。1999年，Huang又对该方法进行了一些改进［6］。该方法的本质是对信号进行平稳化处理，用EMD将信号中真实存在的不同尺度波动或趋势逐级分解出来，产生一系列具有不同特征尺度的数据序列。

1.2 EMD算法的基本思路及步骤

EMD分解的基本思想是：假如一个原始数据序列x（t）的极大值或极小值数目比上跨零点（或下跨零点）的数目多2个（或2个以上），则该数据序列就需要进行平稳化处理。

对于给定的信号x（t）∈R1，其EMD的过程如下所示：

（1）找到x（t）所有的局部极值点。

（2）对极大值点和极小值点，利用样条插值的方法分别建立信号的极大值包络函数和极小值包络函数，并分别记为emax（t）和emin（t）。

（3）计算上包络函数和下包络函数的均值函数

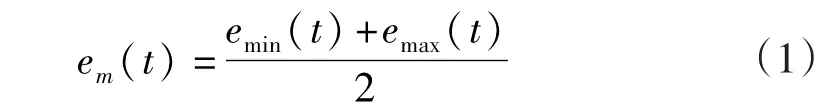
（4）计算信号x（t）与包络均值函数em（t）的差值函数

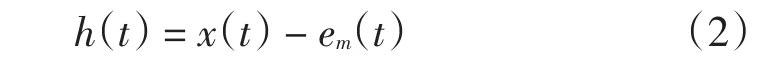
（5）用h（t）代替x（t），重复步骤（2）—步骤（4），直到所得到的包络均值趋于零，这样就得到了第一个IMF分量c1（t）。

由于c1（t）代表的是原始信号中的最高频成分，因此，可以得到原始信号x（t）中的低频信号

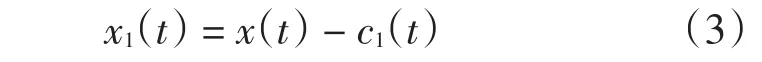
对x1（t）重复步骤（2）—步骤（4），就可以得到第二个IMF分量c2（t）。如此重复下去，直到得到的差值函数xn（t）是一个常值函数或者单调函数。最后，原始信号x（t）就可以由这些IMF函数cj（t），j=1，2，…，n，和趋势函数rn（t）来表示，如式（4）所示。

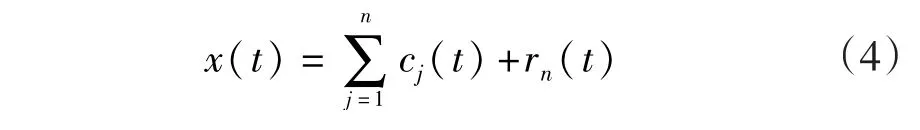
序列x（t）的EMD流程如图1所示。

图1 EMD流程

1.3 EMD算法的3个关键问题

（1）筛选过程停止准则

EMD分解过程实质上是一个筛选过程，但是在应用这一处理过程时必须注意：过多地重复该处理过程会导致本征模态分量变成纯粹的频率调制信号，而其幅度变为恒定的。为了保证本征模态分量保存足够的反映物理实际的幅度与频率调制信息，必须确定一个筛选过程停止的准则。这个筛选过程停止的条件准则可以通过限制标准差（standard deviation，SD）的值的大小来实现，SD的值通过计算2个连续筛选结果得到，如式（5）所示。

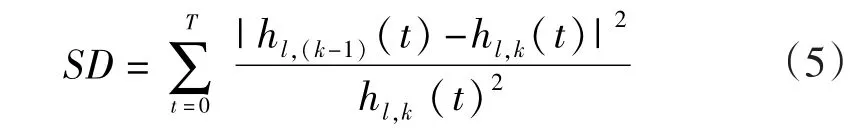
通常SD的值取在0.2～0.3之间时停止本次筛选，Huang提出的这个准则逐点比较了相邻筛选结果的差别。本文采用Huang提出的判断准则对筛选过程停止处进行判断。

（2）包络线拟合

曲线拟合是EMD中的关键问题，严格来说，这里讨论的拟合是指插值问题。插值方法对包络线拟合效果的好坏直接影响到EMD分解的结果，也将影响EMD方法的最终完善和推广。数值分析方法中有很多插值算法，如：埃尔米特插值法、阿克玛插值法、三次样条插值法等。后续的研究者又提出了不少改进，将高次样条插值法、多项式拟合法、分段幂函数插值法、B样条插值法等用于EMD分解算法中。

三次样条插值是一种既能克服高次多项式插值的缺陷又能保证一定光滑性的插值，在工程中应用广泛。但对于非均匀插值点，这种方法容易造成过冲和欠冲现象。另外，三次样条插值要运用矩阵解联立方程组，计算比较复杂［7］。综合考虑各拟合方法的优缺点，本文采用三次样条插值法作为包络线求取的办法。

（3）边界处理

边界处理问题主要是对信号两端数据进行一定的处理，以消除或减小边界效应［8］。一个较为基本的思想是对信号两端采用一定方法进行延拓，即在信号两端向外延伸处添加一定长度的数据点，使得有效数据区间的边界效应外移到延拓后的两端，从而减小边界效应对有效信号区间内的影响。目前常用的边界处理方法有：边界全波法、本征波匹配预测法、神经网络延拓法、多项式拟合法、镜像延拓法、包络延拓法和应用AR模型处理EMD边界问题的方法等。这些方法在一定程度上起到了抑制边界效应的作用。参考相关文献的研究成果并结合实际算例数据分析，本文采用多项式拟合算法进行处理。

2 基于EMD理论的短期负荷预测

2.1 电力负荷的构成

EMD理论可以把一个非平稳非线性的信号分解成多个分量的形式［9］，这些分量可以是不同频率的，而且叠加在一起就是原来的信号曲线。负荷曲线也可以分解出多个分量。通过对大量历史数据的分析可以发现：负荷主要包含典型负荷分量、天气敏感负荷分量、异常或特殊事件负荷分量以及随机负荷分量4个方面［10］，电力系统某一时刻的总负荷

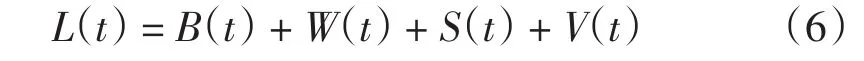
式中：L（t）、B（t）、W（t）、S（t）、V（t）分别为t时刻的系统总负荷、基本负荷分量、天气敏感负荷分量、特别事件负荷分量、随机负荷分量。

2.2 ARMA预测的步骤

ARMA预测方法的实现一般可以分为以下几个步骤：①根据时间序列的散点图、自相关函数和偏自相关函数图，以扩展单位根检验判断其方差、趋势及季节性变化规律，对序列的平稳性进行识别；②对非平稳序列进行平稳化处理；③根据时间序列模型的识别规则建立相应的模型；④进行参数估计，检验是否具有统计意义；⑤进行假设检验，诊断残差序列是否为白噪声；⑥利用已通过检验的模型进行预测分析。

2.3 基于EMD理论的短期负荷预测实现

对原始负荷序列进行EMD分解，利用ARMA预测模型对各分量分别进行预测后，将得到的各预测结果相加，从而得到最终的预测结果。在构建预测模型时还可以考虑气候因素的影响，并将其作为模型的一组输入，如图2所示。

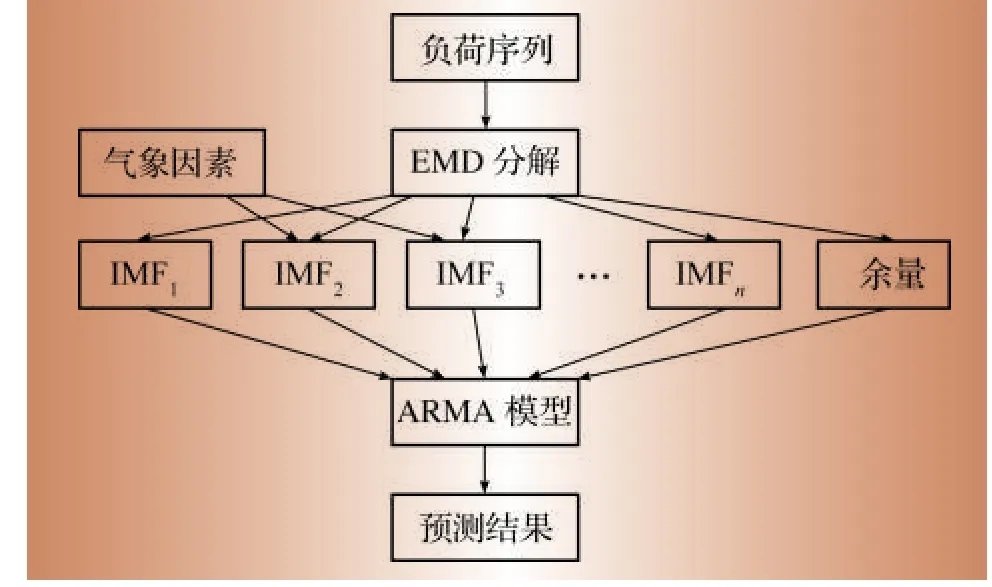
图2 基于EMD分解的短期负荷预测步骤

3 算例分析

3.1 算例简介

选取我国南方某地区2008年7月份连续5个星期工作日内的负荷值作为原始数据，应用本文建立的模型进行短期负荷预测。具体过程如下：从6月30日0：00开始，每隔1 h取一个负荷数据，至8月1日24：00为止，一共25天，共计600个负荷数据点。与此同时，取同一时间段的温度数据，以便找出负荷变动与温度变化之间的关系。该时段内的负荷曲线和温度曲线分别如图3、图4所示。

图3 工作日负荷曲线

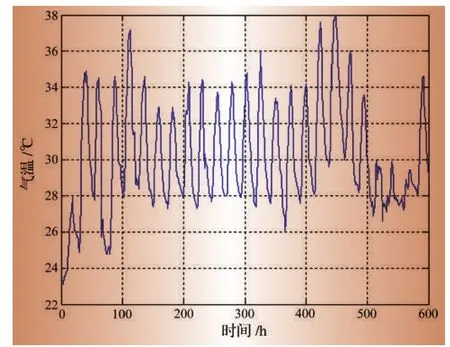
图4 工作日温度曲线

从图3可以看出，7月的大部分时间内负荷曲线周期性相对比较平稳，但在7月初和7月末时有较为明显的下偏趋势。观察对应时间的温度曲线可以发现：在负荷下偏的那段时间内，气温也相对偏低；在温度相对平稳的连续几天内，负荷曲线则处于平稳状态。

3.2 EMD分解结果分析

负荷序列的EMD分解结果如图5所示。图中：图a为原始负荷序列；图b—图g为负荷的各IMF分量；图h为余量。

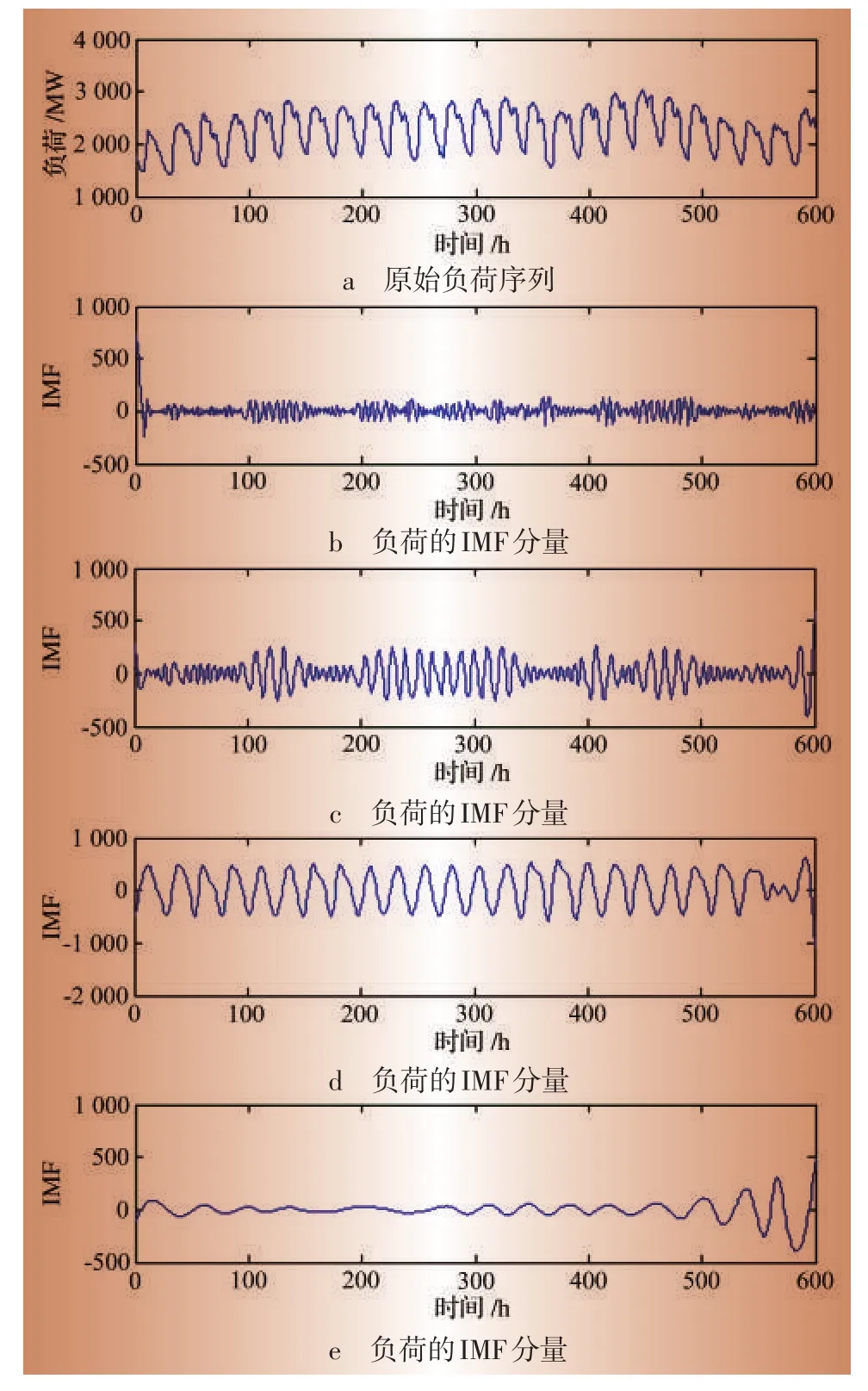
图5 负荷序列EMD分解结果

分析图5中每条曲线的规律，可以看出：图b中所示分量的幅值相对较小且频率很高，没有明显周期性，可判定它为负荷中的高频分量，即原负荷序列的随机分量；图c、图d中所示的分量具有较明显的周期性，幅值较大，故判定它们为原负荷序列的周期分量。其中：图c的幅值随时间的推移有一定的波动，可认为是气候敏感分量；图d的幅值在整个时间段内基本保持恒定，故为负荷的正常周期分量。图e、图f、图g所示的分量具有明显的趋势变化特征，随着时间的推移幅值逐渐变大，故将这几个分量划分为原负荷序列的趋势分量。剩余的图h所示的曲线则为趋势分量的余量。

由此，负荷序列被分解为了一系列具有规律性的、分别代表不同含义的分量，由于各分量变化规律不尽相同，因此对各分量分别进行预测，将能够有效地改善预测效果。

3.3 预测结果与分析

直接采用温度的IMF分量与负荷的IMF分量进行相关性分析并建立相关性模型进行预测的效果较差，所以进一步考虑各IMF的ARMA外推。预测过程为：在选取适当参数的情况下使用ARMA模型对分解出的负荷序列的每个IMF分量进行建模分析后，再根据拟合的模型进行沿拓预测，最后对预测结果进行分析。

3.3.1 ARMA参数选取

ARMA模型的阶数可以通过赤量信息准则（Akaike information criterion，AIC）来确定。AIC准则同时给出ARMA模型阶数和参数的最佳估计，适用于样本数据较少的问题。具体运用时，在规定范围内使模型阶数由低到高，分别计算AIC值，最后确定使其值最小的阶数，就是模型的合适阶数。

鉴于ARMA模型对历史样本的依赖性，以及考虑外推预测时间段内自变量的变化规律与历史数据的相关性，选取样本中前500 h的数据作为已知量，预测500～550 h之间的负荷变化，从而对模型进行验证。

3.3.2 预测结果与误差分析

对各IMF分量分别进行拟合预测之后，将它们的预测值以及趋势量的预测值相加就能得到最后的预测结果。将500～550 h时间段的负荷实际值与经过上述步骤得到的负荷预测值进行比较，如图6所示。直接用ARMA对原始负荷序列进行预测的同一时段的预测结果如图7所示。

对比图6与图7可以看出，经过EMD分解之后再进行预测的预测值，比未经过EMD分解而直接预测得到的预测值，更加接近真实值。经过EMD分解后预测得到的负荷值，在上下坡段几乎与实际值相重合，只在波峰和波谷处有略微的误差；未经EMD分解直接进行预测得到的负荷值，无论在峰谷或上下坡阶段，都存在着比较明显的误差。

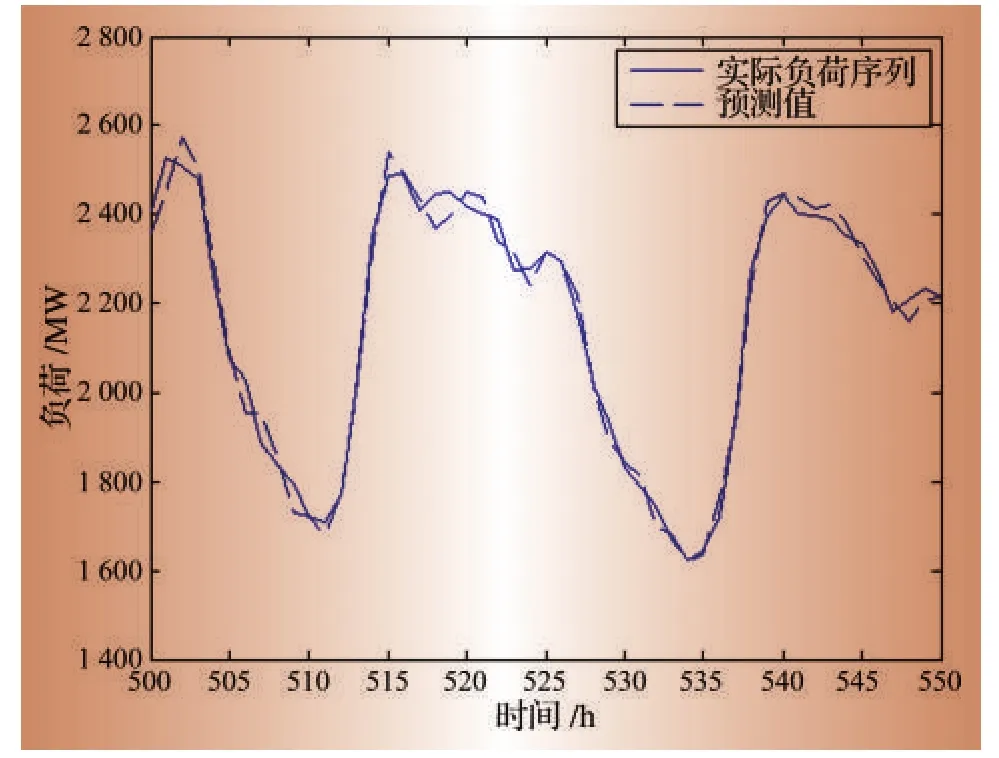
图6 各分量预测值相加所得值与实际值比较

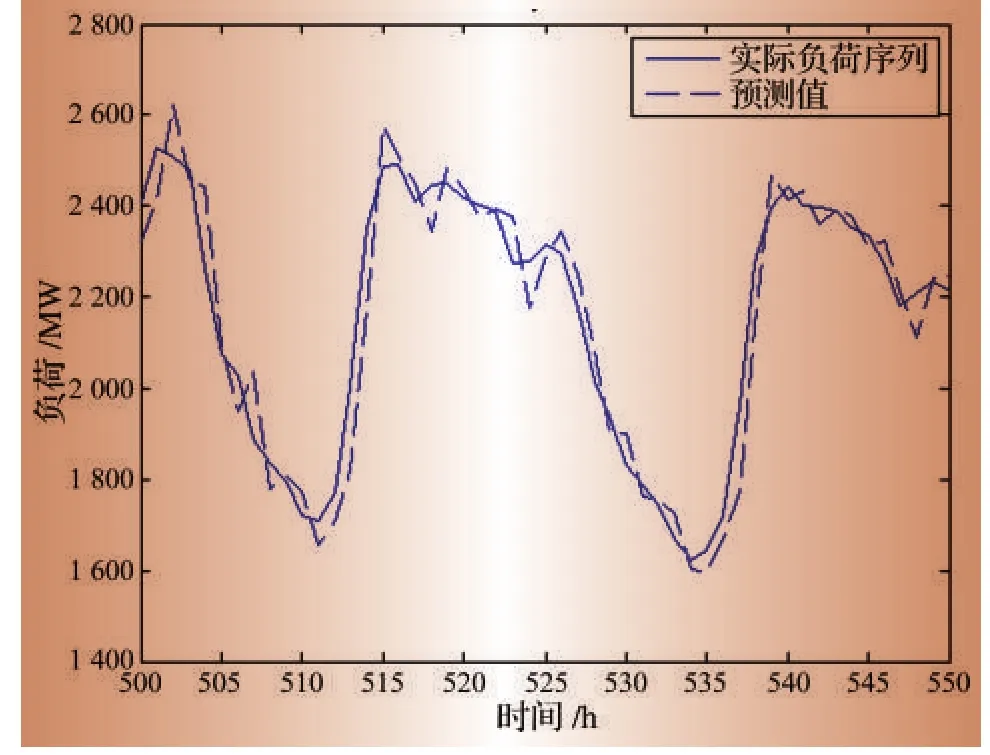
图7 负荷序列直接进行拟合预测结果与实际值比较

图8比较了该时段内2种预测途径得到的预测值与实际值的相对误差。从图中可以看出，EMD分解方法的相对误差比直接预测的相对误差小很多。

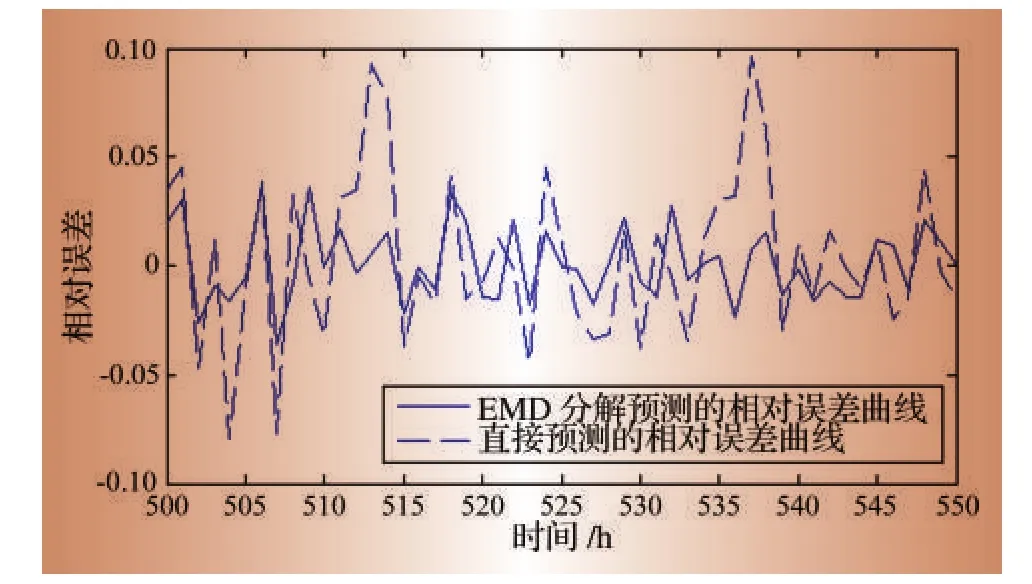
图8 2种预测方式相对误差比较

经计算，EMD方法预测结果的最大相对误差为3.71%，整体均方误差为1.71%，平均误差为1.41%；而不经过分解，直接运用ARMA进行预测所得的结果，最大误差高达9.63%，整体均方误差为3.76%，平均误差达3%。计算结果表明，运用了EMD分解法之后，负荷序列预测的精度有了大幅的提高，比直接利用ARMA时间序列法进行预测有明显的优势。