一种改进的基于FFT的PIV互相关算法

鲍晓利， 李木国

（大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

0 引 言

近年来，粒子图像测速（particle image velocimetry，PIV）技术得到了极大的发展，已被广泛应用于多个科研和工业领域.在2D－PIV技术中，基于相关窗口的互相关算法已被普遍采用［1］.随着对3D－PIV技术研究的不断深入，基于相关窗口的互相关算法也被应用其中［2、3］.在现有的实时PIV系统设计中，也多采用基于相关窗口的互相关算法［4］.同时，基本相关窗口的互相关算法也被用于相关领域，如三维运动检测［5］.当前对互相关算法的研究主要集中在提高算法精度方面，在提高算法运算效率方面的研究没有得到足够的重视，所以对互相关算法的运算效率进行研究，具有重要意义.到目前为止，在所提出的互相关算法中，基于快速傅里叶变换（FFT）的互相关算法由于其不受相关窗口大小限制，简化了互相关计算，并极大地提高了互相关运算效率，已成为互相关算法中最为典型的算法［6、7］.在粒子图像测速中，为提高粒子速度矢量分辨率，相邻相关窗口间须存在重叠，致使互相关运算中存在重复运算，降低了算法的运算效率［8］.本文在基于FFT的互相关算法的基础上，根据频域抽取原理，对互相关算法中的二维FFT进行改进，以减少互相关算法中的重复FFT运算.

1 粒子图像测速原理

PIV技术是在流动显示的基础上结合光学图像处理技术对待测量的流场进行非接触的高精度测量［9］.测速系统对加入示踪粒子的流场进行快速拍照，通过测量流场中示踪粒子在已知时间间隔内的位移实现对流体运动速度的测量.定义x（t）、y（t）为某个粒子在t时刻的位置，经过时间Δt粒子的位置为x（t＋Δt）、y（t＋Δt），那么该粒子在x轴、y轴方向的速度分量v x、v y如下式：

实际应用中，粒子在t＋Δt时刻的位置是未知的.对于粒子在t＋Δt时刻的位置，通常采用基于相关窗口的互相关方法来确定.

2 基于FFT的互相关算法

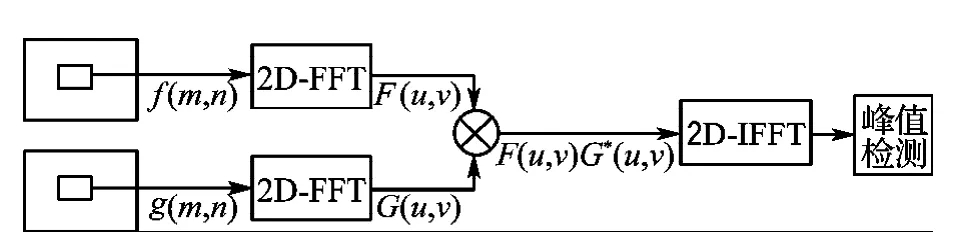
图1 基于FFT的互相关算法流程图Fig.1 FFT－based cross－correlation algorithm diagram

针对互相关算法运算量巨大的问题提出了较多算法，基于FFT的互相关算法由于具有极高的运算效率，至今仍为PIV互相关算法中的基本算法［10］.图1为基于FFT的互相关算法流程图.其中f（m，n）和g（m，n）分别表示当前窗口和询问窗口.t时刻粒子存在于（x，y）位置处窗口（即当前窗口），t＋Δt时刻粒子所在窗口未知.t＋Δt时刻粒子所在窗口位置（x＋ξ，y＋η）可利用当前窗口与t＋Δt时刻的粒子存在目标区域进行互相关运算获得.最大互相关峰值位置处窗口，即t＋Δt时刻粒子所在窗口.当前窗口与询问窗口的互相关函数如式（2）［11］.其中，当前窗口大小为M0×N0，

I1和I2分别表示在t时刻和t＋Δt时刻粒子图像的像素灰度值.

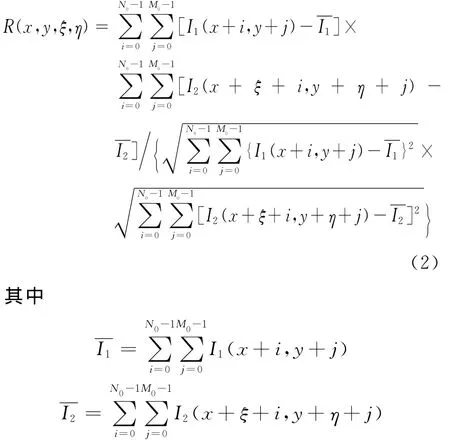
在基于FFT的互相关算法中，乘法运算量在互相关运算量中占绝对比重，所以对互相关运算量分析可简化为对其乘法运算量分析，具有等效的分析结果［11］.基于FFT的互相关算法的运算量计算表达式为

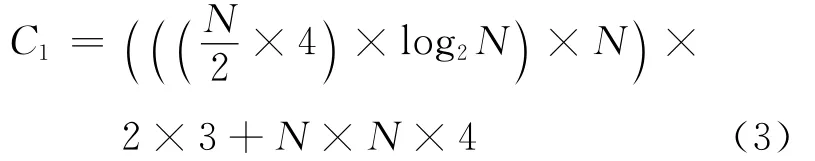
其中N×N为询问窗口大小，N满足2k（k为正整数），否则询问窗口须补零.

3 基于FFT的互相关算法的改进

一般情况下，相关窗口的重叠率为50%时，粒子速度矢量分辨率与算法运算效率之间达到最佳均衡［8］.频域抽取（DIF）基二维FFT算法中，信号的FFT由被分成上、下两部分的信号的FFT构成.据此原理，在窗口重叠率为50%时，对当前窗口和询问窗口进行对半分割，重叠相邻3个窗口的二维FFT中重叠部分窗口的一个维度的FFT运算值，可由其相邻窗口的重叠部分的FFT运算值经频移叠加后获得.据此，对基于FFT的互相关算法进行改进，以提高互相关算法运算效率.在询问窗口大小为M×N（M、N为2的整数次幂，一般情况下M等于N）时，重叠窗口的FFT表达式F2（u，v）推导过程如式（4）～（6）［12］所示：

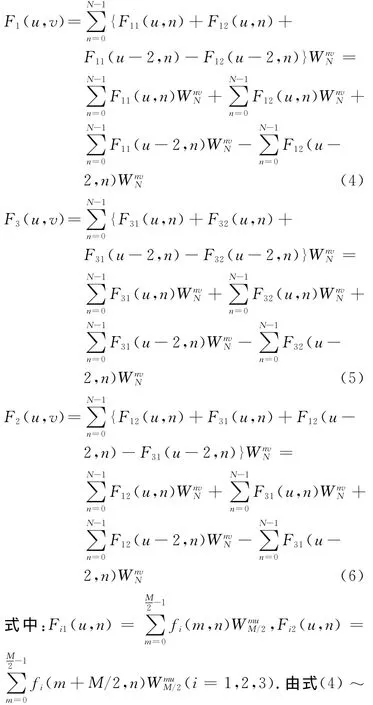
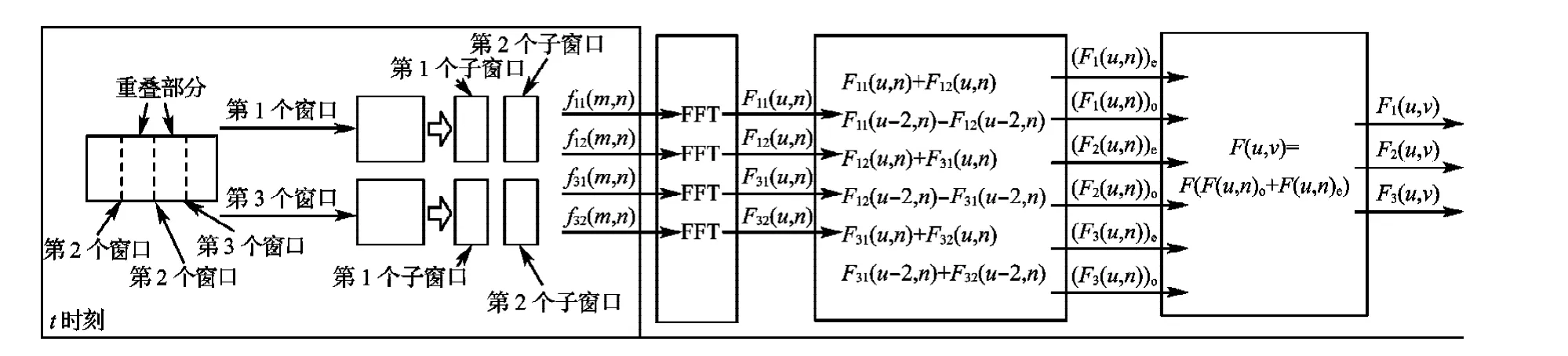
图2 改进的二维FFT计算流程Fig.2 Computational diagram of improved 2D－FFT

改进后互相关算法运算量仍采用乘法运算量来度量，其计算表达式如下式：

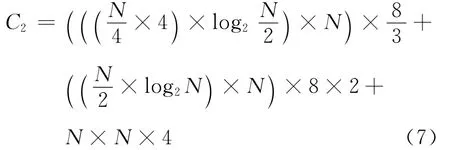
式（7）与式（3）相比较，改进后算法运算效率提高表达式如式（8）所示.改进后算法较未改进算法运算效率提高如图3（图中横坐标L表示询问窗口宽度，纵坐标σ表示算法运算效率提高）.

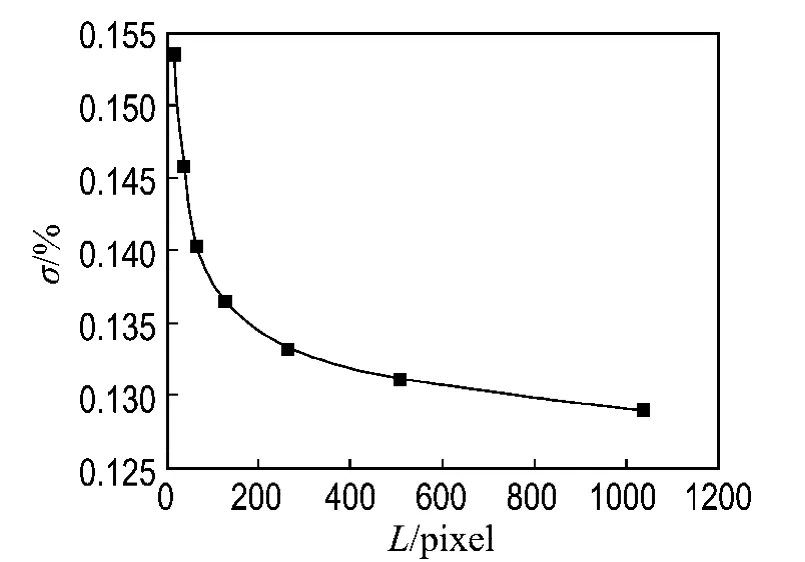
图3 改进后算法运算效率提高Fig.3 Computation efficiency increase of improved algorithm

从图3中可以看出，当询问窗口大小为16× 16、32×32、64×64、128×128、256×256、512× 512、1 024×1 024时，改进后算法较未改进算法在运算效率方面平均提高了13.86%，并随着询问窗口变大算法运算效率提高会减小.当询问窗口大小为16×16时运算效率提高最大，为15.38%.当询问窗口大小为256×256、512× 512、1 024×1 024时，其运算效率提高变化不明显.

4 实验结果与讨论

为对改进前与改进后算法进行对比验证及分析，利用CCD相机连续采集了30帧粒子图像，连续两帧粒子图像时间间隔为0.043 s，图像大小为1 600×1 200.随机选取连续两帧经预处理后的粒子图像（为清晰显示出图像中粒子，仅给出部分放大图像），如图4所示.

当询问窗口大小为16×16或1 024×1 024时，由于询问窗口所包含粒子信息过少或分析点数过少，粒子图像测速处理结果无任何实际意义.对于这两种情况本文均不做分析.

设置窗口重叠率为50%，在询问窗口大小分别为32×32、64×64、128×128、256×256、512× 512时，采用基于改进前后两种互相关算法的PIV算法计算粒子速度矢量.处理程序采用Matlab作为开发平台编写完成.限于篇幅仅给出当询问窗口大小为128×128时随机选取的粒子速度矢量对比图，如图5所示（图中横坐标和纵坐标的单位为像素）.

图4 连续两帧粒子图像Fig.4 A pair of particle images

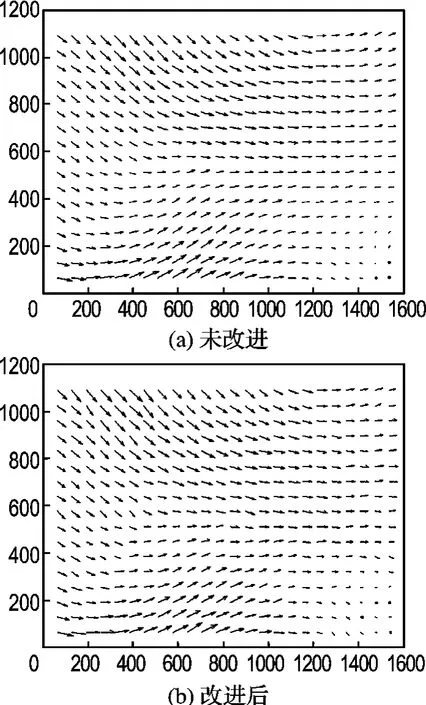
图5 粒子速度矢量对比图Fig.5 Comparison of two particle velocity vector′s images

对比观察图5（a）和（b）两粒子速度矢量图，发现其无任何差异.为定量分析改进前后两算法在所得速度矢量上的差异，对不同询问窗口大小下得到的粒子速度矢量在x轴和y轴方向上的平均差异进行对比分析，分析结果如表1所示.

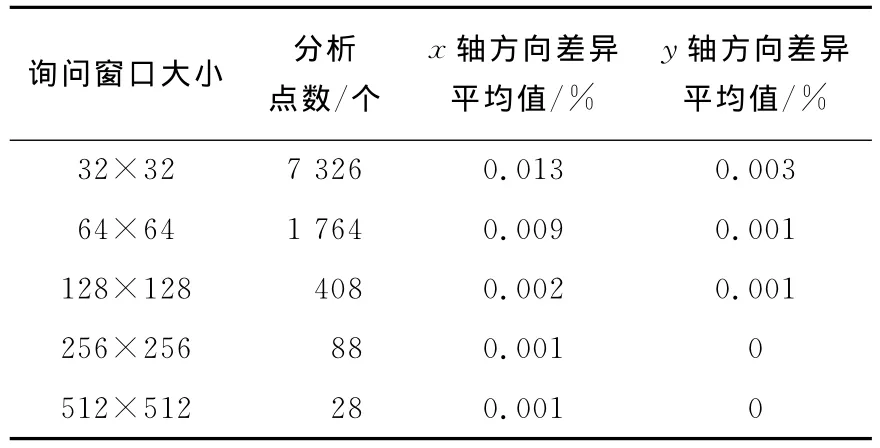
表1 粒子速度矢量对比Tab.1 Comparison results of particle velocity vectors

由表1可以得出，利用改进前后两互相关算法计算所得速度矢量在x轴和y轴方向上仅存在微小差异.

改进前后两种互相关算法平均消耗时间对比如表2所示.

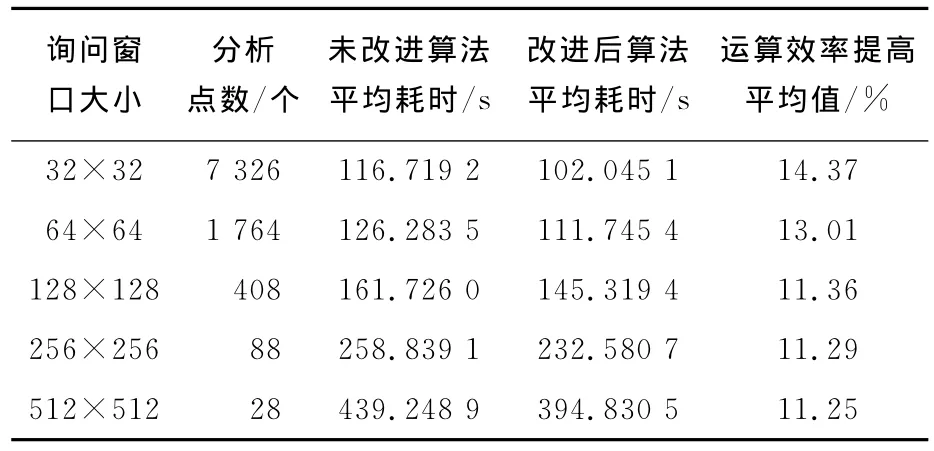
表2 算法消耗时间对比Tab.2 Comparison results of the processing time

由表2可以得出，改进后算法较未改进算法在运算效率方面平均提高了12.25%，与理论提高效率平均值十分接近.当询问窗口大小为32× 32时改进算法效率提高最高，为14.37%.当询问窗口大小为128×128、256×256、512×512时，随着询问窗口变大运算效率提高变化不明显.

5 结 论

本文利用频域抽取原理，在基于FFT的互相关算法的基础上，结合重叠窗口互相关运算的特点，对基于FFT的互相关算法进行了改进，有效地减少了互相关运算中重复FFT运算量.实验结果表明，本文所提出的改进互相关算法与基于FFT的互相关算法相比，在不降低PIV处理效果的前提下，运算效率平均提高了约12.25%.

［1］ADIRAN R J.Twenty years of particle image velocimetry［J］.Experiments in Fluids，2005，39（2）：159－169

［2］ZHANG Wei，HAIN R，KHLER C J.Scanning PIV investigation of the laminar separation bubble on a SD7003 airfoil［J］.Experiments in Fluids，2008，45（4）：725－743

［3］WIENEKE B.Volume self－calibration for 3D particle image velocimetry［J］.Experiments in Fluids，2008，45（4）：549－556

［4］MUNOZ J M I，DELLAVALE D，SONNAILLON M O，etal.Real－time particle image velocimetry based on FPGA technology［C］／／5thSouthern Conference on Programmable Logic.Brazil：IEEE，2009

［5］ALVAREZ L，CASTANO C A，CARCIA M，etal.3D motion estimation using a combination of correlation and variational methods for PIV［J］.Computer Aided Systems Theory，2007（4739）：612－620

［6］ADRIC E，VLACHOS P P.Assessment of advanced windowing techniques for digital particle image velocimetry［J］.Measurement Science and Technology，2009，20（7）：1－9

［7］王灿星，林建忠，山本富士夫.二维PIV图像处理算法［J］.水动力学研究与进展，2001，16（4）：399－404

［8］ROTH G I，KATZ J.Five techniques for increasing the speed and accuracy of PIV interrogation［J］.Measurement Science and Technology，2001，12（3）：238－245

［9］高殿荣，王益群，申功炘.DPIV技术及其在流场测量中的应用［J］.液压气动与密封，2001，21（5）：30－33

［10］STANISLAS M，OKAMOTO K，KHLER C J.Main results of the second international PIV challenge［J］.Experiments in Fluids，2005，39（2）：170－191

［11］TOSHIHITO F，KENJI F，TSUTOMU M.A realtime visualization system for PIV［J］.Field－Programmable Logic and Applications，2003，2778（1）：437－447

［12］胡广书.数字信号处理（理论、算法与实现）［M］.2版.北京：清华大学出版社，2003：176－177