修形斜齿轮啮合性质及误差影响分析

尚振国， 王德伦

（大连理工大学机械工程学院，辽宁大连 116024）

0 引 言

随着风力发电增速器、船舶推进器等大功率齿轮传动装置向高速化、大型化、重载化和环保化方向发展，齿轮传动装置的振动和噪声问题日益突出，齿轮修形技术成为解决齿轮传动装置的振动和噪声的有效途径.文献［1］总结了直齿轮齿廓修形理论.Litvin等应用轮齿接触分析技术研究了齿廓和齿向采用二次曲线的双鼓形修形斜齿轮的啮合区域及传动误差［2～4］.方宗德、常山等应用柔度系数法，并以荷载均布和传递误差最小为目标函数，以数学规划法确定齿轮修形参数［5～8］.Wagaj等采用有限元接触分析技术，以修形量、修形长度、齿向修鼓量等为参数，计算了不同参数下2D修形和3D修形齿轮弯曲应力和接触应力的变化情况［9］.

本文在考虑制造、安装误差等实际啮合条件下，分析一种保留部分渐开线齿面的局部修形斜齿轮的啮合轨迹及安装误差对啮合轨迹的影响.

1 含误差的齿面啮合方程

1.1 坐标系

图1 实际齿面坐标系Fig.1 Coordinate systems of real tooth surface

如图1所示，用3个坐标系表示被动齿轮实际齿面.坐标系S6（O6－x6y6z6）与理论齿面固连，坐标系S4（O4－x4y4z4）与实际齿面固连，坐标系S2（O2－x2y2z2）为随被动齿轮一起转动的动坐标系，引入固定坐标系Sf（Of－xfyfzf）与机架固连.S6→S4的坐标变换矩阵M46代表实际齿面与理论齿面之间的误差，包括齿形误差、受载变形及几何修形，用沿接触点公法线距离δ2表示，对应的齿轮转角误差用Δψ2表示；S4→S2的坐标变换矩阵M24代表实际齿轮轴线与理论齿轮轴线之间的平行度误差及位置误差（中心距误差）；S2→Sf的坐标变换矩阵Mf2代表在固定坐标系Sf中的曲面族.

同样引入坐标系S1、S3、S5表示主动齿轮实际齿面.

在初始位置，S1与Sf重合，x2与xf同向，y2与yf重合，z2与zf同向，坐标原点O2、Of间的距离等于齿轮副中心距.

1.2 齿面啮合方程

齿面Σ1和Σ2在固定坐标系Sf中的曲面族方程为

同样地，可以得到齿面Σ1的坐标变换矩阵Mf1、M13、M35，这里不再赘述.

齿面Σ1和Σ2在固定坐标系Sf中的单位法向量为

L为各坐标系间的坐标变换矩阵，由对应M矩阵去掉最后1行和最后1列得到.

齿面Σ1和Σ2在固定坐标系Sf中任意瞬时连续相切接触的条件为

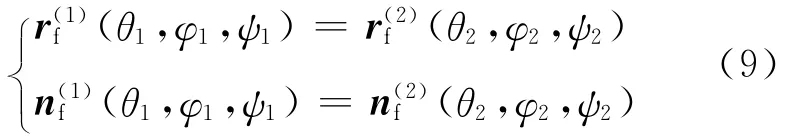
方程组（9）称为含误差的齿面啮合方程［10］.

方程组（9）、（10）包括两个矢量方程，共有6个未知数（θ1，φ1，ψ1，θ2，φ2，ψ2），但只能生成5个标量方程，因为‖‖＝‖‖.如果给定主动齿轮转角ψ1，就可以求出其他5个参数θ1（ψ1）、φ1（ψ1）、θ2（ψ1）、φ2（ψ1）、ψ2（ψ1）.

1.3 接触迹线和传递误差

接触迹线：如图2所示，主、被动齿轮接触点的轨迹，称为接触迹线（contact path），用符号Pc表示.

接触迹线在齿面Σ1上表示如下：

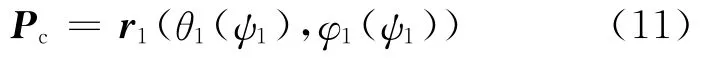
传递误差：如图3所示，被动齿轮实际啮合位置与理论啮合位置之差，称为传递误差（transmission error），用符号Et表示.

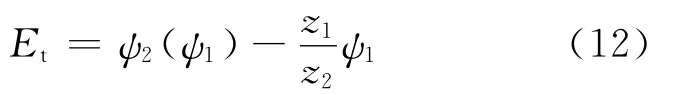
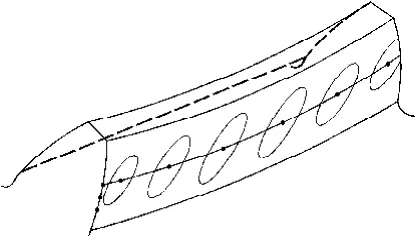
图2 接触迹线示意图Fig.2 Schematic plan of contact path

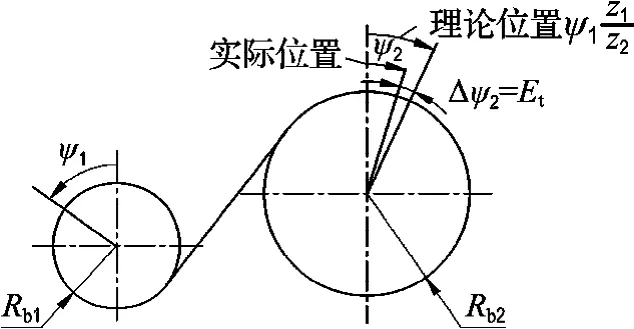
图3 传递误差示意图Fig.3 Schematic plan of transmission error

2 齿面方程

令直角坐标系S1（O1－x1y1z1）的坐标原点取在轮齿中间截面与齿轮轴线的交点上，y1轴通过节点p，z1轴沿齿轮轴线方向，如图4所示.齿面Σ1的参数方程可以表示成

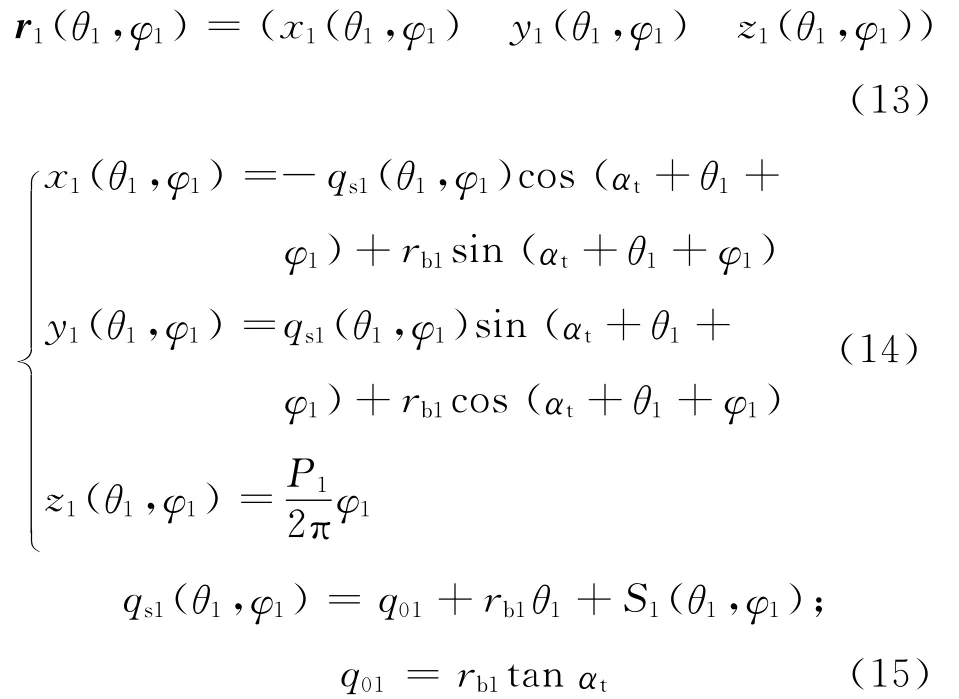
图4 主动齿轮坐标系Fig.4 Coordinate system of driving gear

同样地，在直角坐标系S2（O2－x2y2z2）中齿面Σ2的参数方程可以表示成

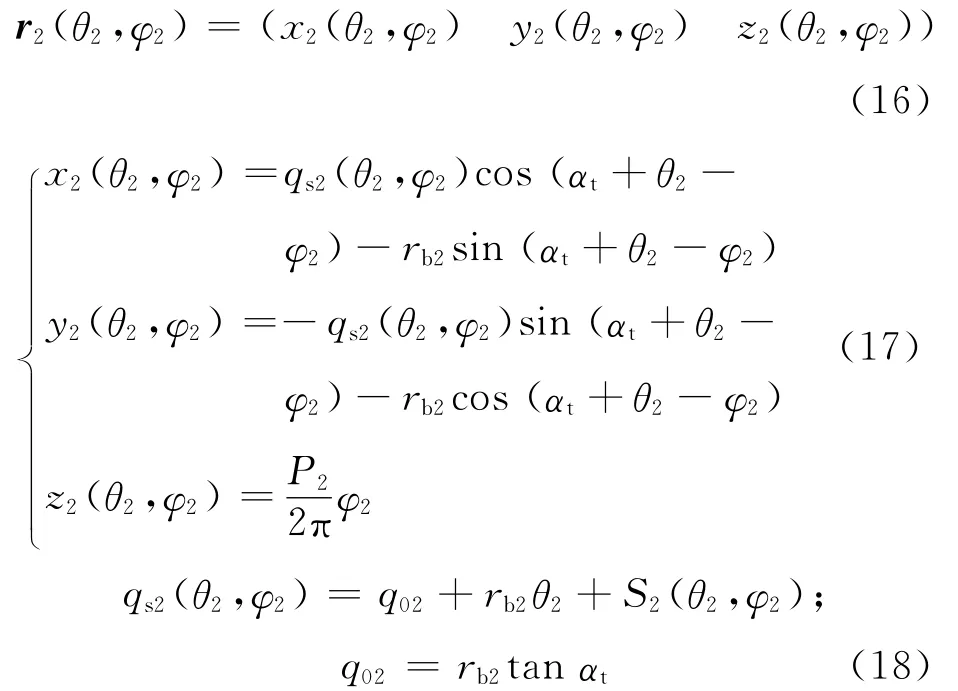
其中S2（θ2，φ2）为齿面Σ2的修形曲线方程.

3 修形曲线方程

齿轮修形包括齿廓修形和齿向修形.齿廓修形是指沿齿高方向从齿面上去除一部分材料，从而改变齿廓形状.齿廓修形的参数包括修形量、修形长度和修形曲线.

修形量是指齿廓上任意位置沿法向去除材料的厚度.齿顶和齿根部位修形量最大，如图5中et1、er1所示（下标t表示齿顶，下标r表示齿根，下同）.

修形曲线表示齿廓上任意位置与对应修形量的关系，如图5中γ1所示.

修形长度是指修形曲线在齿廓上的起始点至齿顶或齿根终止点的距离，可以在齿轮副啮合线上用起始点对应的发生线滚动角表示，如图5中θt1、θr1所示.

齿向修形包括螺旋角修形和齿端修鼓两种形式.齿向修形参数包括螺旋角修形量Δβ（在齿面方程中直接以螺旋角大小表示），齿向修形量h11、h12，齿向修形长度b11、b12，齿向修形曲线ζ1，如图5所示.

在这里，主动齿轮的齿顶和齿根采用二次抛物线修形［12］，修形起始点取单双齿啮合转换点θt1、θr1.齿的两端也采用二次抛物线修形，修形长度b11和b12用对应的端面截形旋转角φmin1、φ11、φ12、φmax1表示，如图5所示.这样，修形曲线方程可以表示成

图5 主动齿轮修形示意图Fig.5 Schematic plan of driving gear modification

被动齿轮齿廓采用直线修形，齿顶修形量et2等于零，齿根修形量er2最大.齿向采用抛物线修形，各参数在啮合面上的表示如图6所示.修形曲线方程可以表示成

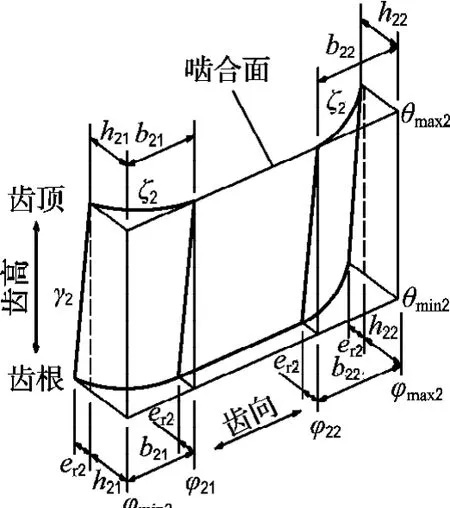
图6 被动齿轮修形示意图Fig.6 Schematic plan of driven gear modification

4 啮合方程的求解方法

4.1 啮合方程的等效解法

将方程组（9）、（10）的求解问题转化为齿面Σ1和Σ2间距离最短及单位法向量偏差最小的优化问题，即

4.2 初值的确定

5 算例分析

根据前面的理论分析，计算了一对齿轮副（见表1）在5组修形参数组合方式下（见表2）的接触迹线和传递误差，如图7和8所示，可见在第Ⅴ组修形参数情况下，接触迹线较为理想.因此将修形参数固定为第Ⅴ组，在轴线偏斜Δγ（2）x、Δγ（2）y分别为3′情况下，考察了轴线平行度误差对接触迹线和传递误差的影响，如图9和10所示.

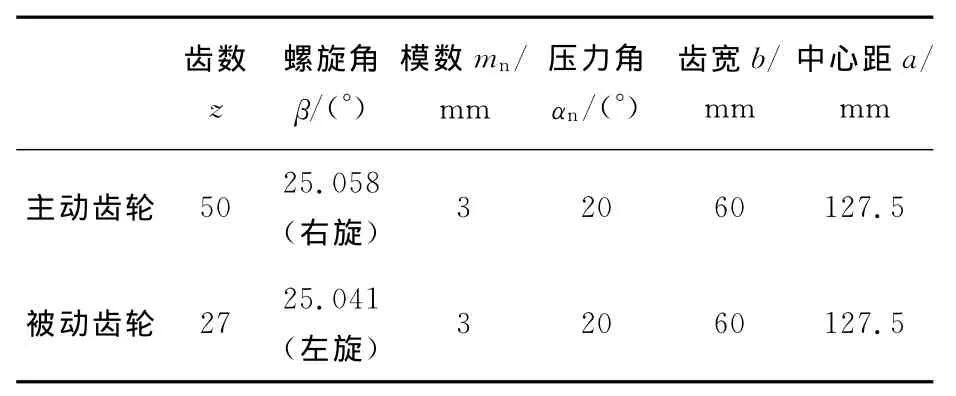
表1 齿轮副几何参数Tab.1 Gear pair parameters

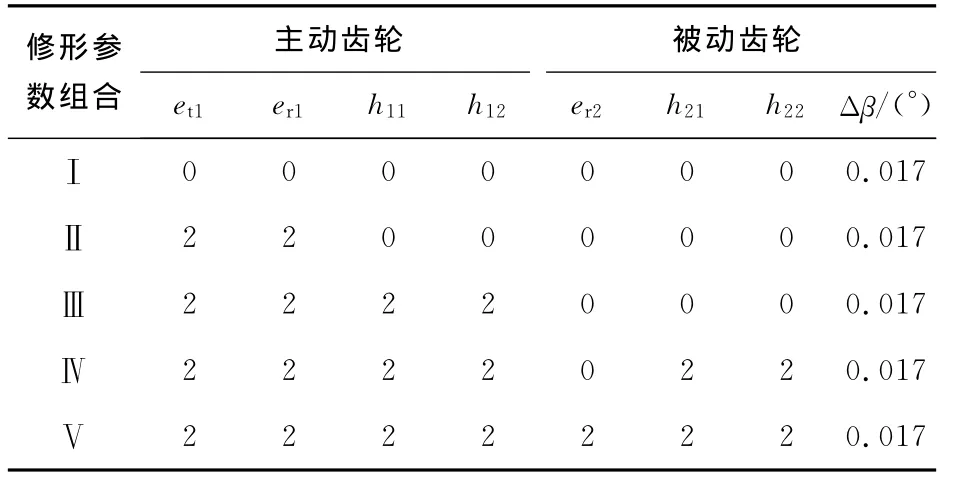
表2 修形参数Tab.2 Modification parameters 10－2 mm

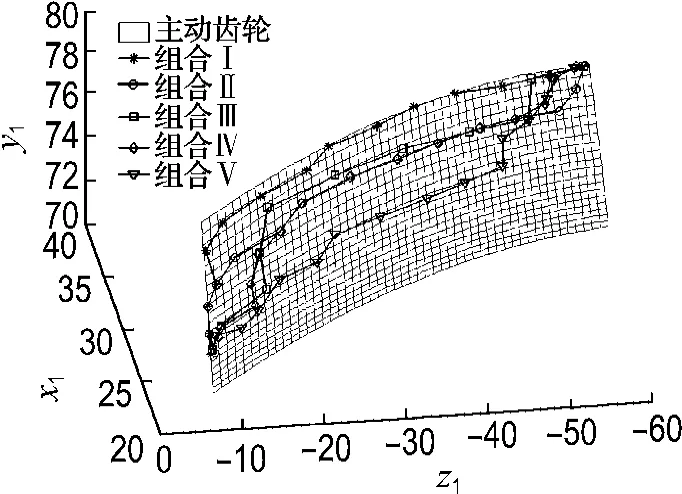
图7 接触迹线Fig.7 Contact path

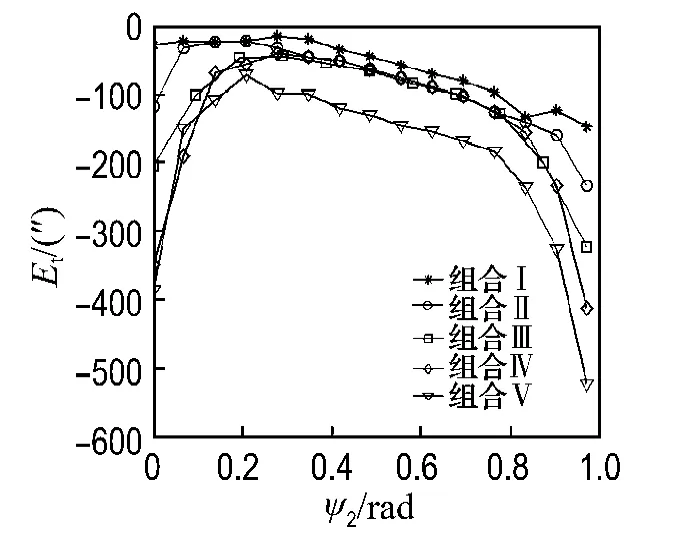
图8 传动误差Fig.8 Transmission error

图9 有轴线偏差情况下的接触迹线Fig.9 Contact path under axial error

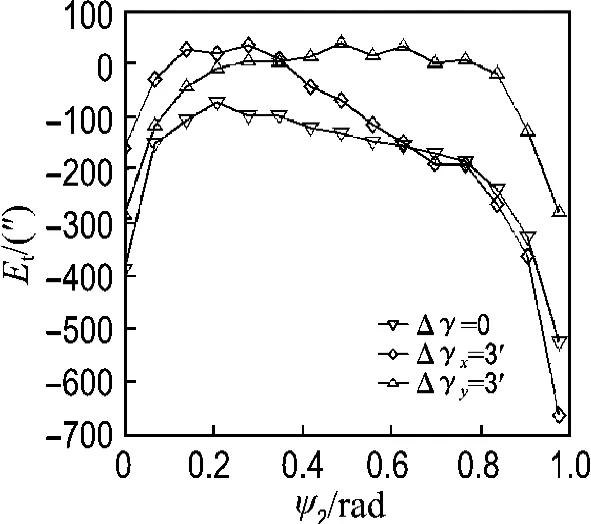
图10 有轴线偏差情况下的传动误差Fig.10 Transmission error under axial error

6 结果讨论

齿轮修形的主要目的是控制接触轨迹、调整传递误差和增强对制造安装误差的适应性.如表2所示，修形参数组合Ⅰ表示被动齿轮进行螺旋角修形，而主动齿轮不修形，在这种情况下，齿轮副沿轮齿边缘接触，传递误差近似呈线性分布，见图7、8曲线修形参数组合Ⅰ.

修形参数组合Ⅱ表示主动齿轮进行齿廓修形，被动齿轮进行螺旋角修形，在这种情况下，接触迹线由齿顶向齿面中间转移，可以消除齿顶边缘接触现象，但齿端仍存在边缘接触现象，见图7曲线修形参数组合Ⅱ.

修形参数组合Ⅲ表示主动齿轮进行齿廓修形和齿向修形，被动齿轮进行螺旋角修形，在这种情况下，接触迹线由齿廓方向转向沿齿轮轴向方向，可以消除齿轮端面边缘接触现象，见图7曲线修形参数组合Ⅲ.

修形参数组合Ⅳ表示在修形参数组合Ⅲ基础上，被动齿轮又进行轴向修形，修形效果也与修形参数组合Ⅲ类似，见图7曲线修形参数组合Ⅳ.

修形参数组合Ⅴ表示在修形参数组合Ⅳ基础上，被动齿轮又进行齿廓修形，在这种情况下，接触迹线进一步向齿面中间转移，接触迹线较为理想，见图7曲线修形参数组合Ⅴ.

由图8可见，齿廓和（或）齿向修形以后，传递误差曲线在啮入侧和啮出侧呈不对称抛物线分布（啮出侧偏大），中间段近似呈线性分布.这样，在受载情况下，有利于减少轮齿啮入和啮出几何干涉，降低振动和噪声［12］.

由图9可见，采用修形参数组合Ⅴ进行齿轮修形以后，在存在轴线偏差的情况下，接触迹线变化不大.

7 结 论

（1）主动齿轮采用齿顶和齿根二次抛物线修形，被动齿轮采用齿根二次抛物线修形和螺旋角修形，可以将接触迹线调整至齿面中间区域，使传递误差曲线呈抛物线分布，有利于改善轮齿啮合状态.

（2）采用前述修形方式，可以降低轮齿啮合对制造和安装误差的敏感性，提高啮合稳定性.

［1］HARIANTO J，HOUSER D R.A methodology for obtaining optimum gear tooth micro－topographies for noise and stress minimization over a broad operating torque range［J］.Gear Technology，2008（7）：42－55

［2］LITVIN F L，LU J，TOWNSEND D，etal.Computerized simulation of meshing of conventional helical involute gears and modification of geometry［J］.Mechanism and Machine Theory，1999，34（1）：123－147

［3］LITVIN F L，CHEN N X，LU J，etal.Computerized design and generation of low－noise helical gears with modified surface topology［J］.Journal of Mechanical Design，Transactions of the ASME，1995，117（2A）：254－261

［4］LITVIN F L，FENG P H，LAGUTIN S A，etal. Helical and spur gear drive with double crowned pinion tooth surfaces and conjugated gear tooth surfaces：US，6205879［P／OL］.2001－03－27.http：／／www.freepatentsonline.com／6205879.html

［5］方宗德.斜齿轮齿面柔度矩阵与修形的有限元计算［J］.航空动力学报，1994（9）：242－244

［6］方宗德.修形斜齿轮的承载接触分析［J］.航空动力学报，1997（12）：251－254

［7］常 山，徐振忠，霍肇波.斜齿圆柱齿轮瞬时啮合刚度及齿廓修形的研究［J］.热能动力工程，1997（4）：270－274

［8］常 山，徐振忠，李 威，等.重载齿轮的最佳轮齿修形［J］.热能动力工程，1995（5）：330－333

［9］WAGAJ P，KAHRAMAN A.Influence of tooth profile modification on helical gear durability［J］.Journal of Mechanical Design，2002，124（3）：501－510

［10］王树人.齿轮啮合理论简明教程［M］.1版.天津：天津大学出版社，2005

［11］UMEYAMA M，KATO M，INOUE K.Effects of gear dimensions and tooth surface modifications on the loaded transmission error of a helical gear pair［J］.Journal of Mechanical Design，1998，120（1）：119－125

［12］LITVIN F L，FUENTES A，GONZALEZ－PEREZ I，etal.Modified involute helical gears：computerized design，simulation of meshing and stress analysis［J］.Computer Methods in Applied Mechanics and Engineering，2003，192（33－34）：3619－3655