《开禧历》定朔计算精度及分析

2011-02-08滕艳辉

自然科学史研究 2011年1期

滕艳辉

(西北大学数学与科学史研究中心，西安 710127)

唐泉

(咸阳师范学院数学与信息科学学院，陕西咸阳 712000;西北大学中国思想文化研究所，西安 710069)

在《开禧历》行用其间，近地点平黄经最小值为269°20'41″，最大值为270°4'54″，可得τ的最大值为0.66°，最小值为0°。于是用式(7)减去式(8)，得到近地点误差δτ近似公式，其形式仍然是分段二次函数。根据其周期性及二次函数的性质，易知其最值出现在x=(180－τ/2)和x=(360－τ/2)时。计算可得，《开禧历》近地点误差最大值是当x=359.77°时，δτ=36.1179，约合 3 分钟;最小值是当 x=179.77°时，δτ= －36.1179。可见，近地点与冬至点的不重合对定朔结果的影响是较小的。从式(7)的形式上也可以看出当太阳中心差按周期变化时，近地点误差也按其周期变化。它是包含在日月改正数误差之中的。

0 引言

“朔”是中国古代历法基本元素之一。人们最早通过平朔来推算朔日，但随着对天文现象的长期观测，发现依照平朔方法所编排的历谱用来计算日月位置以及日月食越来越不能满足人们生产生活和祭祀占卜的需要。为了提高精度，古人对平朔进行日月不均匀性的修正，试图得到真正的朔——定朔。唐代《麟德历》之后的历法，都要给出计算定朔的算法［1］。

对定朔的研究，不仅使我们能够了解中国古代的定朔算法是什么，还具有更重要的意义。通过对历法中定朔的恢复和比较，有助于再现古代历法的精度情况及实用程度，还可以梳理出古代历法在推朔精度上的变化与演进过程，若与同时期其他各文明的精度相比，又可以为客观评价中国历代各部历法在历法史上的地位提供重要依据。日月食的精度很早就受到天文学家和天文史家的关注，但至今没能从数学的角度给出中国古代日月食误差产生的根源。计算定朔是计算日月食的前提，其精度会直接影响日月食的精度［2—3］。搞清定朔精度及误差产生的根源，得出其在日月食计算上的影响，将会为中国古代日月食理论及相关研究提供有用的资料和依据，并为古代天象记录的恢复及其在天文学和地球科学中的应用提供线索［4—5］。

对定朔算法及其相关的研究，引起了一些研究者的高度关注，并做出了重要的工作［6—12］。然而，由于定朔算法被认为是中国古代历法中最简单的算法之一，没能使得很多学者做更深入的研究，在许多地方仍需要有意义的补充。

本文的主旨，是在前人研究工作的基础上，选择宋代最具代表性的历法——《开禧历》，完全依照其推算定朔的过程，编制计算机软件。计算出《开禧历》行用期间任意一个月份的定朔时刻，然后与理论值相比较，统计分析其推算定朔的精度。计算结果中包含有定朔所在日干支及具体时刻信息。比较分析定朔算法理论模型及历法中的定朔算法，结合精度，对其误差的来源进行探讨，找出影响定朔推算误差的根源所在，进而对中国传统历法中的定朔模型做更深入的评价。

1 《开禧历》定朔推步及计算精度

按照古代历法中的思路而建立的定朔算法理论模型由薮内清给出［6］，其表达式如式(1):

式(1)中Tr为定朔时刻，Tp为平朔时刻为太阳改正数为月亮改正数，cs为太阳中心差，而cm则为月亮中心差的相反数。

中国古代的定朔算法在宋代已经发展完善，《开禧历》的定朔算法与主流算法一致，其算法的基本模型是［9］:

《开禧历》是南宋行用时间最长的历法，行用45年［13］。严格按照《开禧历》推算定朔的过程编写计算机程序，并依据其有关常数与数表，可以推算任意一个定朔时刻。现代天文学计算定朔的方法是迭代法，通过三次至五次迭代即能得到很精确的定朔时刻，因此可以将现代计算值看做是真实的定朔值，即理论值。由于用现在的天文引数去计算1000多年前的天文数值，要考虑到地球自转的影响，不同人的计算结果会有些差异，这里采用张培瑜《三千五百年历日天象》［14］中“合朔满月表”所给出的定朔数据。

考虑到利用古代历法计算出的定朔值是以当时帝都或观测台所在的位置为标准的，而张培瑜推算的定朔值采用的是北京时间，即120°E的地方时。为了方便比较，需将所得的定朔时刻转化成依北京时间所表示的时刻。我们推算了《开禧历》行用期间的所有定朔，将其转化为北京时间，并与用现代天文方法计算所得的理论值做比较，得到《开禧历》任意一个定朔的推算误差。

在其545次定朔推算中，误差在0.5小时以下的400次，占73.39%;在1小时以上的仅有16次，而在0.25小时以下的却有250次，占到了45%以上;没有大于2小时的失误推算。误差的最大值为1.8279小时，出现在1211年4月15日这次定朔的推算中。该日入芒种气13日，其下胐朒定数是－1774.842;入转日是2日，入转胐朒定数为－2964.45。其误差平均值为0.1443小时，约合9分钟;误差绝对值的平均值也达到了0.3510小时，约合21分钟，仅比《授时历》的18.4分钟多了不到3分钟。它把我国古代推算定朔的精度又向前推进了一步。《开禧历》推朔误差的分布情况如图1所示。

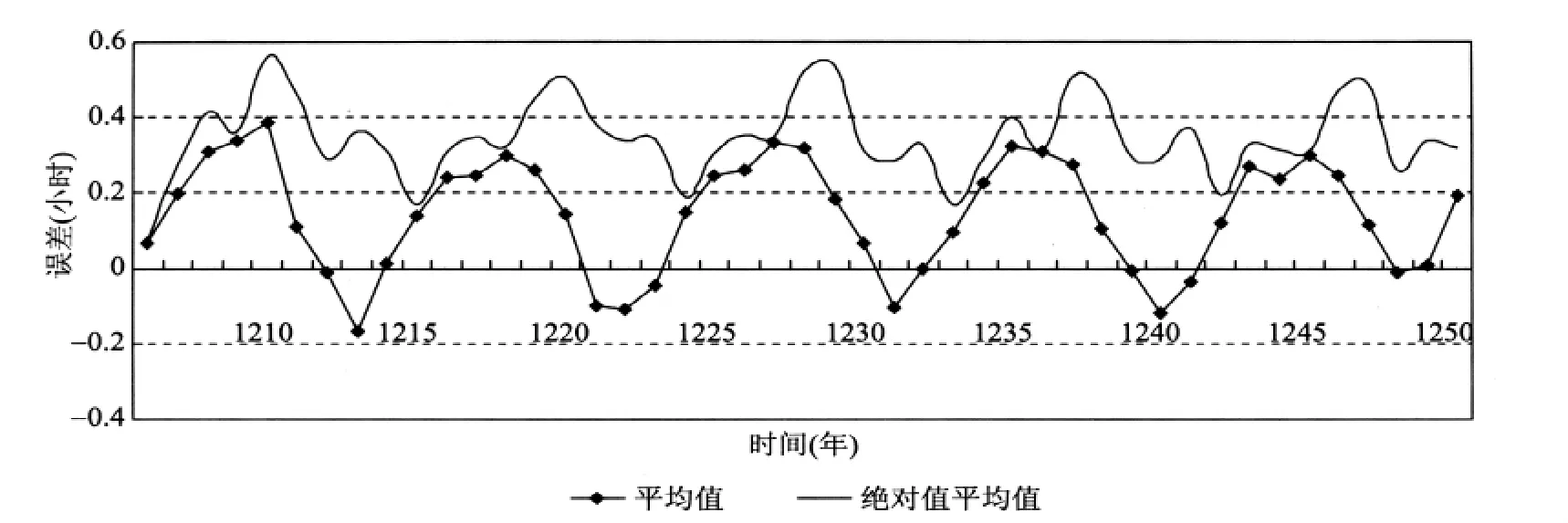
图1 《开禧历》定朔推算误差图

在误差统计中，可以得到一条拟合直线，能够从整体上反映《开禧历》推算定朔精度随时间的变化情况。直线的截距可以代表历法推算误差的初始精度，斜率则反映出历法随时间推移精度逐渐下降的趋势。经计算，其推朔精度每年降低4.5秒左右。《开禧历》行用45年，仍能保持这样的高精度，单从推算定朔方面，可以说它是南宋最好的历法。为了更直观反映《开禧历》行用期间(1208—1251年)定朔误差逐年的变化趋势，我们取每年误差的平均值和绝对值的平均值，其分布情况如图2所示。

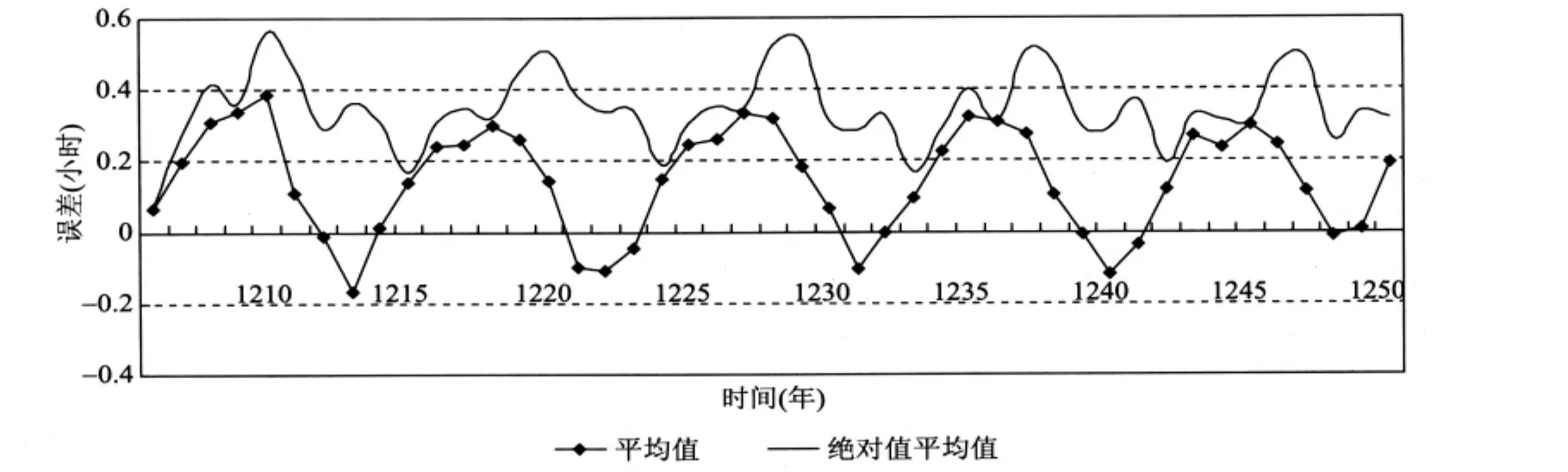
图2 《开禧历》定朔误差逐年变化图

《开禧历》大于0.5小时的定朔误差绝大部分以正值出现，说明其定朔推算先于实际合朔时刻。而且大部分定朔的入转日在二十一日至二十七日之间，说明其定朔算法在此时所做的调整过大，此时的月亮实际速度小于《开禧历》调整后的速度;而此时的太阳又大都运行至春分点与夏至点之间，其大于0.5小时的145次误差中有43次是在此其间。这种误差在随着历法行用时间的增长呈现出更加密集和放大的趋势。

2 《开禧历》定朔误差分析

2.1 定朔误差的周期性

定朔误差会直接影响到日月食的推算。产生误差的因素除去观测本身的影响外，便是对基本天文常数进行的调整和推朔模型本身。观测的误差又与当时的技术水平与设备精度密切相关，不是我们所讨论的范围，而对模型本身所产生的误差进行讨论是必要的。

由式(2)可知，定朔计算的误差来源于以下三项:推算经朔所产生的误差，记为δ0;太阳改正数的计算误差，记为δ1;月亮改正数的计算误差，记为δ2。将式(2)与理论模型式(1)比较，即得定朔误差δ，

式(1)中，如果cs、cm、vs和vm分别表示任意时刻太阳中心差、月亮中心差、太阳的速度和月亮的速度，则定朔可以精确的求出。根据纽康公式，给定任意时刻，上述四个参数亦可方便的求出，即日月改正数是关于时间的函数，这样，最终求出的定朔结果与用现代天文学中的迭代算法所求得的定朔值是一致的。

对于经朔误差δ0，它只与朔望月的长度和经朔起算点有关。根据计算经朔的算法，如果计算的结果大于60，则要用60减之，因此经朔计算结果的取值范围在0到60之间;当用历法计算的经朔值减去理论的经朔值时，如果其误差大于一个朔望月，则要减去一个朔望月。这样，经朔误差在计算过程中会被抵消掉一部分，即以不同的经朔起算点，不同的朔望月长度计算得到的经朔，其误差会保持在一个朔望月之内。因此，经朔误差δ0在理论上是一个周期函数。其误差周期只与朔望月的精度有关，设理论上的朔望月的长度为u*，历法中的朔望月长度为u，则其周期T0可近似表示成

但这个周期是相当长的，在宋代，朔望月的精度在1秒以下，这个周期都会达到几百万年。因此，在对历法精度分析时，经朔误差可以近似为一常数，当作系统误差处理。

考虑到式(2)中的日月改正数Δs和Δm是关于日月中心差的函数，而中心差又是关于时间的函数，这样可以认为日月改正数之和也是关于时间的函数，即任给定一个时间，都可以得到一个改正数值。又太阳改正数Δs是以回归年为周期的函数，月亮改正数Δm是以近点月为周期的函数，则它们的和也是一个周期函数。因这个周期的真实值相当大，在实际应用中，根据需要，利用回归年与近点月的连分数展开，取其渐近分数，得到不同精度的准周期T1。

理论模型中的日月改正数Δs和Δm，如果忽略其长周期及不规则扰动项，则其和Δs+Δm也是关于时间的一元周期函数。如果再忽略回归年的误差与朔望月的误差，则理论模型中的日月改正数之和与历法中日月改正数之和的周期就可认为是一致的。这样对于日月改正数的误差和δ1+δ2也可近似的看成是以T1为周期的周期函数了。定朔误差δ也自然可视为一个周期函数，更近似的，其周期可用日月改正数误差周期T1来表示。

2.2 经朔误差分析

经朔是一个相对的概念，起算点不同，其值差别很大。现代天文学中，已经不再计算经朔，如果需要，则可以取日月平黄经相同的时刻［15］。而宋代历法却是以上元为起算点，然后累加朔望月长度而得到的，这使得用古今两种方式得到的经朔不同。因此用历法推得的经朔值与用现代方法计算的经朔值进行比较是没有意义的，两者的差值并不能反映历法推算经朔的精度，经朔误差也就失去了意义。然而中国古代历法确实是计算经朔的，它对定朔的精度也是有影响的，我们势必要求得它对定朔精度到底起到了多大作用。这样，必须假定理想的上元是存在的，以它为起算点，累加理论的朔望月才能得到理论上的经朔。用历法计算的经朔值与理论值相比较才能得到经朔误差。

求解理论上的上元是很艰难的，而且是不必要的［16］。日月改正数之和是关于时间的周期函数，在一个周期内，由于正负抵消，其函数值的代数和为0。自然，近似的，日月改正数的误差和在其一个周期内的代数和也应该是0。考虑到影响定朔精度的主要因素只有式(3)中的三项，那么若不考虑经朔误差，在我们所计算的误差结果数据中按日月改正数的周期长度选择数据，它们的代数和也应该是0，如果不是，有理由肯定，这些数据的代数和就应该是经朔误差。这样，若忽略回归年、朔望月及近点月的误差，通过连分数展开得到的误差准周期为9年119个近点月，合112个朔望月。《开禧历》的45年数据，也近似以9年为周期波动，与此结果相吻合。我们以周期T1来选取数据，计算其代数和，可以得到历法的经朔误差。

历法行用初期，回归年、朔望月、近点月的误差以及地球自转长期变化的影响是较小的，通过周期法所得到的“经朔误差”更接近于实际情况。经计算，《开禧历》的经朔误差为8.808分钟，占总误差的40%。《开禧历》朔望月常数为29.530591716日，《中国天文年历》提供的某年Y的朔望月长度标准值按下式计算，

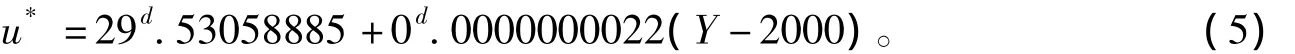
算得《开禧历》朔望月误差为0.3982秒，则其经朔误差会以每年4秒左右的速度减少。这样，除去其朔望月误差的累积值，其行用初年经朔误差的平均值应该是8.4363分钟。误差拟合直线的截距与之很接近，实际上，它就代表了《开禧历》的经朔误差。

2.3 日月改正数误差分析

公式(3)是一个线性关系式，即当日月中心差越大时，所求定朔的误差也就越大，这与图1所显示的结果相吻合。但日月改正数的误差仅会通过对某一次具体的定朔推算来体现其对历法整体精度的影响。若只考查模型本身的精度，则日月改正数的误差计算公式可表示为

日月改正数误差的最小值为太阳和月亮中心差互相抵消，代数和为0时，其误差值也为0;其最大值出现在太阳和月亮中心差同时取最大值时。《开禧历》太阳中心差的最大值为2.36古度，月亮中心差的最大值为5.48古度。而事实上《开禧历》所采用的太阳中心差偏大，据开普勒方程推算的太阳中心差最大值为1.9765度，而月亮中心差最大值的上下限分别为7.75度和5.05度。这样，太阳改正数的最大值为24.10分钟;月亮改正数的最大值为321.00分钟和6.08分钟，取其平均值也达到了122.23分钟。因此，《开禧历》的定朔误差中，日月改正数误差，尤其是月亮改正数误差是最主要的误差。其最大推朔误差为1.8279小时(合109.67分钟)是可以解释的。

中国古代历法基本上把太阳的近地点当作冬至点，这样就使得太阳近地点的平黄经始终选择270°，而且年代越早，近地点平黄经误差越大［17］。为了方便，将《开禧历》的太阳改正数中的“胐朒积”ys近似写作

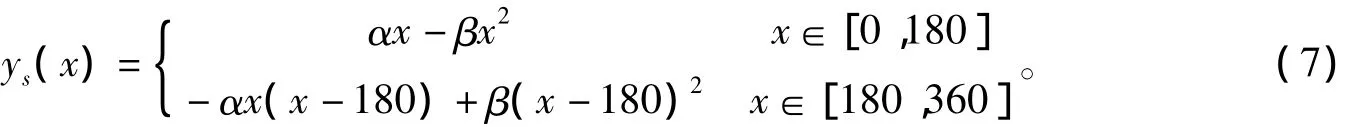
其中x表示太阳平黄经，α、β为待定系数，不同的历法由于日躔表的构造不同会略有差异。经过计算，在《开禧历》中，α、β的取值分别为66.1990和0.3678。若近地点与冬至点相差τ度，则依近地点所得“胐朒积”的近似公式为

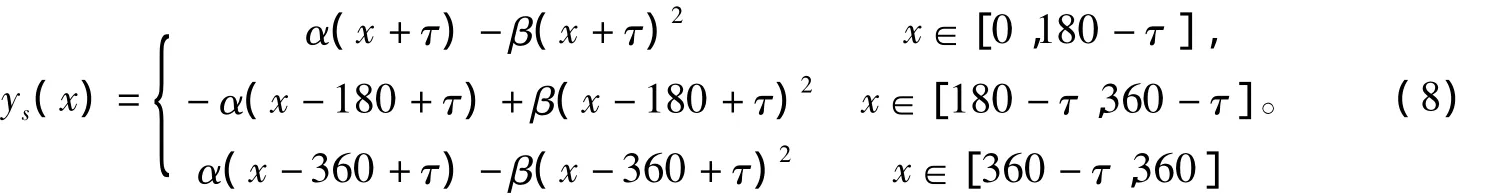
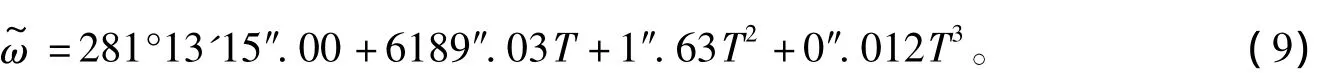
在《开禧历》行用其间，近地点平黄经最小值为269°20'41″，最大值为270°4'54″，可得τ的最大值为0.66°，最小值为0°。于是用式(7)减去式(8)，得到近地点误差δτ近似公式，其形式仍然是分段二次函数。根据其周期性及二次函数的性质，易知其最值出现在x=(180－τ/2)和x=(360－τ/2)时。计算可得，《开禧历》近地点误差最大值是当x=359.77°时，δτ=36.1179，约合 3 分钟;最小值是当x=179.77°时，δτ= －36.1179。可见，近地点与冬至点的不重合对定朔结果的影响是较小的。从式(7)的形式上也可以看出当太阳中心差按周期变化时，近地点误差也按其周期变化。它是包含在日月改正数误差之中的。

2.4 误差综合分析

由于近点月常数与理论值有误差，使得经过累加近点月而求得的入转日数值会有所改变，从而影响月亮改正数的精度。设近点月常数的历法值与理论值分别为g与g*，《开禧历》月离表中每日损益率为φm，其日法为A，则由于近点月常数误差累积导致的月亮改正数误差δg可表示为

类似的，可以得到由于回归年常数误差累积而导致的太阳改正数误差δt为

式中t、t*分别为回归年常数的历法值与理论值，φs为《开禧历》日躔表中的每日损益率。

在表1中，我们给出了各相关因素的影响值。

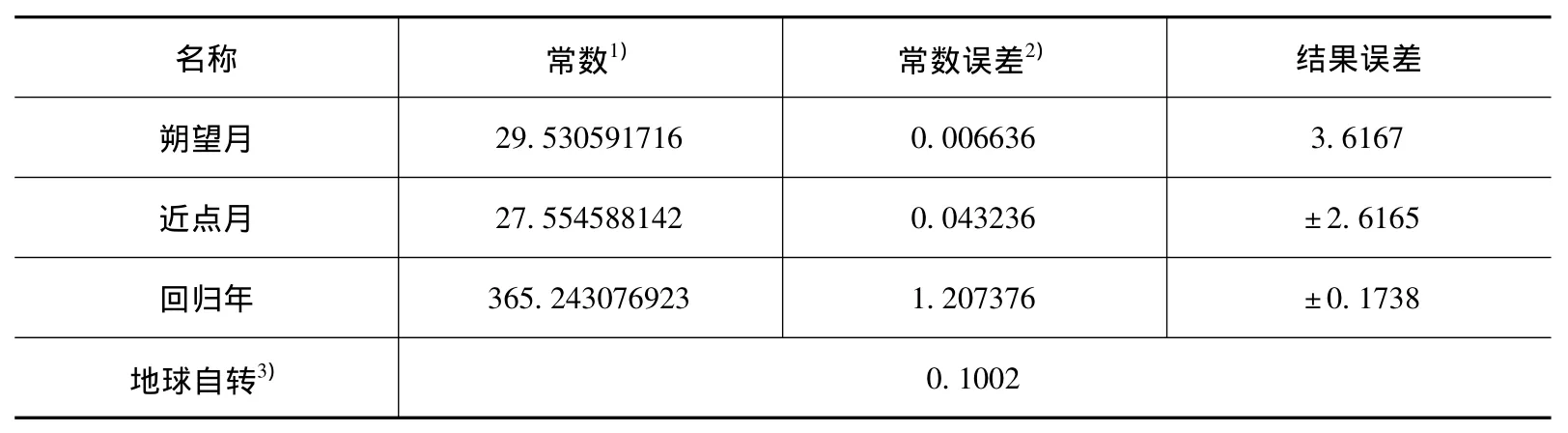
表1 《开禧历》的有关常数及误差

月亮的运动是极其复杂的，存在着规则的与半规则的周期性，而中国古代定朔算法中所用的月亮模型仅仅是以一个近点月为周期，从而进行月离表的设计与入转日的推算。因而在中国古代，人们不能更好的把握月亮运动的真实规律，使得有关月亮的计算误差较大。表1中可以看到，近点月误差是最大的。

月亮运动在一个近点月内的特定时刻与在下一个近点月内的同一时刻的速度并不相同，这样，利用同样的方法得到的“经朔入转”与下一个近点月内的值不同。但中国古代历法只对一个近点月内的月行速度进行调整，而不同近点月之间的月行速度及近点月常数本身并不做修正。如果历法行用时间过长，近点月误差的累积值就会很明显，历法中同一入转日下所对应的月行速度的差异也会加大。不同的入转日下，《开禧历》定朔误差绝对值平均值统计分析如图3所示，可以看到，在近地点附近的调整情况要劣于远地点附近。虽然回归年常数与太阳运行速度也存在着类似影响定朔精度的情况，但一个回归年内太阳中心差的调整是对称的，且太阳中心差的平均误差较月亮的小得多。

图3 不同入转日下的定朔误差平均值

事实上，定朔的误差是经朔误差与日月改正数误差综合作用的结果。经朔误差是影响历法推算精度的重要因素，它使得定朔的推算整体上早于或迟于真朔。但基本天文常数的不精确和对太阳、月亮运动规律的认识不足，降低了历法的精度和实用性。《开禧历》一个朔望月的误差仅为0.3982秒，但45年后，其累积值就会使得推朔迟于真朔近4分钟。有意思的是，如果按此推算，《开禧历》的经朔误差会因此而减小，在其行用150年左右的时候达到最小值，这样，此时的定朔误差也应因此而变的更小。但当我们计算出了《开禧历》1330—1339年近10年的定朔时，其误差绝对值的平均值却增大到了0.4128小时。可以肯定，经朔误差对定朔误差随时间的降低作用要远小于日月改正数误差的作用，尤其是月亮改正数的作用。经朔误差对误差的整体作用是线形的，稳定的，日月改正数误差对每一次的定朔影响是随机的，不稳定的，使得某次推算的定朔值可能会大大偏离真实值，导致推算失误。而在《授时历》以前的历法中，传统的上元积年使得经朔误差难以消除;定朔模型中日月的速度均为平均速度，且存在系数1/vm与1/(vm－vs)的差别;日月的中心差采用完全周期性的数据，使得对日月运行的真实规律把握欠佳;推朔模型本身简单而又粗糙，利用周期形式，不能随时加入修正项来修正。因此，加之基本天文常数的测量误差，历法一旦颁行，使用时间不长便会出现失算，历法家们能做的只是重新调整常数，进而改历。不去改变模型本身和突破推算的基本思想，改后的历法仍不与天合，以致改而再改，造成中国历史上各朝各代的频繁改历。

3 结论

定朔算法在中国古代历法中是一个构造简单但极其重要的算法。历算家往往把推求经朔放在历法的第一部分，在求得日月不均匀性的改正数后，便立即求得定朔。每部历法前面几章内容中很重要的一部分是为“步月离”章中的推求定朔服务的。计算出《开禧历》行用期间的所有定朔时刻，经过时差的修正，转换成依北京时间表示的时刻。与定朔的真实值相比较，得出每一个定朔的推算误差。其推算定朔的总体水平在21分钟左右，最大误差为1.8279小时。

在历法精度对比分析的基础上，分析定朔误差产生的根源。定朔误差可以表示成经朔误差、太阳改正数误差和月亮改正数误差的线性组合。它会表现出一定的周期性特征。如果忽略其中一部分因素，便可以求出定朔误差的准周期。这个值可以近似取为9年或112个朔望月。在一个误差周期内，日月改正数的误差为0，从而可以求出经朔误差。但这种方法在历法行用初期且其行用时间超过9年时适用。

日月改正数误差只会表现为周期性的变化，并没有减小或增大的趋势。其最值仅出现在太阳和月亮同时运行至近地点附近时。近地点误差也呈现出周期性的变化规律，它是包含在日月改正数误差之中的，但对定朔误差的作用较小。在众多影响定朔的误差中，月亮改正数的误差作用最大。在历法的误差拟合直线中，直线的截距实际代表了经朔误差，而斜率则反映了朔望月常数误差值累积的趋势。

经朔误差是每一部历法的固有误差，这与中国传统历法中的上元积年有关。朔望月常数误差会使历法的推算精度随时间的推移而下降。直到《授时历》与《大统历》时，彻底废除了传统的上元积年，使用“岁实消长术”，在推朔模型中使用月亮的即时速度，而不使用平均速度，并对基本天文常数进行更精确的测定，才使得《授时历》与《大统历》共行用了近四百年。

1 (北宋)欧阳修，宋祁，范镇，等．新唐书·律历志［A］．历代天文等志汇编［Z］．第8册．北京:中华书局，1976．559—586．

2 唐泉，曲安京．中国古代的视差理论——以日食食差算法为中心的考察［J］．自然科学史研究，2007，26(2):125—154．

3 Needham J．Science＆Civilisation in China［M］．Cambridge:Cambridge University Press，1959．171．

4 刘次沅．古代交食记录对地球自转速率长期变化的研究进展［J］．天文学进展，1987，5(2):147—157．

5 李勇．中国古历经朔数据的恢复及应用［J］．天文学报，2005，46(4):474—484．

6 薮内清．隋唐历法史の研究［M］．东京:三省堂，1944．61—82．

7 刘金沂，赵澄秋．《麟德历》定朔计算法［A］．薄树人，刘金沂．中国天文学史文集［C］．第3辑．北京:科学出版社，1984．36—88．

8 张培瑜，等．《宣明历》定朔计算和历书研究［J］．紫金山天文台台刊，1992，11(2):121—155．

9 李勇，张培瑜．中国古历定朔推步综述［J］．天文学进展，1996，14(1):66—76．

10 尚晓清，曲安京．《大衍历》定朔算法及程序说明［J］．西北大学学报:自然科学版，1999，29(3):193—196．

11 滕艳辉，王鹏云．《纪元历》等8部宋代历法的定朔推步及精度分析［J］．中国科技史杂志，2009，30(1):55—64．

12 滕艳辉，王鹏云．《纪元历》定朔算法模型及分析［J］．西北大学学报:自然科学版，2008，40(5):855—858．