青藏线上集装箱平车在强横风下的稳定性

高广军，李鹏

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075)

青藏线上集装箱平车在强横风下的稳定性

高广军，李鹏

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075)

采用数值模拟计算的方法，对青藏线上10 m高桥梁上集装箱本身和集装箱车整车在强横风下的气动性能进行研究，得到气动力系数与侧滑角之间的关系；在此基础上，根据静力矩平衡原理建立车辆在轨道上倾覆及集装箱在车体上倾覆的数学模型，得到车辆和集装箱在直线和曲线上运行时车速和临界倾覆风速的关系。研究结果表明：桥梁上集装箱车整车和集装箱自身的横向力系数以及倾覆力矩系数均随着侧滑角的增大而增大；当侧滑角为 75°时达到最大值，之后稍微降低；在低速时，车辆向曲线内侧倾覆的临界风速较低；在高速时，车辆向曲线外侧倾覆的临界风速较低；总体上，集装箱整车和集装箱自身的临界倾覆风速均随着车速的提高而降低，但集装箱在车体上倾覆的临界风速小于车辆整体在轨道上倾覆的临界风速，车辆的限速应当是以集装箱在车体上的倾覆为标准；对于集装箱车整车，当车速分别为0，40，60，80和100 km/h时，整车的临界倾覆风速分别为23.1，20.6，18.5，16.3 和 14.7 m/s。

集装箱车；集装箱；横风；气动性能；倾覆稳定性

我国已修建完成的青藏铁路全长1 142 km，是世界上海拔最高、线路最长、气候最恶劣的高原铁路[1]。青藏高原地区地势开阔，又受到高空强劲西风动量下传的影响，成为全国风速高和大风日数多的地区之一，铁路沿线年大风日为 115～160 d，最大风速为 20～28 m/s[2]，历史上极端最大风速在31 m/s 以上, 西藏安多地区达38 m/s[3]。强横风引起的车辆倾覆事故时有发生[4−6]，给铁路运输和旅客生命财产带来巨大损失。为此，杨明智等[7−10]研究了车辆在大风下的气动性能；高广军等[11−13]研究了客车、货车车辆在强横风下的稳定性；日本、英国、中国颁布了列车在强横风下的管理办法[5,14−15]。上述研究是将集装箱车和集装箱作为一个整体。而集装箱平车结构特殊，集装箱坐落在 4个蘑菇头上，前、后、左、右可以定位，但垂向只能依靠自身的重力来定位。同时，由于集装箱侧墙面积较大，且在空箱情况下自身质量较小，因此，很容易发生集装箱在车体上倾覆或大风将集装箱向上吸起而脱落现象，如1997年兰新线(兰州—乌鲁木齐)上大步—十三间房之间曾发生1辆列车的28个空集装箱被大风连续吹落的现象[16]，2007年北京永定河桥上的集装箱也被大风吹落桥下。集装箱车在横风下的稳定性应当包括整车在强风下的稳定性和集装箱本身的稳定性，而目前对集装箱车的倾覆稳定性研究主要是针对整车进行研究。为了预防青藏线上事故的发生，在青藏线上建立了大风预警与行车指挥系统[17]。对集装箱平车在强横风下的稳定性研究具有重要的应用价值，在此，本文作者以10 m高桥梁上运行的专用集装箱车为例，研究车辆和集装箱自身在强风下的稳定性。

1 集装箱平车气动性能研究

1.1 计算模型

采用数值模拟计算的方法研究集装箱平车在强横风下的气动性能。计算时取集装箱车的宽度l=2.82 m，入口风速vc=60 m/s，空气在 20 ℃时的运动黏度ν=15.08×10−6m2/s，则雷诺数Re=vcl/ν=1.1×107。湍流模型采用κ-ε双方程，流场计算用下述控制方程组来描述。

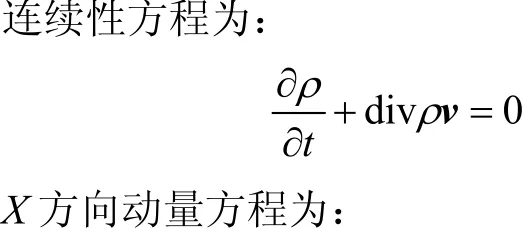
式中：FL为气动升力；FS为气动横向力；M为集装箱或整车的倾覆力矩；ρ为空气密度，在25 ℃时为1.225 kg/m3；U为合成风速；A为集装箱侧向投影面积，A=35.38 m2；H为参考高度，对于集装箱，H=1.4 m，对于整车，H=2.4 m。

1.2 边界条件

采用合成风法对车辆的气动性能进行研究。为了避免来流或尾流的影响，便于设定入口以及出口边界条件，计算区设定为150 m×100 m(长×宽)，见图1。车辆采用4节编组，包括1节机车和3节集装箱车。图1中桥梁上轨面距地面高10 m，区域高80 m。入口风速为合成风速为车速，u为风速，β为侧滑角)。出口设为压力出口，静压为0 Pa；车体、地面以及计算区域上边界均设为无滑移的光滑壁面边界条件。采用三角形单元进行离散，同时对车体表面进行加密处理，以增加计算的准确度。

图1 计算区域Fig.1 Calculation region

1.3 气动力计算结果

计算侧滑角β分别为 0°，30°，45°，60°，75°和90°时10 m高桥梁上集装箱整车和集装箱本身分别受到的横向力、升力和倾覆力矩。其中：集装箱倾覆力矩以集装箱底面中心线外侧0.85 m处为力矩点进行计算；车辆整体的倾覆力矩为背风侧轨道中心线外0.6 m处的力矩。考虑到代表性，选用中间集装箱车的气动力，根据式(1)计算气动力系数，计算结果见图 2和图3。

图2 集装箱的气动力系数与侧滑角的关系Fig.2 Relationship between aerodynamic force coefficients and sideslip angle of container

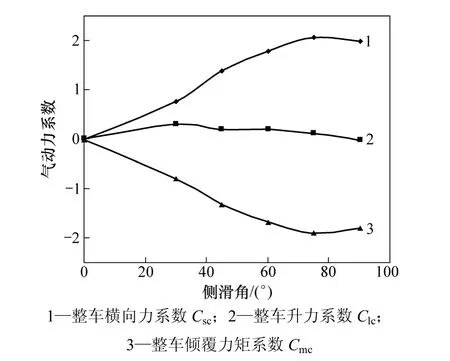
图3 整车的气动力系数与侧滑角的关系Fig.3 Relationship between aerodynamic force coefficients and sideslip angle of whole train

从图2和图3可以看出：集装箱本身和整车的横向力系数和倾覆力矩系数绝对值均随着侧滑角的增大而增大，在侧滑角为 75°时出现拐点；而集装箱气动升力系数在侧滑角为 30°～75°之间基本保持不变，整车的气动升力系数在 30°时出现最大值，之后逐渐降低。同时，气动升力系数远小于横向力系数。其主要原因是：由于集装箱和整车的横截面基本为矩形，车辆的迎风面承受较大的正压且背风面承受较大的负压，因此，横向力较大；而集装箱的底部和顶部均承受负压的作用，两者相互抵消一部分，导致升力较小。对其进行3次曲线拟合，得到气动力系数与侧滑角之间的关系：

式中：Csx，Clx和Cmx分别为集装箱的横向力系数、升力系数和倾覆力矩系数；Csc，Clc和Cmc分别为集装箱整车的横向力系数、升力系数和倾覆力矩系数。上述曲线拟合中，拟合系数R2均大于0.95。

2 车辆倾覆稳定性

2.1 稳定性数学模型

车辆在运行过程中，主要受到气动横向力、气动升力、离心力、车体横向振动惯性力、重力和轮轨力的作用。其中，气动横向力和气动升力的共同作用产生气动倾覆力矩，是导致车辆倾覆的主要因素。根据文献[11−12]，若风由曲线内侧吹向外侧，车辆向曲线外侧倾覆，其计算公式可以表示为：

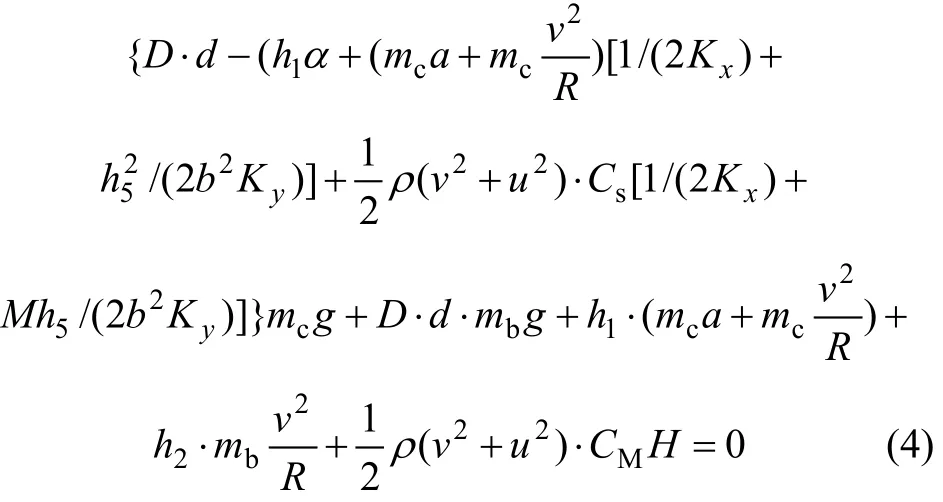
式中：d对于车辆为轮对两侧轮轨接触斑间距的一半，对于集装箱，为集装箱宽度的一半；D为倾覆系数，D=0.8；h1为车体的重心高或集装箱重心高；α为外轨超高角，其值为外轨超高与轮轨接触斑间距之比；mc为车体质量；a为横向振动加速度；R为曲线半径；Kx为车体一侧转向架横向刚度；h5为车辆重心至弹簧支撑面高；b为弹簧悬挂间距的一半；Ky为车体一侧转向架垂向刚度；u为侧风风速；mb为转向架质量；h2为转向架的重心高度。将式(2)或式(3)代入式(4)，可以看出式(4)中仅包含u和v2个未知量，可以得到车速和风速关系曲线。

若风由曲线外侧吹向内侧，车辆向曲线内侧倾覆，则式(4)中倾覆系数D、横向振动加速度a、横向力系数Cs、倾覆力矩系数CM取负号。若车辆在直线上倾覆，则式(4)中的外轨超高角α=0°，曲线半径R→∝。

2.2 集装箱车整车倾覆稳定性分析

由于集装箱车装载1个空6.1 m集装箱时的自身质量较小，最容易发生倾覆事故。这里以此为研究对象，研究集装箱车在大风下的倾覆稳定性。青藏线上线路的曲线半径R最小为600 m，根据式(3)和式(4)，计算得到集装箱车在轨道上倾覆时车速与临界风速之间的关系，见图4。

从图4可以看出：车辆在直线上行驶时，随着车速的提高，临界倾覆风速逐步降低。这主要是因为车辆受到的气动力和横向振动惯性力均随着车速的增加而增加；当风速从曲线内侧吹向外侧时，由于离心力和气动力相互叠加，车辆的临界倾覆风速迅速降低；当风从曲线外侧吹向内侧时，在低速时(车速小于 80 km/h)，由于横向振动惯性力的影响，车辆的临界倾覆风速随车速的提高而降低；在高速时(车速大于 80 km/h)，整车的离心力可抵消部分气动横向力，因此，随着车速的提高，临界倾覆风速逐步提高。由于青藏线上风向变化较大，且车辆有可能在曲线上运行，因此，车辆的车速和临界风速应取图4中3种情况最小值。当车速分别为0，40，60，80和100 km/h时，集装箱的临界倾覆风速分别为 39.1，38.2，36.3，34.4和 33.4 m/s，气动倾覆力矩分别占整个倾覆力矩的90%，98%，94%，90%和90%。

图4 车辆倾覆时车速与风速的关系Fig.4 Relationship between train speed and wind speed when whole train overturns

2.3 集装箱在平车上的稳定性分析

由于集装箱的质量较小，空箱时质量小于4 t，因此，集装箱在平车上的倾覆包括 2种情况：(1) 当集装箱的气动升力大于集装箱的重力时，气动升力可以将集装箱向上吸起，可认为集装箱与车体脱离；(2) 当集装箱的气动升力小于集装箱的重力时，集装箱受到的倾覆力矩使集装箱在平车上倾覆。因此，可首先根据式(2)和式(4)得到集装箱在平车上倾覆时的车辆运行车速与临界风速之间的关系，并根据车速和风速及式(2)计算车辆受到的气动升力，判定车辆受到的气动升力是否大于集装箱的重力。集装箱在车辆上倾覆时车速与临界风速之间的关系见图5。

对图5中不同车速和不同风速下车辆受到的气动升力进行校核，结果表明气动升力均小于空集装箱自身的重力，因此，集装箱在车体上倾覆之前不会被大风吸起。

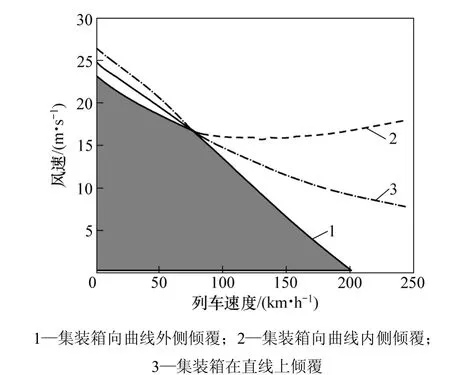
图5 集装箱倾覆时车速与风速的关系Fig.5 Relationship between train speed and wind speed when container overturns

从图5可以看出：集装箱倾覆时车速与风速关系曲线与集装箱整车的车速与风速关系曲线相似：当车辆在直线上运行时，随着车速的增加，临界倾覆风速逐渐降低。若风从曲线外侧吹向曲线内侧，随着车速的增加，车辆的离心力也增加，离心力会抵消部分气动横向力，因此，抵抗车辆向内侧倾覆的能力越强，临界倾覆风速随车速的增加而增加；若风从曲线内侧吹向外侧，此时离心力产生的倾覆力矩随着车速的增加而增加，且离心力和横向气动力相互叠加；因此，随着车速的增加，车辆的临界倾覆风速急剧降低。同理，临界风速应取图5中3种情况的最小值。当车速分别为0，40，60，80和100 km/h时，气动倾覆力矩分别占总倾覆力矩的93%，99%，94%，89%和89%。

2.4 集装箱车的车速与临界风速的关系

由于集装箱车整车在轨道上倾覆和集装箱在车体上倾覆均能引起行车事故，因此，车辆的临界倾覆风速应该取2种情况的最小值。从图4和图5可以看出：集装箱在车体上倾覆的临界风速均小于车辆在轨道上倾覆的临界风速。因此，对集装箱车整车而言，当车速分别为0，40，60，80和100 km/h时，整车处于安全状态的临界风速分别为 23.1，20.6，18.5，16.3和14.7 m/s。

3 结论

(1) 集装箱整车和集装箱在10 m高桥梁上的气动横向力和倾覆力矩均随着侧滑角的增大而增大，在侧滑角为 75°时达到最大值，之后稍微降低；集装箱的气动升力系数远小于横向力系数，且在侧滑角为30°～75°时为常数；车体的气动升力在侧滑角为30°时出现最大值，之后逐渐降低。

(2) 车辆在轨道上倾覆和集装箱在车体上倾覆时其车速和临界风速关系曲线类似。当车辆在直线上运行时，随着车速的提高，临界风速逐渐降低；当风速从曲线外侧吹向内侧时，在低速情况下，随着车速的提高，临界风速逐渐降低，而在高速情况下，由于离心力抵消部分气动力，临界风速逐渐提高；当风速从曲线内侧吹向外侧时，由于离心力和气动力相互叠加，随着车速的提高，临界风速迅速降低。

(3) 气动倾覆力矩是车辆倾覆的主要因素。对于集装箱车整车，整车在轨道上的临界倾覆风速大于集装箱在车体上倾覆的临界倾覆风速，车辆的临界倾覆风速应当取集装箱在车体上倾覆的临界倾覆风速。当车速分别为0，40，60，80和100 km/h时，整车的临界倾覆风速分别为23.1，20.6，18.5，16.3和14.7 m/s。

[1]任建. 青藏铁路客车的几点思考[J]. 铁道车辆, 2003, 41(10):4−8.

REN Jian. Several suggestions on passenger cars for Qinghai—Tibet railway[J]. Rolling Stock, 2003, 41(10): 4−8.

[2]邱道成. 青藏铁路格拉段高原冻土站场设计的特点[J]. 冰川冻土, 2003, 25(Z1): 133−135.

QIU Dao-cheng. The trait of the railway stations and yards design in the permafrost regions of the Qinghai—Tibet railway[J]. Journal of Glaciology and Geocryology, 2003, 25(Z1):133−135.

[3]白虎志, 李栋梁, 董安祥, 等. 青藏铁路沿线的大风特征及风压研究[J]. 冰川冻土, 2005, 27(1): 111−116.

BAI Hu-zhi, LI Dong-liang, DONG An-xiang, et al. Strong wind and wind pressure along the Qinghai—Tibet railway[J]. Journal of Glaciology and Geocryology, 2005, 27(1): 111−116.

[4]葛盛昌, 尹永顺. 新疆铁路风区列车安全运行标准现场试验研究[J]. 铁道技术监督, 2006, 39(4): 9−11.

GE Sheng-chang, YIN Yong-shun. Field test research on safe operation criteria of train in wind region of Lanzhou—Xingjiang railway line[J]. Railway Quality Control, 2006, 39(4): 9−11.

[5]Fujii T, Maeda T, Ishida H. Wind-induced accidents of train/vehicles and their measure in Japan[J]. Quarterly Report of Railway Technical Research Institute, 1999(1): 50−55.

[6]Paul J C, Johnson R W, Yates R G. Application of CFD to rail car and locomotive aerodynamics[C]//Lecture Notes in Applied and Computational Mechanics: The Aerodynamics of Heavy Vehicles II: Trucks, Buses, and Trains. Springer, 2009: 259−297.

[7]杨明智, 袁先旭, 鲁寨军, 等. 强侧风下青藏线列车气动性能风洞试验研究[J]. 实验流体力学, 2008, 22(1): 76−79.

YANG Ming-zhi, YUAN Xian-Xu, LU Zhai-jun, et al.Experimental study on aerodynamic characteristics of train running on Qinghai—Tibet railway under cross winds[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1): 76−79.

[8]周丹, 田红旗, 杨明智, 等. 强侧风下客车在不同路况运行的气动性能比较[J]. 中南大学学报: 自然科学版, 2008, 39(3):554−559.

ZHOU Dan, TIAN Hong-qi, YANG Ming-zhi, et al. Comparison of aerodynamic performance of passenger train traveling on different railway conditions up strong cross-wind[J]. Journal of Central South University: Science and Technology, 2008, 39(3):554−559.

[9]周丹, 田红旗, 杨明智, 等. 强侧风作用下不同类型铁路货车在青藏线路堤上运行时的气动性能比较[J]. 铁道学报, 2007,29(5): 32−36.

ZHOU Dan, TIAN Hong-qi, YANG Ming-zhi, et al. Comparison of aerodynamic performance of different kinds of wagons running on embankment of the qinghai-tibet railway under strong cross-wind[J]. Journal of the China Railway Society, 2007,29(5): 32−36.

[10]周丹, 田红旗, 鲁寨军. 大风对路堤上运行的客运列车气动性能的影响[J]. 交通运输工程学报, 2007, 7(4): 6−9.

ZHOU Dan, TIAN Hong-qi, LU Zai-jun, et al. Influence of strong crosswind on aerodynamic performance of passenger train running on embankment[J]. Journal of Traffic and Transportation Engineering, 2007, 7(4): 6−9.

[11]高广军, 田红旗, 姚松, 等. 兰新线强侧风对车辆倾覆稳定性的影响[J]. 铁道学报, 2004, 26(4): 36−40.

GAO Guang-jun, TIAN Hong-qi, YAO Song, et al. Effect of strong cross- wind on the stability of trains running on the Lanzhou-Xinjiang railway line[J]. Journal of the China Railway Science, 2004, 26(4): 36−40.

[12]高广军, 田红旗, 张健. 横风对双层集装箱平车运行稳定性的影响[J]. 交通运输工程学报, 2004, 4(2): 45−48.

GAO Guang-jun, TIAN Hong-qi, ZHANG Jian. Cross-wind affection on double container train[J]. Journal of Traffic and Transportation Engineering, 2004, 4(2): 45−48.

[13]Carrarini A. Reliability based analysis of the crosswind stability of railway vehicles[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(7): 493−509.

[14]GM/RT2141. Resistance of railwayvehicles to oerturning in gales[S].

[15]乌鲁木齐铁路局. 大风天气列车安全运行办法[S].

Urumchi Railways Bureau. Train safety operation method in wind whether[S].

[16]乌鲁木齐铁路局. 强侧风条件下列车运行安全性现场试验研究报告补充材料[R]. 乌鲁木齐: 乌鲁木齐铁路局, 2006: 4.

Urumchi Railways Bureau. Addition material to research report of field test of train safety operation under strong side wind[R].Urumchi: Urumchi Railways Bureau, 2006: 4.

[17]潘迪夫, 刘辉, 李燕飞, 等. 青藏铁路格拉段沿线风速短时预测方法[J]. 中国铁道科学, 2009, 29(5): 129−133.

PAN Di-fu, LIU Hui, LI Yan-fei, et al. A short-term forecast method for wind speed along golmud-lhasa section of Qinghai—Tibet railway[J]. China Railway Science, 2009, 29(5): 129−133.

(编辑 陈灿华)

Runing stability of container car in Qinghai—Tibet railway line

GAO Guang-jun, LI Peng

(Key Laboratory for Track Traffic Safety of Ministry of Education, School of Traffic and Transportation Engineering,Central South University, Changsha 410075, China)

Numerical simulation was used to research the aerodynamic performance of the train on bridge of 10 m in height in Qinghai—Tibet railway line, and the relationship among the aerodynamic coefficients and the side sliding angle was gotten. The model of the whole train overturning on the track and the container overturning on the train deck was built according to static moment balance, and the relationship between running speed and critical overturning wind of the container car was gotten when they run on straight and curve line. The results show that the side force coefficients and overturning moment coefficients of the whole train and the container increase with the increase of the side sliding angle,and reach the maximum while the side sliding angle is 75° and decrease a little after that. When the train speed is lower,the critical overturning wind speed of train overturning inward the curve is smaller, while when the train speed is higher,the critical overturning wind speed of train overturning outward the curve is smaller. On the whole the critical overturning moment of the whole train and the container decreases with the increase of train speed. The critical wind speed of container overturning on train deck is smaller than that of train overturning on the track, so the train speed operation should be based on the container overturned on train deck. To the whole train, when the speeds are 0, 40, 60, 80 and 100 km/h, the critical wind speeds are 23.1, 20.6, 18.5, 16.3 and 14.7 m/s, respectively.

container car; container; cross wind; aerodynamic performance; overturning stability

U270.1

A

1672−7207(2011)02−0533−06

2009−12−12；

2010−03−01

国家支撑计划项目(2006BAC07B03)

高广军(1973−)，男，河南安阳人，副教授，从事列车空气动力学研究；电话：0731-82655294；E-mail：gjgao@mail.csu.edu.cn