软土中桩基工后长期沉降的预测模型

赵春彦，郑国勇，杨龙才

(1. 中南大学 土木建筑学院，湖南 长沙，410075；2. 同济大学 道路与交通工程教育部重点实验室，上海，201804)

软土中桩基工后长期沉降的预测模型

赵春彦1，郑国勇1，杨龙才2

(1. 中南大学 土木建筑学院，湖南 长沙，410075；2. 同济大学 道路与交通工程教育部重点实验室，上海，201804)

基于软土中桩基工后长期沉降的机理，采用理论分析和工程实际相结合的方法，提出适用于软土中桩基工后长期沉降的预测模型。研究结果表明：提出的预测模型和简化预测模型均可综合考虑地基土体的固结和蠕变，能很好地反映沉降发展的实际情况；但基于土体固结和蠕变对桩基工后沉降的影响程度，对非挤土桩基工后40 d后的实测沉降，可考虑选用简化预测模型进行预测，在其他情况下则宜采用未简化的预测模型进行预测。

桩基；固结；蠕变；工后长期沉降；预测模型

对于软土中的桩基础，因软土具有长期蠕变性质，桩基础的工后沉降是一个漫长的过程。对于大型重点工程，通常都进行桩基的静载试验。桩基的现场静载试验是反映桩基沉降最直接、最可靠的方法，然而，静载试验持续的时间有限，也只能反映桩基工后沉降开始一段时间的情况；因此，如何合理利用观测数据进行桩基沉降的长期预测就显得尤为重要，其预测结果可有效地指导工程设计。传统的沉降预测方法主要有指数方程法、双曲线法、修正双曲线法、对数曲线法、星野模型法、高木俊介法和改进的高木俊介法等[1−5]，这些方法都反映不出影响土体变形的主要因素，预测模型性状和实际土体变形性状差距较大，仅表现为一种形式上的数学拟合，而未考虑实际的沉降机理，常常会出现拟合曲线与实际沉降曲线严重不符的情况，难以实现真正意义上的预测。近年来，灰色预测法、Logistic模型、Compertz模型法、Richards模型法和 Von Bertalanffy模型法等[1−7]由于能较好地反应全过程的沉降与时间的关系，得到广泛应用，但它们也未能综合考虑软土固结和蠕变的综合性质，在结构上仍然存在一些不足。Asaoka模型法[8−9]可以综合考虑软土固结和蠕变的综合性质，但预测过程比较复杂，工程应用不方便。另外，神经网络法[10]目前在沉降预测中也得到了较广泛的应用，但其需要大量的数据作为学习样本，因此，在应用上受到了很大程度的限制。为此，本文作者提出软土中桩基工后长期沉降的预测模型，不仅可以考虑软土固结和蠕变的综合性质，而且结构合理，形式简单，方便于工程的实际应用。

1 模型的提出

软土地基沉降的机理分析如下：在建筑物施工初期，随着上覆荷载的施加，土颗粒孔隙中的水慢慢排出，沉降变形开始发生，当荷载增大到一定程度时，孔隙中水排出速度加快，从而沉降速率也在增大。随着时间的推移，土体中渗流路径加长以及附加应力向下扩散，沉降速率逐渐趋于稳定。宰金珉等[11]基于这个沉降机理提出了一个预测沉降的经验公式即逻辑斯蒂克(Logistic)增长曲线模型，对荷载作用下的地基沉降情形进行了研究，并通过实例加以验证。逻辑斯蒂克曲线的一般形式如下：

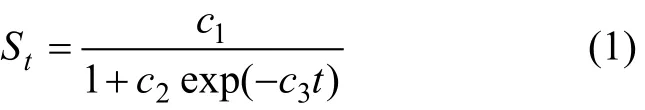
式中：t为沉降的时间；St为时间t时的沉降；c1，c2和c3为待定参数。

因桩基沉降与地基沉降的机理相同，同样都是附加荷载作用下地基土的固结所引起，因此，可考虑将增长曲线模型推广应用到桩基沉降的预测中。但对于软土中的桩基础，由土体蠕变引起的沉降是桩基工后长期沉降不容忽视的部分[12]，因此，软土中桩基的工后长期沉降预测模型应能综合考虑土体的固结和蠕变。

许多室内试验和现场观测结果均表明，土体蠕变与时间对数呈直线关系，常见的计算公式为：

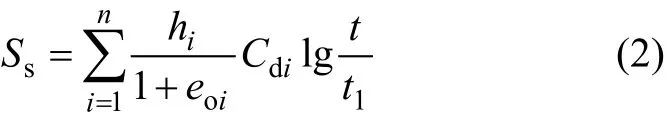
式中：n为划分的土层数；Cd为e−lgt曲线后段的斜率，称次压缩系数；eoi为第i层土的初始孔隙比；Ss为时间t时的蠕变沉降；t1是主固结度为100%的时间，由次压缩曲线上延而得，如图1所示。

图 1 e−lg t曲线Fig.1 Curves of e−lg t

目前关于固结、蠕变的划分争论颇多。由于土体中存在某种结构黏性，蠕变自始至终存在，不可能等到固结完成后压缩才开始。事实上，瞬时沉降、固结沉降和蠕变沉降都是在土体受力后同时发生的，只是某一阶段以一种沉降变形为主。殷宗泽等[13]基于Bjerrum[14]的二维等时e−lgt曲线提出了软土蠕变计算的修正式，其中近似地取t1为1 d。对于桩基的工后沉降，蠕变沉降是其重要的一部分，而在施工期，以土体的固结引起的桩基沉降为主，通常不计蠕变引发的沉降。基于以上认识以及蠕变量和时间的对数正比关系，近似地将蠕变量计算式即式(2)中的t1取为1 d，综合考虑土体固结和桩周土蠕变对桩基工后沉降的影响，将式(1)和式(2)结合起来，提出桩基工后长期沉降的预测模型如下：

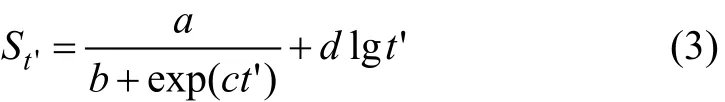
式中：t′为工后沉降的时间，t′＞1；St'是工后时间为t′时的沉降；a，b，c和d为待定常数。

2 参数反演原理与方法

式(3)中的参数a，b，c和d根据实测工后的沉降进行反演优化确定。以沉降计算值和实测值的绝对误差采用最小二乘法原理建立如下目标函数：

参数a，b，c和d的优化取值方法如下：借助于软件OriginPro的非线性曲线拟合(Non-linear curve fit)高级拟合工具(Advanced fitting tool)，运用其中的Origin C语言进行编程，将函数即式(3)嵌入OriginPro中，通过假定参数a，b，c和d的初值，通过多次反复迭代对参数进行反演计算，使目标函数J达到极小值，最终确定参数a，b，c和d的最优化值。

3 实例验证及模型简化

采用软土地基中桥梁桩基的堆载静载试验结果对预测模型进行计算和分析。堆载试验工点位于江苏省昆山市旱泾村—徐公河区间段，属长江三角洲冲积平原区，试验段地基属第四系全新统冲湖积层，表层为黏土，呈灰黄色，软～硬塑，层厚0.76～3.60 m；其下为淤泥质粉质黏土，呈深灰色，流塑，含少量腐植物，局部夹有薄层粉砂，具高压缩性、低强度、高触变性的特点，厚3.2～16.5 m；下卧层为黏土、粉土及粉质黏土，软～硬塑。实例 1采用蕴藻浜特大桥桩基的试验结果，蕴藻浜特大桥桩基设计采用钻孔灌注桩，试验的群桩基础为蕴藻浜特大桥的北京侧桥台，该桥台共12根桩，平面布置呈3排4列方式，实际加载量为12.574 MN，全部加载于2003−12−28完成。以加载完成之日起算桩基的工后沉降，现场试验所得工后沉降随时间发展的沉降如表1所示。实例2采用跨沪宁铁路特大桥521号墩桩基的试验结果，设计采用钻孔灌注桩，该桥墩共10根桩，平面布置呈5排2列方式，实际堆载量为6.137 MN，荷载于2003−12−28加载完成，以加载完成之日算起，现场试验所得工后沉降随时间发展的沉降如表2所示。

实例1采用表1中34～99 d的试验数据，实例2采用表2中57～289 d的试验数据。运用式(3)所示的预测模型反演优化确定参数a，b，c和d，优化的相关系数为：实例1和实例2相应试验数据优化的相关系数)，说明预测模型很好地反映了沉降发展的实际情况。以此对实例1桩基114，128和157 d的沉降进行预测，预测沉降分别为4.72，4.96和5.39 mm；对实例2桩基318，340，375和392 d的沉降进行预测，预测沉降分别为4.02，4.12，4.26和4.32 mm，与试验值接近。模型预测曲线与实测曲线的比较见图2和图3。从图2和图3可以看出：模型预测曲线与实测曲线具有很好的一致性。

在对实例运用预测模型进行参数反演时，发现参数c呈现负值并且绝对值偏大，实例1和实例2参数c最终的取值分别为−36.25和−45.57，而t′＞1，由此不难发现：式(3)的预测模型中的exp(ct′)很小，近乎为0。对于非挤土桩而言，文献[13]指出，由土的固结产生的桩工后沉降较小。对选用的试验沉降来说，实例1和实例2又分别选用的是荷载施加完34 d和57 d以后的沉降，此时，桩周土体的固结已基本完成，因此，在选用此时间以后的沉降进行长期沉降预测时，由桩周土体固结引起的桩基沉降可近似地认为是一定值，即可将a/(b+exp(ct′))视为一定值。基于以上认识，提出桩基工后长期沉降的预测简化模型如下：

表1 蕴藻浜特大桥北京侧桥台桩基工后沉降试验值Table 1 Test values on settlement after construction of pile foundation of Beijing-side abutment of super large bridge named Yun-Zao-Bang

表2 跨沪宁铁路特大桥521#墩桩基工后沉降试验值Table 2 Test values on settlement after construction of pile foundation of 521# pier of super large bridge across Hu-Ning railway

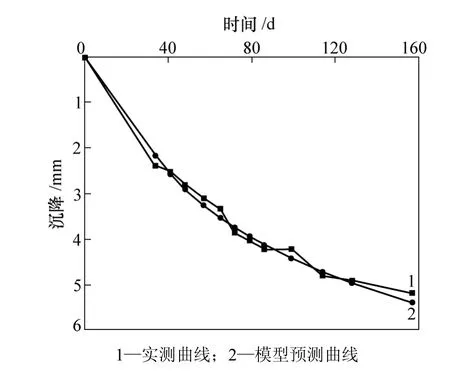
图2 实例1的模型预测和实测沉降曲线Fig.2 Model predicting and testing settlement curves for example 1

图3 实例2的模型预测和实测沉降曲线Fig.3 Model predicting and testing settlement curves for example 2

式中：A和B为待定常数。参数A和B同样采取上述的反演优化方法确定。

同样，实例1采用34～99 d的试验沉降，实例2采用57～289 d的试验沉降，运用式(5)的预测模型反演优化确定参数A和B，优化相关系数为：=0.963 95，＝0.972 25，说明简化预测模型也能很好地反映沉降发展的实际情况。以此对实例 1桩基 114，128和157 d的沉降进行预测，预测沉降分别为 4.64，4.88和5.28 mm，对实例2桩基318，340，375和392 d的沉降进行预测，预测沉降分别为 4.03，4.12，4.27和4.33 mm，与试验值接近，预测结果与实测值的比较见图4和图5。从图4和图5可以看出：简化预测模型与实测曲线也有很好的一致性。

图4 实例1的简化模型预测和实测沉降曲线Fig.4 Simplified model predicting and testing settlement curves for example 1

图5 实例2的简化模型预测和实测沉降曲线Fig.5 Simplified model predicting and testing settlement curves for example 2

以1 a 365 d计算，运用式(5)的预测模型分别对实例1和实例2的桩基长期沉降进行预测，并将式(3)的预测模型的预测结果一同绘于图6和图7中。从图6和图7可以看出：模型和简化模型在对工后长期沉降的预测上均有很好的一致性。为了计算简便，当选用工后一段时间后的实测沉降进行预测，并确定这段时间内土体的固结已基本完成，可选用简化的预测模型；对于非挤土桩，因在施工完后，土体的固结对桩的沉降影响已经很小，选用工后短期时间以后的实测沉降数据为依据(建议工后 40 d，此值是在实例预测过程中，简化预测模型对所选用的工后沉降的适应性不断试预测所得出的1个建议值，预测实例不同，此值会略有不同)，可考虑选用简化预测模型，对工后长期沉降进行预测，比如本文中的算例就可采用简化的预测模型；而对于挤土桩，在很多情况下，施工引起的桩周土体超孔隙水压力在施工完后还将持续很长的时间，对其工后沉降的影响也比较大，因此，需综合考虑土体固结和蠕变对其工后沉降的影响，预测模型采用未简化的模型即式(3)是适宜的。

图6 实例1的模型和简化模型沉降预测曲线Fig.6 Model and simplified model predicting settlement curves for example 1

图7 实例2的模型和简化模型沉降预测曲线Fig.7 Model and simplified model predicting settlement curves for example 2

4 结论

(1) 提出的预测模型与其他预测模型相比，它同时具备了以下2个特点：其一是结构合理，考虑了软土固结和蠕变的综合性质对桩基工后长期沉降的影响；其二是形式简单，参数确定也比较简易，方便于工程的实际应用。

(2) 所提出的预测模型及其相应的简化模型能很好地反映桩基沉降发展的实际情况。

(3) 基于土体固结和蠕变对桩基工后沉降的影响程度，建议：对于非挤土桩基工后40 d后的实测沉降，可考虑选用简化预测模型进行预测，在其他情况下则宜采用未简化的模型进行预测。

(4) 所提出的预测模型和简化预测模型是针对软土中桩基的工后长期沉降而提出的，也可以推广应用到软土地基及软土中其他结构物的工后沉降预测，但对于简化模型，应根据具体情况分析确定其适用性。

[1]王丽琴, 靳宝成, 杨有海, 等. 黄土路基工后沉降预测模型对比研究[J]. 铁道学报, 2008, 30(1): 43−47.

WANG Li-qin, JIN Bao-cheng, YANG You-hai, et al. Contrast study on prediction models of settlement of loess-fill subgrade after construction[J]. Journal of the China Railway Society, 2008,30(1): 43−47.

[2]刘宏, 李攀峰, 张倬元. 九寨黄龙机场高填方地基工后沉降预测[J]. 岩土工程学报, 2005, 27(1): 90−93.

LIU Hong, LI Pan-feng, ZHANG Zhuo-yuan. Prediction of the post-construction settlement of the high embankment of Jiuzhai-Huanglong airport[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(l): 90−93.

[3]彭小云, 叶万军, 折学森, 等. 黄土沟壑区湿软路基沉降预测模型[J]. 交通运输工程学报, 2007, 7(2): 70−75.

PENG Xiao-yun, YE Wan-jun, SHE Xue-sen, et al. Settlement prediction model of wettest-soft loess subgrade in ravine regions[J]. Journal of Traffic and Transportation Engineering,2007, 7(2): 70−75.

[4]LIU Song-yu, JING Fei. Settlement prediction of embankments with stage construction on soft ground[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(2): 228−232.

[5]肖治宇, 陈昌富. 软土路基沉降预测Richards模型方法[J]. 公路交通科技, 2008, 25(11): 29−32.

XIAO Zhi-yu, CHEN Chang-fu. Settlement prediction of soft clay roadbed based on Richards model[J]. Journal of Highway and Transportation Research and Development, 2008, 25(11):29−32.

[6]匡希龙, 邹德强. 基于龚帕斯曲线法的高填方路基工后沉降预测新思路[J]. 公路工程, 2008, 33(1): 127−130.

KUANG Xi-long, ZOU De-qiang. A new thought on prediction method for settlement after construction to high embankment based on Compertz curve method[J]. Highway Engineering,2008, 33(1): 127−130.

[7]王丽琴, 靳宝成, 杨有海. 黄土路堤工后沉降预测新模型与方法[J]. 岩石力学与工程学报, 2007, 26(11): 2370−2376.

WANG Li-qin, JIN Bao-cheng, YANG You-hai. New model and method for forecasting post-construction settlement of loess-fill embankments[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2370−2376.

[8]Asaoka A. Observational procedure of settlement prediction[J].Soils and Foundations, 1978, 18(4): 34−41.

[9]王志亮, 黄景忠, 李永池. 沉降预测中的 Asaoka法应用研究[J]. 岩土力学, 2006, 27(11): 2025−2029.

WANG Zhi-liang, HUANG Jing-zhong, LI Yong-chi. Study on application of Asaoka’s method to settlement prediction[J]. Rock and Soil Mechanics, 2006, 27(11): 2025−2029.

[10]Mohamed A, Shahim M B, Jaksa H R. Artificial neural network-based settlement prediction formula for shallow foundations on granular soils[J]. Australian Geomechanics, 2002,37(4): 45−52.

[11]宰金珉, 梅国雄. 全过程的沉降量预测方法研究[J]. 岩土力学, 2000, 21(4): 322−325.

ZAI Jin-min, MEI Guo-xiong. Forecast method of settlement during the complete process of construction and operation[J].Rock and Soil Mechanics, 2000, 21(4): 322−325.

[12]曾庆有, 周健, 屈俊童. 考虑应力应变时间效应的桩基长期沉降计算方法[J]. 岩土力学, 2005, 26(8): 1283−1287.

ZENG Qing-you, ZHOU Jian, QU Jun-tong. Method for long-term settlement prediction of pile-foundation in consideration of time effect of stress-strain relationship[J]. Rock and Soil Mechanics, 2005, 26(8): 1283−1287.

[13]殷宗泽, 张海波, 朱俊高. 软土的次固结[J]. 岩土工程学报,2003, 25(5): 521−526.

YIN Zong-ze, ZHANG Hai-bo, ZHU Jun-gao. Secondary consolidation of soft soils[J]. Chinese Journal of Geotechnical Engineering, 2003, 5(5): 521−526.

[14]Bjerrum L. Embankments on soft ground[C]//Proceedings Special Conference on Performance of Earth and Earth-Supported Structure. Lafayette: ASCE, 1972: 1−54.

(编辑 杨幼平)

Predicting model on long-term settlement after construction of pile foundation in soft clay

ZHAO Chun-yan1, ZHENG GUO-yong1, YANG Long-cai2

(1. School of Civil Engineering and Architecture, Central South University, Changsha 410075, China;2. Key Laboratory of Road and Traffic Engineering of Ministry of Education,Tongji University, Shanghai 201804, China)

On the basis of mechanism of long-term settlement after construction of pile foundation in soft clay, and combining theoretical analyses with engineering practice, the model applicable to prediction of long-term settlement after construction of pile foundation was put forward. The results show that the predicting model and the simplified predicting model can all take consolidation and creep behavior of soft subsoil into account and reflect the practical situation of settlement development well. But considering influencing degree between consolidation and creep behavior of soft subsoil on the long-term settlement of pile foundation, the application scope of the predicting models are advised. The simplified predicting model may be applied on the condition that actual measuring settlement data after construction for more than 40 d are selected just for non-squeezing pile foundation. As far as other circumstances are concerned, the non-simplified model is appropriate.

pile foundation; consolidation; creep; long-term settlement after construction; predicting model

TU471

A

1672−7207(2011)02−0470−06

2010−01−24；

2010−05−11

铁道部科技发展项目(99G28)

赵春彦(1980−)，男，河南唐河人，博士，讲师，从事基础工程和地下空间的研究；电话：15116437321；E-mail：zcyzbb@163.com