混凝土损伤断裂的三维细观数值模拟

李朝红，王海龙，徐光兴

(1. 西南交通大学 土木工程学院，四川 成都，610031；2. 石家庄铁道大学 土木工程学院，河北 石家庄，050043；3. 河北建筑工程学院 土木系，河北 张家口，075024)

混凝土损伤断裂的三维细观数值模拟

李朝红1,2，王海龙1,3，徐光兴2

(1. 西南交通大学 土木工程学院，四川 成都，610031；2. 石家庄铁道大学 土木工程学院，河北 石家庄，050043；3. 河北建筑工程学院 土木系，河北 张家口，075024)

提出一种在细观层次建立混凝土三维随机骨料随机力学参数模型的方法。将损伤力学与计算力学相结合，基于ANSYS软件平台进行二次开发，建立2组混凝土立方体湿筛试件的数值模型：第1组模型模拟3种不同的骨料随机分布；第 2组模型模拟混凝土各相材料主要力学参数的随机性，分别假定其参数符合对数正态分布和Weibull分布。通过对这 2组模型的轴压进行模拟，揭示混凝土在轴向压力作用下单元的渐进损伤和裂缝的萌生与扩展过程。研究结果表明：数值模拟得到的混凝土立方体抗压强度与试验测得的抗压强度较接近；骨料的随机分布会影响试件裂缝产生的位置和扩展路径，但其对试件承载力的影响不大；混凝土各组成相材料参数的非均匀性降低了试件的极限承载力，采用Weibull分布能较好地表征材料参数非均匀性的影响。

混凝土；损伤断裂；随机骨料；随机力学参数；细观数值模型

混凝土是由水泥砂浆基体和嵌入其中的骨料颗粒所组成的多相复合材料，其物理力学性能复杂多变。长期以来，人们对混凝土的研究主要是基于宏观层次，忽略了混凝土材料内部复杂的细观结构，难以揭示材料变形和破坏的物理机制。大量试验表明，混凝土宏观的破坏行为是细观尺度上的损伤和断裂的累积与发展的结果。由于试验研究的局限性以及现代数值分析技术和高速计算技术的发展，在细观层次上利用数值方法研究混凝土试件的静、动载力学特性，揭示混凝土的破坏机理引起了人们的广泛关注[1−3]。混凝土细观数值模拟不仅能直观反映混凝土细观损伤和裂缝扩展，而且可以通过细观参数的敏感性分析，得出各细观参数对试件极限承载能力的影响。基于细观层次的混凝土数值模型主要有格构模型(Lattice model)[4]、随机粒子模型(Random particle model)[5]、随机骨料模型(Random aggregate model)[6−7]和随机力学特性模型[8]等。Mohamed等[9]基于随机骨料模型，研究了骨料、砂浆、界面材料参数对混凝土荷载位移曲线和裂缝发展模式的影响；Caballero等[10]将骨料视为多面体，骨料与砂浆之间采用零厚度界面单元建立了三维细观模型并利用其进行拉伸数值模拟；刘金庭等[11−12]讨论了模拟混凝土的非均质性所采用的几种随机分布函数概率模型的合理性与适用性。但由于受单元数量和计算机容量的限制，对三维模型研究较少，能够同时考虑混凝土骨料随机分布和材料参数非均匀性影响的三维模型尚未见报道。另外，以往细观模型的建立大多采用自编程序，基于通用结构计算软件建模的并不多，应用性受到限制。在此，本文作者在前人研究的基础上，将损伤力学和计算力学相结合，基于通用结构有限元软件ANSYS，提出一种建立混凝土三维细观随机骨料随机力学参数模型的方法，并对用该方法生成的混凝土试件模型对单轴抗压强度进行数值模拟。

1 随机骨料随机力学参数模型

本文提出的混凝土三维细观随机骨料随机力学参数模型是将混凝土看作由砂浆基质、骨料以及两者之间的界面组成的三相复合材料，采用骨料投影网格法和占位剔除算法实现骨料随机分布，以统计分布加随机赋值的方法表征混凝土各组成相材料参数的非均匀性，分析时引入弹脆性损伤本构模型和最大拉应变破坏准则。

1.1 骨料的模拟及网格剖分

骨料是混凝土的重要组成部分，在混凝土中起骨架和填充的作用，常被模拟成球体、椭球体、凸多面体和任意多面体等几种形式[13]。采用球形骨料，虽然球形骨料会因与实际颗粒形状的差异而产生误差，但已有研究结果表明，其影响可以忽略。在模拟不同级配的混凝土时，骨料的颗粒数根据试件尺寸、骨料级配和骨料所占混凝土的质量比来确定。按照试件骨料级配情况计算出各级骨料颗粒数目，将骨料简化为不同尺寸和数量的球体。常用四级配骨料中小石、中石、大石、特大石质量比为2:2:3:3，三级配骨料中小石、中石、大石质量比为3:3:4，二级配骨料中小石、中石质量比为5.5:4.5。骨料中的小石粒径为5～20 mm，中石为20～40 mm，大石为40～80 mm，特大石为80～150 mm[7]。本文以三级配骨料为例说明数值模型的建立方法，其他级配混凝土试件可参照该方法建模。

在三维空间确定1个球形骨料模型需要有4个变量，即：球体的直径和球心坐标值(X，Y，Z)。这些变量要满足如下要求：

(1) 球体必须在试件轮廓所界定的空间内随机分布，由其球心坐标值来确定位置；

(2) 球心坐标值(X，Y，Z)由一定范围内的随机数分别赋予，从而保证球体在空间分布的随机性；

(3) 这些球心坐标值(X，Y，Z)必须满足两两之间的距离大于2个球体的半径与2倍界面厚度之和，以此来保证产生出来的球体相互独立，不出现位置重叠或交叉；

(4) 球心坐标值(X，Y，Z)到试样各个表面的距离大于其半径与界面厚度之和，以保证产生出来的球体均在试件所定范围之内。

骨料投放前，首先用略小于最小骨料半径长度的尺寸将试件整体剖分为四面体单元，生成均匀的有限元网格，这样，可以保证骨料球心不可能落入有试件边界面的单元。生成骨料单元时，以单元为随机数，采用Monte-Carlo法任意选取1个单元号，并以这个单元的所有节点坐标值的均值为大石球心坐标。在生成第1个大石球心坐标后，通过单元的节点来判断哪些单元在球体内，哪些单元在球边界，哪些单元在球外，剔除那些在球内和球边界的单元。重复以上步骤，直至生成全部大石为止。依此类推，当大石的数目达到要求后，再进行中石的定位，接着是小石定位，这样便将骨料颗粒粒径按照从大到小的原则逐一投放到试件中。程序在寻找骨料空间位置时不会搜索已被剔除掉的单元，可以快速地实现骨料的空间定位，大大提高了运行速度。在生成骨料球心坐标的同时，将判断得到的骨料、砂浆、界面单元直接赋予不同的属性：当单元的所有节点均落入球体内部时，单元为骨料单元；当单元有部分节点落入球体内时，为界面单元；当单元的全部节点都在球体外时，则为砂浆单元。

1.2 界面单元的细分

以上划分网格所采用的单元尺寸接近最小骨料半径，其值相对于界面层厚度大得多，会导致界面层过厚，使得混凝土最关键的细观结构部位失真。为了能够更好地模拟裂缝形态，采用ANSYS中具有细分功能的SOLID45四面体单元对界面单元进行2次细分，并在每次细分后对细分的那部分单元重新判断其材料属性。若单元的所有节点落入球体内部，则单元改为骨料单元；若单元只有部分节点落入球体内，则仍为界面单元；若单元的全部节点都在球体外，则改为砂浆单元。这样，在下一次细分单元时，只需将上一次细分之后仍为界面单元的部分进行细分即可，避免产生过多的非界面细分单元。经过2次界面细分后，骨料表面网格密集，内部则比较稀疏，形成渐变网格，既有效地减少了单元数目，又可体现混凝土的细观构造特征。

1.3 单元材料随机力学参数赋值

从混凝土的细观构成角度看，骨料、界面及砂浆基质三组成相的力学参数与来源地及配比、搅拌过程等多种因素有关。为了考虑混凝土各组成相材料参数的非均匀性，采用统计分布加随机赋值的方法。假定各组成相的材料力学参数如弹性模量、强度等服从各自独立的统计分布规律，由该分布规律产生一个离散的材料力学参数值序列。利用模型中骨料、砂浆基质及界面相单元材料号分别选取各相单元，对于每相单元，将前述生成的该相某一材料力学参数值序列按Monte-Carlo方法随机投放到该相单元中去，从而实现各相单元材料属性的随机力学参数赋值。考虑到骨料单元的材料性质与砂浆和界面单元有所区别(若忽略骨料自身可能存在的节理裂隙等，则每个骨料颗粒的材料可以看做是均质的，而砂浆和界面无此特点)，本文将不同骨料颗粒的材料属性按照假定的随机分布数值序列来赋值，而组成同一骨料的各个单元的材料属性则赋予同一随机数值，砂浆和界面单元的材料参数则直接由随机分布数值序列随机赋值。

本文模型可以模拟多种常用于表征混凝土类脆性材料参数的随机分布，如对数正态分布和 Weibull分布，这2种分布的密度函数如式(1)和(2)所示。

对数正态分布：

1.4 损伤本构模型和破坏准则

大量研究表明：对于混凝土这种准脆性材料,承载后在宏观上呈现出的应力−应变曲线的非线性是细观层次微裂纹的萌生和扩展引起，而不是由于其塑性变形引起；因此，本文采用各向同性弹性损伤本构关系来描述混凝土细观单元各组成相的力学性质[14]。按照Lemaitre应变等价原理，受损材料的本构关系可通过无损材料的名义应力得到，即

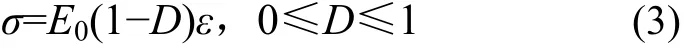
式中：E和E0分别为损伤后的弹性模量和初始弹性模量；D为损伤变量，D=0对应无损状态，D=1对应完全损伤(断裂或者破坏)状态，0＜D＜1对应不同程度的损伤。

按应变等价原理，可以建立单轴拉伸损伤演化方程，在三维应力状态下，通过等效于主拉应变沿用单轴拉伸损伤演化方程。

骨料采用带残余强度的弹脆性损伤本构模型，砂浆和界面由于水泥胶结物具有一定的宏观塑性性质，采用双折线损伤本构模型。

骨料的拉伸损伤演化方程为[8]：

其对应的本构关系曲线如图1所示。

图1 弹脆性损伤本构模型Fig.1 Constitutive model of elastic brittle damage

砂浆与界面的拉伸损伤演化方程为[7]：

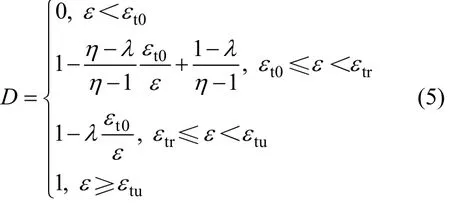
其对应的本构关系曲线如图2所示。

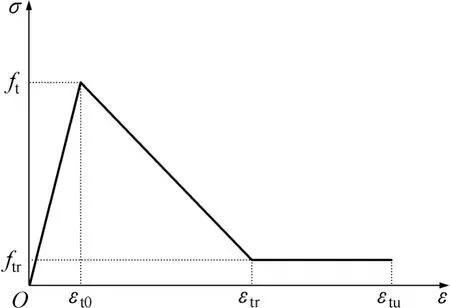
图2 双折线损伤本构模型Fig.2 Damage constitutive model of double broken line

采用最大拉应变准则作为破坏准则，即当细观单元的最大拉伸主应变达到其给定的极限值时，该单元开始发生拉伸损伤。

2 数值模拟

2.1 概况

根据本文提出的建模方法模拟文献[7]中边长为150 mm的立方体湿筛试件进行单轴受压静载试验，该试验测得的极限荷载为26～31 MPa。为了与此试验结果进行对比，数值模型混凝土采用二级配，其中中石直径为30 mm，小石直径为12 mm，小石与中石质量比为5.5:4.5。建立了2组模型：第1组模型研究骨料随机分布对承载力的影响，不考虑材料参数的非均匀性，建立了不同骨料随机分布的3个模型，编号分别为MX1(2)-1，MX1-2和MX1-3；第2组模型研究各组成相材料参数随机分布对承载力的影响，包括第1组模型中的模型MX1(2)-1和以模型MX1(2)-1为基础，令其各组成相材料参数分别满足对数正态分布和Weibull分布建立的2个模型，编号分别为MX2-2和MX2-3。这里重点分析各组成相单元力学参数中弹性模量和强度对混凝土试件承载力的影响。由于泊松比的离散性较小，取为定值[8]。参照文献[7, 15]，2组混凝土试件各组成相材料参数见表1；第1组模型的材料参数取表1中的均值；第2组模型中MX2-2取表1中的均值和变异系数模拟对数正态分布，MX2-3取表1中的均值和均质度模拟Weibull分布。

模型上端面施加垂直方向的受压均布荷载，下端面采用轴向约束，下端面中间点固定。加载步长取1.5 MPa。

模型 MX1(2)-1混凝土三相材料有限元网格见图3，第1组模型的骨料分布情况见图4。

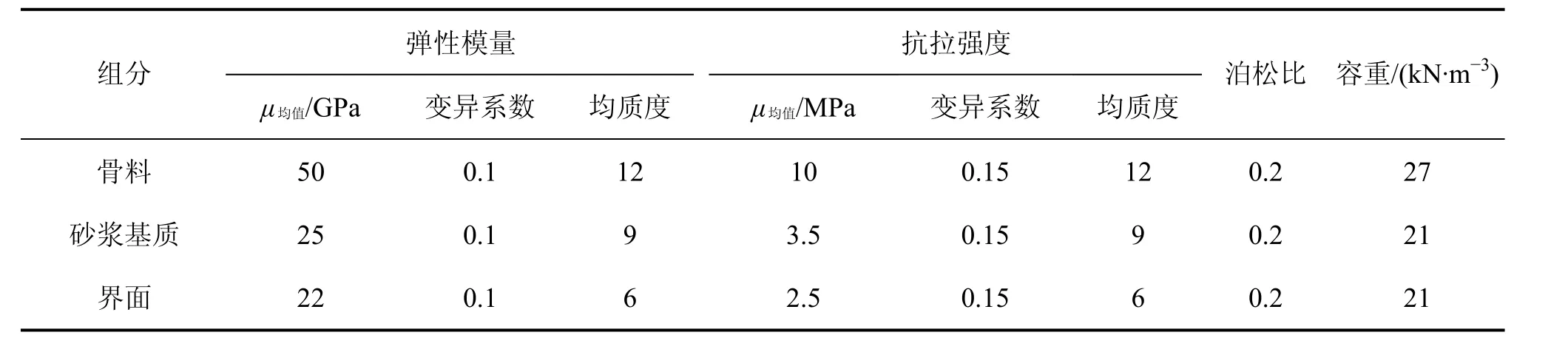
表1 混凝土各组成相材料随机力学参数统计量Table 1 Statistics of random mechanical parameters used to simulate concrete phases

图3 模型MX1(2)-1混凝土三相材料有限元网格Fig.3 Finite element mesh of concrete phases of model MX1(2)-1

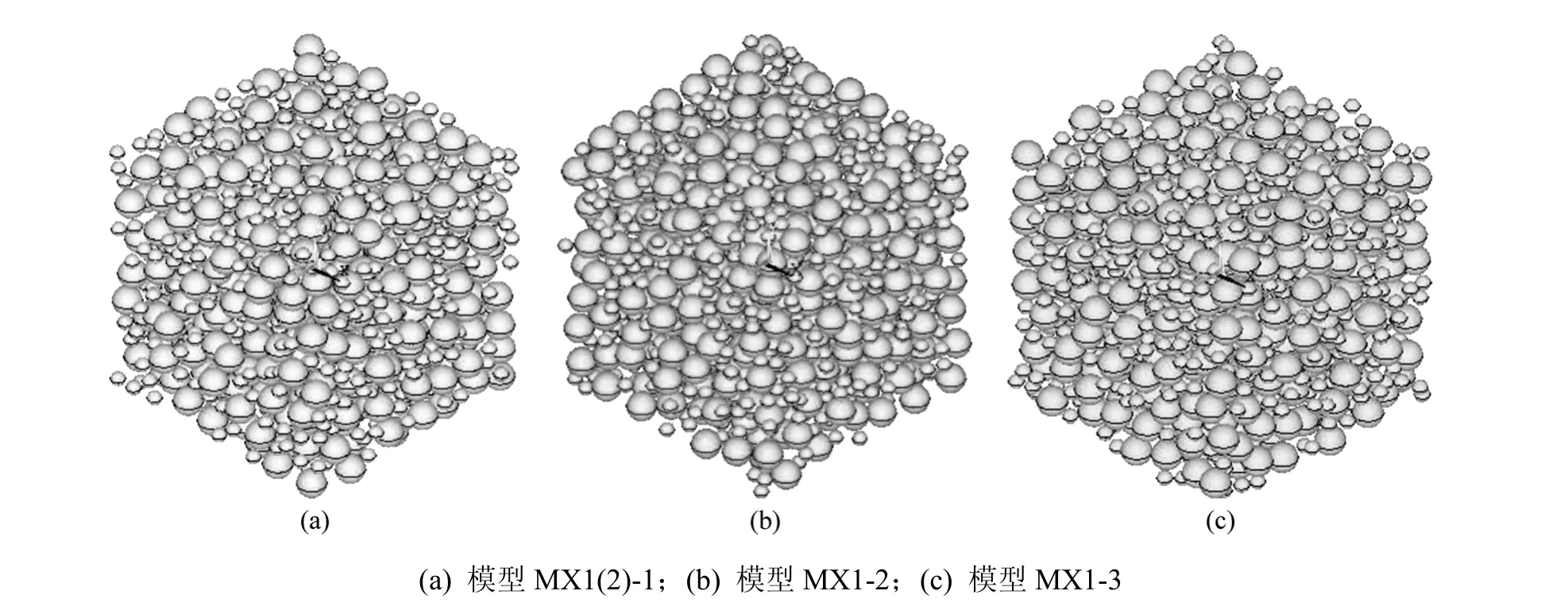
图4 第1组模型骨料随机分布Fig.4 Random aggregate distributing of the first group of models

2.2 结果与分析

第1组模型中模型MX1(2)-1加载至6 MPa时，首先在试件中部出现了少量界面损伤单元，此时试件的竖向位移为0.136 mm；加载至24 MPa时，损伤单元大量增加，主要是界面单元，同时，还有一些砂浆单元发生损伤，损伤的砂浆单元与界面单元连通，与荷载呈 30°～45°方向从试件的中部扩展到两端面，模型变形增加，竖向位移为0.308 mm；当加载至27 MPa时，模型中部开始出现个别界面破坏单元，表示裂缝开始萌生，模型竖向位移增至0.914 mm；当继续加载至33 MPa时，破坏单元大量出现，构件达到极限承载力，最终竖向位移为 2.094 mm。图 5所示为模型MX1(2)-1中部纵剖面切片图所显示的单元渐进损伤过程，其中黑色部分为界面单元，灰色部分为砂浆单元。

从数值模拟结果可以看出：混凝土试件的破坏始于界面单元。由于界面的存在，使得混凝土的抗压强度远低于骨料和砂浆2个主要组成相中任一个的抗压强度；因此，界面可以视为混凝土中的强度限制相。

模型MX1-2和模型MX1-3的承载力分别为35.4 MPa和31.8 MPa。由于骨料分布不同，模型MX1-2和模型MX1-3与模型MX1(2)-1相比，损伤单元开始出现的位置不同，而单元损伤破坏的过程则较相近，这说明混凝土中骨料随机分布会对试件裂缝产生的位置和扩展路径产生影响，因此，导致模型的承载力有所差异，但相差不大。第1组模型的荷载应变曲线见图6。

第2组模型中模型MX2-2和模型MX2-3的承载力分别为26.7 MPa和29.1 MPa，均比按不考虑材料参数非均匀性的模型 MX1(2)-1的承载力低。这主要是由于考虑了各组成相材料参数随机分布后，在承受荷载作用时，模型中各单元受力是不均匀的，形成大量不规则的应力集中点，产生局部单元破坏，导致整个试件承载力降低。其中，材料参数服从 Weibull分布的模型 MX2-3的承载力与文献[7]中试验均值 28.5 MPa更接近，说明Weibull分布能较好地表征混凝土材料参数非均匀性的影响。第2组模型的荷载应变曲线见图7。

图5 模型MX1(2)-1单元渐进损伤破坏过程Fig.5 Gradual damage process of elements of model MX1(2)-1

图6 第1组模型的荷载应变曲线Fig.6 Load-strain curves of the first group of models

图7 第2组模型的荷载应变曲线Fig.7 Load-strain curves of the second group of models

3 结语

(1) 提出的混凝土三维细观数值模型能够实现混凝土骨料的随机分布及其各组成相材料力学参数的概率随机赋值，从而更真实地反映混凝土的非均质性对其力学性能的影响。通过将计算力学与损伤力学相结合，模拟混凝土各组成相单元的渐进损伤破坏及其裂缝的萌生与扩展过程，有利于揭示混凝土损伤断裂机理。

(2) 模型的建立和分析基于通用有限元软件ANSYS平台，结合自编命令流，既具有通用性，又能反映模型自身的特点。引入骨料投影网格法和占位剔除算法，提高了骨料的投放效率；通过界面单元细分处理既优化了细观部位网格，又使单元总数得到控制，实现了三维细观建模，数值模拟结果与试验结果较吻合。

(3) 混凝土中骨料随机分布会影响试件裂缝产生的位置和扩展路径，由此导致试件的承载力略有差异。考虑混凝土各组成相材料参数的非均匀性时，试件的承载力低于不考虑其非均匀性时的承载力，采用Weibull分布能较好地表征混凝土各相材料参数非均匀性的影响。界面作为砂浆基质和骨料颗粒之间的桥梁，是混凝土中最薄弱的环节，对混凝土的强度和裂缝的萌生与扩展起着十分重要的作用。

[1]Chang C S, Wang T K, Sluys L J, et al. Fracture modeling using a microstructural mechanics approach––II. Finite element analysis[J]. Engineering Fracture Mechanics, 2002, 69:1959−1976.

[2]杜成斌, 尚岩. 三级配混凝土静、动载下力学细观破坏机制研究[J]. 工程力学, 2006, 23(3): 125−141.

DU Cheng-bin, SHANG Yan. Study on micro mechanical failure mechanism of the three-gradation concrete under static and dynamic loadings[J]. Engineering Mechanics, 2006, 23(3):125−141.

[3]琚宏昌, 陈国荣, 夏晓舟. 骨料形状对混凝土拉伸强度的影响[J]. 河海大学学报, 2008, 36(4): 554−558.

JU Hong-chang, CHEN Guo-rong, XIA Xiao-zhou. Influence of aggregate shape on tensile strength of concrete[J]. Journal of Hohai University, 2008, 36(4): 554−558.

[4]van Mier J G M, van Vliet M R A. Experimentation, numerical simulation and the role of engineering judgement in the fracture mechanics of concrete and concrete structures[J]. Construction and Building Materials, 1999, 13(1/2): 3−14.

[5]Bazant Z P, Tabbara M R, Kazemi M T, et al. Random particle model for fracture of aggregate or fiber composites[J]. Journal of Engineering Mechanics, 1990, 116(8): l686−1705.

[6]刘光廷. 王宗敏. 用随机骨料模型数值模拟混凝土材料的断裂[J]. 清华大学学报: 自然科学版, 1996, 36(1): 84−89.

LIU Guang-ting, WANG Zong-min. Numerical simulation study of fracture of concrete materials using random aggregate model[J]. Journal of Tsinghua University: Science and Technology, 1996, 36(1): 84−89.

[7]马怀发, 陈厚群, 黎保琨. 混凝土试件细观结构的数值模拟[J]. 水利学报, 2004, 35(10): 27−35.

MA Huai-fa, CHEN Hou-qun, LI Bao-kun. Meso-structure numerical simulation of concrete specimens[J]. Journal of Hydraulic Engineering, 2004, 35(10): 27−35.

[8]唐春安, 朱万成. 混凝土损伤与断裂—数值试验[M]. 北京:科学出版社, 2003: 24−79.

TANG Chun-an, ZHU Wan-cheng. Damage and fracture of concrete numerical test[M]. Beijing: Science Press, 2003: 24−79.

[9]Mohamed A R, Hansen W. Micromechanical modeling of crack-aggregate interaction in concrete materials[J]. Cement &Concrete Composites, 1999, 21(5/6): 349−359.

[10]Caballero A, López C M, Carol I. 3D meso-structural analysis of concrete specimens under uniaxial tension[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(52):7182−7195.

[11]刘金庭, 朱合华, 莫海鸿. 非均质混凝土破坏过程的细观数值试验[J]. 岩石力学与工程学报, 2005, 24(22): 4120−4133.

LIU Jin-ting, ZHU He-hua, MO Hai-hong. Mesostructure numerical test of nonuniformity concrete damage process[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(22): 4120−4133.

[12]梁正召, 唐春安, 张永彬, 等. 准脆性材料的物理力学参数随机概率模型及破坏力学行为特征[J]. 岩石力学与工程学报,2008, 27(4): 718−727.

LIANG Zheng-zhao, TANG Chun-an, ZHANG Yong-bin, et al.On probability model of physico-mechanical parameters of quasi-brittle materials and associated mechanical failure behaviors[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 718−727.

[13]宋玉普. 多种混凝土材料的本构关系和破坏准则[M]. 北京:中国水利水电出版社, 2002: 140−141.

SONG Yu-pu. Constitutive relation and failure criterion of multiple concrete material[M]. Beijing: China Water Conservancy and Electric Power Press, 2002: 140−141.

[14]余天庆, 钱济成. 损伤理论及其应用[M]. 北京: 国防工业出版社, 1993: 132−155.

YU Tian-qing, QIAN Ji-cheng. Damage theory and its application[M]. Beijing: National Defense Industry Press, 1993:132−155.

[15]李建波, 林皋, 陈健云, 等. 混凝土损伤演化的随机力学参数细观数值影响分析[J]. 建筑科学与工程学报, 2007, 24(3):7−12.

LI Jian-bo, LIN Gao, CHEN Jian-yun, et al. Mesoscopic numerical influence analysis of random mechanical parameter of concrete damage evolution[J]. Journal of Architecture and Civil Engineering, 2007, 24(3): 7−12.

(编辑 陈灿华)

3-D mesoscopic numerical simulation of concrete damage and fracture

LI Chao-hong1,2, WANG Hai-long1,3, XU Guang-xing2

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;2. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;3. School of Civil Engineering, Heibei Institute of Architecture and Civil Engineering, Zhangjiakou 075024, China)

On the meso-level, a method for establishing 3-D numerical model with random distribution of aggregate location and mechanical parameters was put forward. Based on damage mechanics and computational mechanics, two groups of numerical models of wet-screened concrete cube specimens were established with ANSYS software, i.e., the first group of models was designed to simulate three kinds of aggregate random distribution with the same gradation, and the second group of models was designed to simulate the random distribution of main material parameters of phases that composed concrete. By the numerical axial compression simulation of the two groups of models, the gradual process of damage crack appearance and the growth of concrete were revealed. The results show that the cubic compressive strength of concrete by numerical simulation approximates to that by physical test. The random distributing of aggregate location has influence on the generating location and expanding paths of crack, yet it has slight influence on the carrying capacity of samples. The material parameters heterogeneity of phases, which can be characterized well by Weibull distribution,reduces the carrying capacity of specimens.

concrete; damage and fracture; random aggregate; random mechanical parameter; mesoscopic numerical model

TU528.01

A

1672−7207(2011)02−0463−07

2009−11−07；

2010−03−28

国家科技支撑计划项目(2006BAJ15B03-01)；石家庄铁道大学科研专项基金资助项目(2010Q18)

李朝红(1974−)，女，河北献县人，博士研究生，讲师，从事混凝土结构的教学和科研工作；电话：13933879681；E-mail：li_zh@126.com