连续组合梁弯矩重分布特征及其随荷载的变化规律

张彦玲，李运生，樊健生

(1. 石家庄铁道大学 土木工程学院，河北 石家庄，050043；2. 清华大学 土木水利学院，北京，100084)

连续组合梁弯矩重分布特征及其随荷载的变化规律

张彦玲1，李运生1，樊健生2

(1. 石家庄铁道大学 土木工程学院，河北 石家庄，050043；2. 清华大学 土木水利学院，北京，100084)

为了对钢−混凝土连续组合梁进行受弯全过程描述，对 3根两跨连续组合梁进行了静力加载试验，研究支座负弯矩区混凝土开裂后组合梁的内力重分布现象，结合试验现象分别确定连续组合梁正负弯矩区弯矩重分布系数随荷载的变化规律，并给出建议计算公式；在此基础上，考虑钢梁与混凝土板之间的相对滑移，采用共轭梁法得到连续组合梁的荷载−挠度和荷载−转角曲线。研究结果表明，连续组合梁弯矩调幅系数随荷载的增加而增加，且在正负弯矩区表现出相同的规律，可以采用弯矩重分布系数的建议计算公式来反映连续组合梁弹性弯矩和混凝土开裂后实际弯矩之间的重分布关系。

组合梁；弯矩重分布；全过程受力分析；滑移；共轭梁法

与简支组合梁相比，连续组合梁具有降低梁高、减小变形和提高承载力等有利因素，综合性能具有很大优势[1−2]，但也存在支点负弯矩区混凝土板易开裂，截面刚度和弯矩分配不协调的缺陷。对连续组合梁进

行受弯全过程受力分析，是研究其整体受力性能和负弯矩区开裂影响的重要途径。全过程受力分析的数值模拟可通过ANSYS等有限元方法实现，但由于模拟过程中涉及非线性迭代收敛，不但计算费时多，而且处于受拉区的混凝土单元，当裂缝超过一定宽度后使单元不再是连续体，无法模拟后续的加载情况，导致很难收敛，一般不易得到荷载−变形曲线的塑性段，在参数分析时也较困难，故采用自编程序来进行连续组合梁的受力全过程及参数分析则更加快捷、方便。荷载−变形全过程曲线通常在已知各截面弯矩−曲率关系的基础上采用共轭梁法[3]来实现。由于连续组合梁负弯矩区混凝土开裂会引起明显的内力重分布现象[4−5]，使负弯矩区弯矩减小，正弯矩区弯矩增大，故其实际弯矩与按弹性方法计算得到的弯矩不同，需要首先根据内力重分布程度的大小确定出各截面的实际弯矩，才能得到截面曲率φ(x)沿梁长度方向的真实分布情况，进而得到组合梁各截面的变形及受弯全过程曲线。弯矩重分布程度可采用弯矩重分布系数表示：

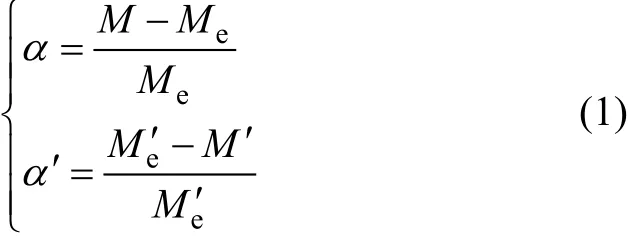
式中： 和 ′分别表示正、负弯矩区的弯矩重分布系数；M和M′分别为实测的正、负弯矩；Me和Me′分别为根据弹性方法计算得到的正、负弯矩。本文作者对钢−混凝土连续组合梁进行了模型加载试验，在其基础上，分别确定了正负弯矩区弯矩重分布系数随荷载的变化规律，并考虑钢梁与混凝土板之间的相对滑移，采用共轭梁法得到了连续组合梁的荷载－变形全过程曲线，与试验结果进行了对比，以期对同类结构的全过程分析提供参考。

1 连续组合梁模型试验

1.1 试验方案

为研究内力重分布和负弯矩区截面的承载力和刚度，对3根两跨连续组合梁(SCB4～SCB6)进行了静力加载试验，其中，SCB5为预应力组合梁，采用折线布置的钢绞线在梁内施加预应力。全部试件的混凝土标号均为C30，板内配筋率为1.347%。按照欧洲规范4(EC4)[6]的规定，钢梁截面均为第Ⅰ类截面，满足塑性设计的要求。SCB4和SCB5在2个梁跨的三分点处用分配梁施加竖向集中荷载，SCB6为单跨加载，各组合梁构造及加载方式见图1(其中：s为栓钉间距)。

图1 SCB4～SCB6构造及加载方式Fig.1 Structure and load conditions of SCB4～SCB6

1.2 内力重分布特征

连续组合梁弹性计算弯矩及由实测支座反力计算得到的截面实测弯矩随荷载的变化情况如图2所示。由图 2可以看出：在试验开始阶段，即荷载在 0.1Pu(Pu为试验梁的极限承载力)之内时，各试件内力与弹性计算结果基本吻合。在这一阶段，混凝土板上表面没有开裂，钢筋与钢梁也均未达到屈服应变，试件具有良好的弹性工作性能。随着荷载的增加，支座截面负弯矩的增加幅度逐渐变小并小于弹性计算弯矩，而跨中正弯矩迅速增加并超过弹性计算弯矩，整个梁表现出了明显的塑性内力重分布现象，且弯矩调幅程度随荷载的增加而增加；当荷载达到或接近极限荷载时，支座截面的钢梁应变迅速增加并超过屈服应变，同时跨中截面的钢梁和混凝土也都超过屈服应变。跨中与支座都形成了塑性铰，结构变为机构，连续组合梁丧失承载力。在这一过程中，支座负弯矩区的转动能力能够保证结构塑性承载能力的充分发挥。

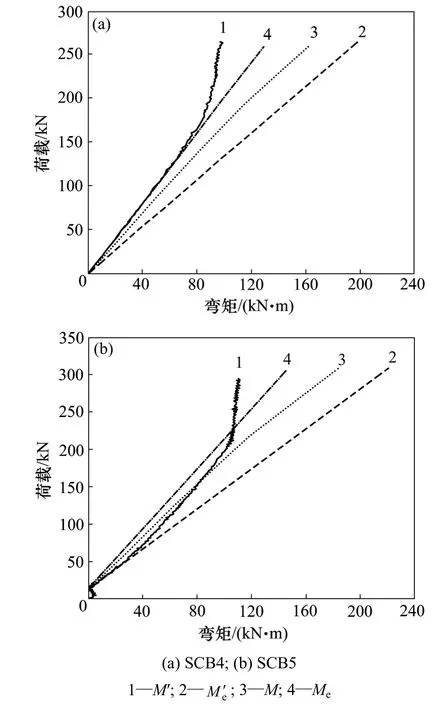
图2 SCB4和SCB5荷载−弯矩图Fig.2 Load−bending moment curves of SCB4 and SCB5

由图2还可见：弯矩重分布系数随荷载的增大而增大，因此，相同荷载水平下由于沿梁轴各截面的弹性弯矩不同，弯矩重分布系数也不同。根据式(1)的定义，连续组合梁SCB4和SCB5支点负弯矩截面和最大正弯矩截面的实测弯矩重分布系数随各自弹性弯矩即荷载的变化规律见图3。图3中，Meu和Me′u分别为最大正弯矩截面和支点负弯矩截面在极限荷载时所对应的弹性弯矩。

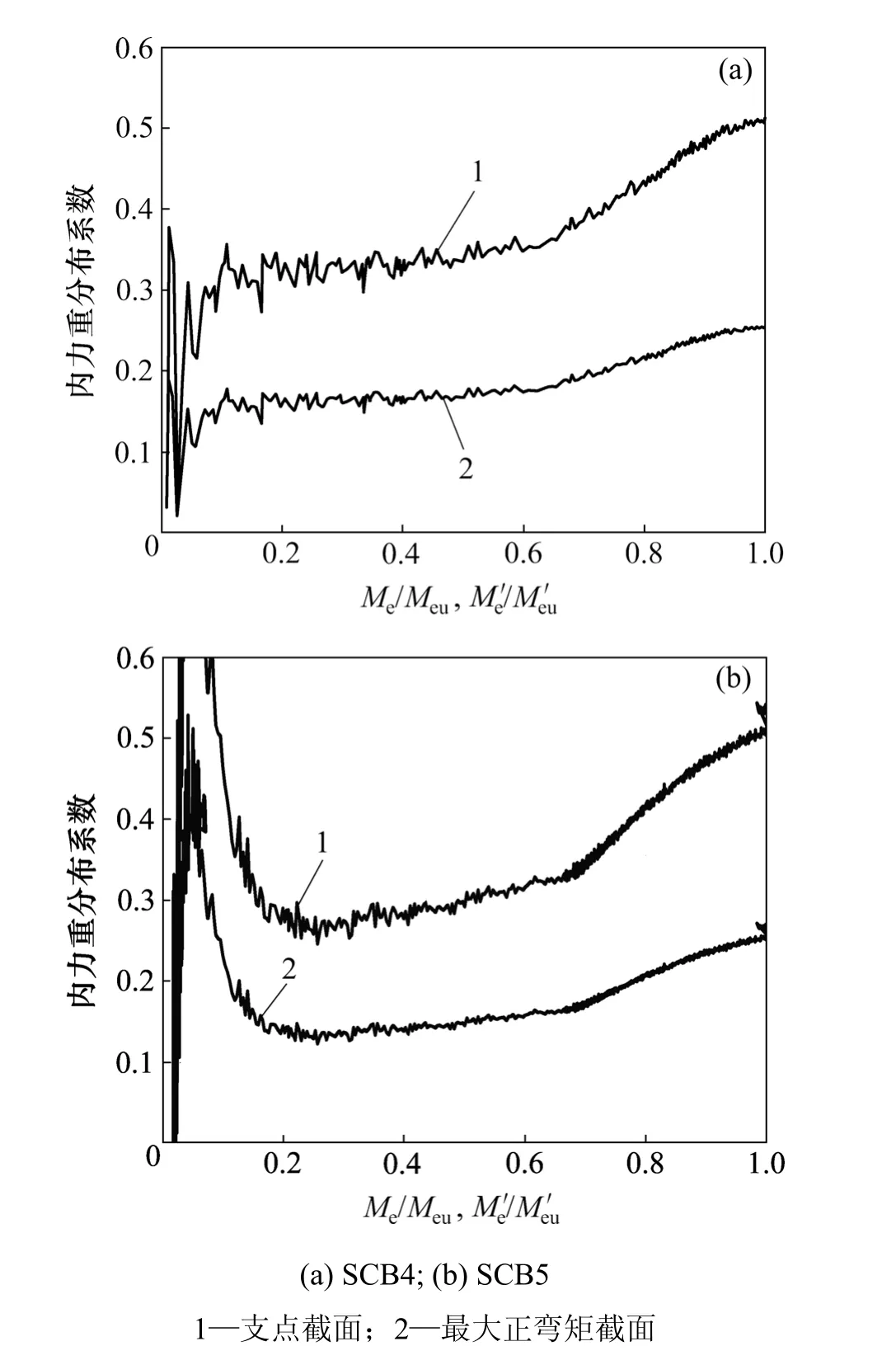
图3 弯矩重分布系数Fig.3 Bending moment redistribution coefficient

2 弯矩重分布系数随荷载的变化规律

2.1 弯矩重分布系数的基本规律

由图3可知：正负弯矩区的弯矩重分布系数表现出相同的规律。由于在荷载较小时测点对读数不是十分敏感，故弯矩重分布系数未显示出明显的规律，但当混凝土开裂以后，规律就比较明显，基本表现为呈直线增大，在屈服弯矩之前，增长幅度较小；在屈服弯矩之后，直线的斜率增大。实际上，在混凝土翼板上表面没有开裂之前，钢筋与钢梁也均未达到屈服应变，故试件具有良好的弹性性能，实际弯矩与弹性弯矩基本吻合，内力重分布程度很小，可忽略不计。经综合考虑，将弯矩重分布系数用分段直线表示，如图4所示。

图4 弯矩重分布系数随荷载的变化Fig.4 Bending moment redistribution coefficient versus load

负弯矩区弯矩重分布系数 ′随荷载的变化规律为：

正弯矩区的弯矩重分布系数的变化规律和式(2)所示的相同，只是相应的弯矩重分布系数分别用αcr，yα和uα表示，其值和负弯矩区的弯矩重分布系数具有相关性。下面首先讨论负弯矩区αc′r，yα′和uα′的取值。

2.2 各控制点弯矩重分布系数的取值

组合梁极限状态时的弯矩重分布系数(即弯矩调幅系数)在各国规范中都有规定，EC4根据组合梁截面的转动能力，按受压区钢梁翼缘和腹板的宽厚比，将组合截面分成4类：

第1类截面：截面能够形成具有塑性分析所需转动能力的塑性铰，截面塑性应变充分发展，抗弯承载力能够达到塑性极限弯矩；

第2类截面：截面的抗弯承载力能够达到塑性极限弯矩，但转动能力受到钢梁局部屈曲的限制；

第3类截面：截面能够达到屈服应力，但塑性抗弯承载力的发挥受到局部屈曲的限制，截面的最大抗弯承载力仅能到达弹性极限弯矩；

第4类截面：不能到达弹性极限弯矩。

当按等刚度梁计算时，EC4规定了支座弯矩重分配的最大容许值uα′：第1类截面(密实截面)uα′=0.4；第2类截面uα′=0.3；第3类截面uα′=0.2；第4类截面uα′=0.1。

式中：Mu′为组合梁支座截面的塑性极限抗弯承载力；B为组合梁正弯矩区考虑滑移效应的组合梁折减刚为组合梁正弯矩区的折减刚度与中支座负弯矩区的刚度之比；1为负弯矩区长度与梁跨L之比；L为连续组合梁跨度。极限塑性转角为：

式中：uφ′为组合梁丧失承载能力时负弯矩区的极限曲率；yφ′为组合梁负弯矩区截面屈服时的曲率；ys1为钢梁下缘至开裂后组合梁换算截面弹性中性轴的距离；ys2为钢梁底部至开裂后组合截面塑性中性轴的距离；Es为钢梁的弹性模量；fsy为钢材的屈服强度；lp2为负弯矩区塑性铰长度，取lp2=1.75h，h为梁高[7]；εsu为钢梁压区极限应变：

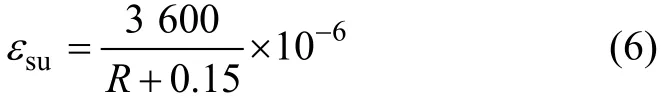
另外，由图3可知：从混凝土开裂至钢筋或钢梁下缘开始屈服的整个过程中，弯矩重分布系数变化很小，且重分布程度不大，故yα′直接取相应于EC4第3类截面极限状态的调幅系数0.2。其原因是当钢筋或钢梁刚开始屈服时，所对应的弯矩正好是弹性极限弯矩，故取0.2；对混凝土刚开裂时弯矩重分布系数αc′r则近似取为第4类截面极限状态的调幅系数0.1，原因与前面的相同。

3 连续组合梁受弯全过程分析

3.1 材料的应力−应变关系

3.1.1 混凝土单轴受压时的应力−应变关系

对于混凝土单轴受压时的应力−应变关系，国内外学者提出了很多理论模型，这里采用我国《混凝土结构设计规范》(GB 50010—2002)[10]给出的应力−应变关系。

3.1.2 考虑受拉刚化效应时混凝土的受拉应力−应变关系

为了模拟组合梁负弯矩区裂缝间的平均弯矩−曲率关系，对钢筋和混凝土之间的相互作用采用受拉刚化模型来近似模拟。文献[11]给出了钢−混凝土组合梁中考虑受拉刚化效应的混凝土受拉应力−应变关系模型，见图5，其中tu为极限拉应变，取混凝土开裂应变的 10 倍[12−13]。

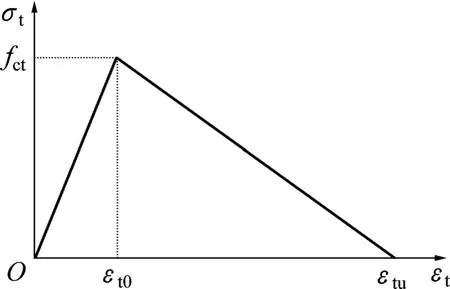
图5 混凝土应力−应变关系的受拉刚化模型Fig.5 Tension stiffness model of concrete stress−strain relation

3.2 组合梁截面内力计算

3.2.1 组合梁截面内力计算方法

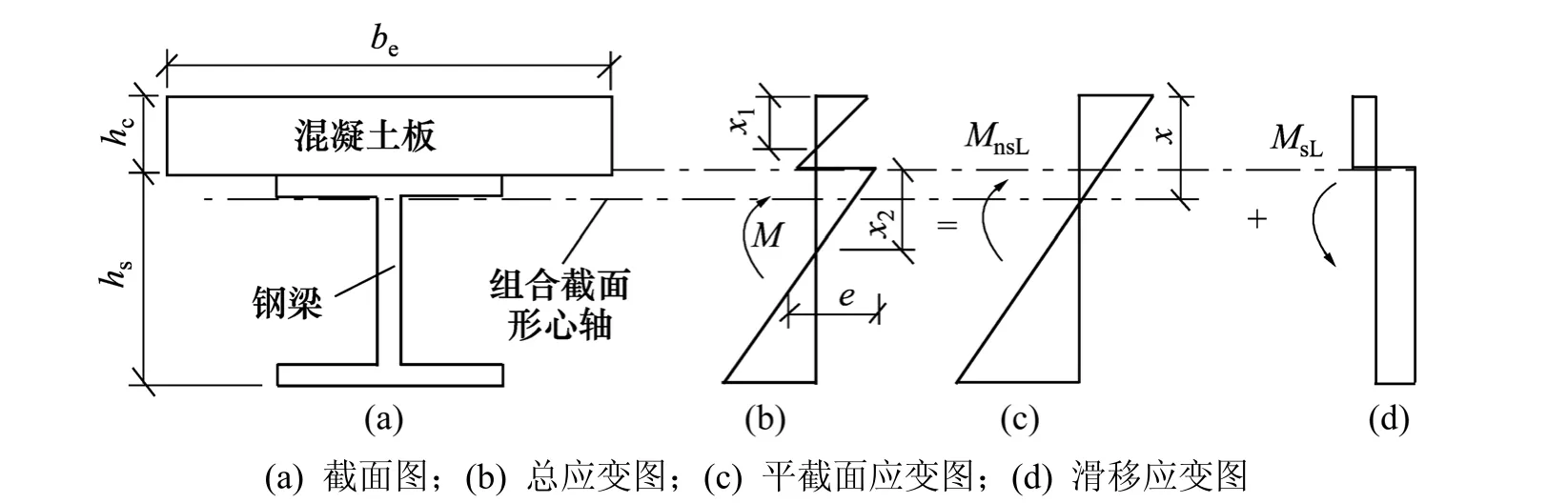
图6 考虑滑移效应后组合梁截面应变示意图Fig.6 Section strain sketch of steel-concrete composite beam considering slip effect

图6所示为考虑滑移效应后组合梁截面的应变图形，其中图 6(c)所示为不考虑相对滑移时按初等梁理论计算出的符合平截面假定的截面应变图形；图6(d)所示为由于栓钉柔性造成的截面滑移应变；图6(b)所示为二者叠加后截面的实际应力图形；hc和be分别为混凝土板的厚度和有效宽度；hs为钢梁的截面高度；e为界面处的滑移应变。从图6可以看出：相对滑移使截面不再符合平截面假定，沿截面高度出现了2个中性轴(距各自上边缘高度分别为x1和x2)，但由于假定滑移引起的混凝土板和钢梁均产生均匀轴向变形，且不考虑二者之间的竖向掀起，故叠加后混凝土板和钢梁具有相同的曲率，且均与不考虑滑移时的截面曲率相同。

根据图6，组合梁最终的截面内力由叠加法得到：

式中：M为考虑滑移后的截面总弯矩；MnsL为不考虑滑移时按初等梁理论计算出的截面弯矩，可根据给定截面的曲率 ，按平截面假定得到换算截面任一点的应变，再由内力平衡积分而得；MsL为由滑移应变引起的截面弯矩，与MnsL方向相反。

3.2.2 对组合梁结合面相对滑移的考虑

对于连续组合梁，将组合梁整体肢解为各同号弯矩范围内的简支梁，在弹性范围内分别计算各等效简支梁任意截面处组合梁界面的滑移应变。

应当说明的是：式(8)只适用于弹性阶段，在此阶段内组合梁界面滑移应变与荷载成正比；而进入塑性阶段后，则不再符合这种规律，但对于完全连接的组合梁，进入塑性阶段后，滑移变形仍然很小，栓钉还远未达到其抗剪强度，故仍可认为组合梁的滑移变形和滑移应变与外荷载呈近似的线性关系，采用式(8)对MsL进行计算时对计算结果影响不大。

3.3 程序编制及试验验证

根据上述原理，采用FORTRAN语言编制了正负弯矩区截面弯矩−曲率(M−φ)全曲线计算程序及连续组合梁的荷载−挠度(P−Δ)和荷载−转角(P−θ)曲线计算程序，得到的连续组合梁SCB4支点负弯矩截面和最大正弯矩截面的弯矩−曲率实测值的比较结果见图7，SCB4荷载与梁端转角的关系曲线及荷载与跨中挠度的关系曲线与试验结果的比较见图8。图8 SCB4荷载−变形关系

图7 SCB4控制截面弯矩−曲率关系Fig.7 Moment−curvature relation of SCB4 at control sections

Fig.8 Load−deformation curves of SCB4

由比较结果可知：2种结果吻合程度较好，验证了上述分析及计算程序的正确性。

4 结论

(1) 随着荷载的增加，连续组合梁表现出明显的塑性内力重分布现象，且弯矩调幅程度随荷载的增加而增加。

(2) 连续组合梁正负弯矩区的弯矩重分布系数表现出相同的规律。在混凝土开裂后，弯矩重分布系数随荷载的增加呈直线增大，在屈服弯矩之前，增大幅度较小；屈服弯矩之后，直线的斜率增大。

(3) 将本文给出的建议公式(2)应用于连续组合梁的全过程受力分析，并考虑组合梁结合面的相对滑移，可得到较好的结果。

[1]聂建国, 余志武. 钢−混凝土组合梁在我国的研究及应用[J].土木工程学报, 1999, 32(2): 3−8.

NIE Jian-guo, YU Zhi-wu. Research and practice of composite steel-concrete beams in china[J]. China Civil Engineering Journal, 1999, 32(2): 3−8.

[2]Johnson R P, Buckby R J. Composite structures of steel and concrete. Vol 2: Bridges[M]. 2nd ed. London: Collins, 1986:2−5.

[3]何政, 欧进萍. 钢筋混凝土结构非线性分析[M]. 哈尔滨: 哈尔滨工业大学出版社, 2007: 216−218.

HE Zheng, OU Jin-ping. Nonlinear analysis of reinforced concrete structures[M]. Harbin: Harbin Institute of Technology Press, 2007: 216−218.

[4]CHEN Shi-ming, JIA Yuan-lin. Required and available moment redistribution of continuous steel−concrete composite beams[J].Journal of Constructional Steel Research, 2008, 64: 167−175.

[5]余志武, 周凌宇, 罗小勇. 钢−部分预应力混凝土连续组合梁内力重分布研究[J]. 建筑结构学报, 2002, 23(6): 64−69.

YU Zhi-wu, ZHOU Ling-yu, LUO Xiao-yong. Study on moment redistribution of steel-partially prestressed concrete composite continuous beams[J]. Journal of Building Structures, 2002, 23(6):64−69.

[6]ENV 1994. Eurocode 4: Design of composite steel and concrete structures[S].

[7]樊健生. 钢−混凝土连续组合梁的试验及理论研究[D]. 北京:清华大学土木水利学院, 2003: 109−111.

FAN Jian-sheng. Experiments and research on continuous composite beams of steel and concrete[D]. Beijing: Tsinghua University. School of Civil Engineering, 2003: 109−111.

[8]Couchman G, Lebet J. A new design method for continuous composite beams[J]. Structural Engineering International, 1996,6(2): 96−101.

[9]聂建国. 钢−混凝土组合结构: 试验、理论及应用[M]. 北京:科学出版社, 2005: 211−217.

NIE Jian-guo. Steel−concrete structure: Test, theory and application[M]. Beijing: Science Press, 2005: 211−217.

[10]GB 50010—2002. 混凝土结构设计规范[S].GB 50010—2002. Design code of concrete structure[S].

[11]LIANG Qing-quan. Strength analysis of steel−concrete composite beams in combined bending and shear[J]. Journal of Structural Engineering, 2005, 131(10): 1593−1600.

[12]Baskar K, Shanmugam N E, Thevendran V. Finite-element analysis of steel−concrete composite plate girder[J]. J Struct Eng,2002, 128(9): 1158−1168.

[13]Liang Q Q, Uy B, Bradford M A, et al. Ultimate strength of continuous composite beams in combined bending and shear[J].J Constr Steel Res, 2004, 60(8): 1109−1128.

[14]郑则群, 房贞政, 宗周红. 预应力钢−混凝土组合梁非线性有限元解法[J]. 哈尔滨工业大学学报, 2004, 36(2): 218−222.

ZHENG Ze-qun, FANG Zhen-zheng, ZONG Zhou-hong. Finite element nonlinear method of prestressed steel−concrete composite beams[J]. Journal of Harbin Institute of Technology,2004, 36(2): 218−222.

[15]张彦玲, 李运生，季文玉. 钢−混凝土简支组合箱梁荷载效应的解析解及剪力滞研究[J]. 石家庄铁道学院学报, 2009, 22(1):5−14.ZHANG Yan-ling, LI Yun-sheng, JI Wen-yu. A closed-form solution of load effect and study of shear lag effect for simple steel-concrete composite box beam[J]. Journal of Shijiazhuang Railway Institute, 2009, 22(1): 5−14.

[16]张彦玲. 钢−混凝土组合梁负弯矩区受力性能及开裂控制的试验及理论研究[D]. 北京: 北京交通大学土木建筑工程学院,2009: 20−48.

ZHANG Yan-ling. Theoretical analysis and experimental research on behavior and crack control of negative moment zone in steel−concrete composite beams[D]. Beijing: Beijing Jiaotong University. School of Civil Engineering, 2009: 20−48.

(编辑 杨幼平)

Characteristics of bending moment redistribution and changing law with load in continuous composite beams

ZHANG Yan-ling1, LI Yun-sheng1, FAN Jian-sheng2

(1. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. School of Civil Engineering, Tsinghua University, Beijing 100084, China)

In order to describe the whole bending process of continuous steel−concrete composite beams, static model tests were conducted on three continuous two-span composite beams, the behavior of bending moment redistribution after concrete cracking at middle support were studied, the changing law of bending moment redistribution coefficient with load in continuous composite beams was determined based on the model tests, and the calculation formula was suggested.Using this formula, and considering the slip between steel girder and concrete slab, the load−deformation and load−rotation angle curves were plotted by principle of conjugate beam method. The results indicate that the bending moment redistribution coefficient of continuous composite beam increases with the increase of the load, and the redistribution law is the same at both positive and negative moment zone. The redistribution relationship between the elastic moment and actual moment after concrete cracking can be described by the suggested formula of bending moment redistribution coefficient.

composite beam; bending moment redistribution; whole process of mechanical analysis; slip; principle of conjugate beam method

U448.21

A

1672−7207(2011)02−0449−07

2010−02−28；

2010−05−22

国家自然科学基金资助项目(50408001)；河北省自然科学基金资助项目(E2009000893)；河北省高等学校科学技术研究青年基金资助项目(2010277)

张彦玲(1973−)，女，河北吴桥人，博士，副教授，从事组合结构、桥梁结构理论及应用研究；电话：15830191769；E-mail: 06mzhang@163.com