渐开线齿轮啮合碰撞力仿真

黄中华，张晓建，周玉军

(1. 湖南工程学院 机械工程学院，湖南 湘潭，411101；2. 中南大学 机电工程学院，湖南 长沙，410083)

渐开线齿轮啮合碰撞力仿真

黄中华1,2，张晓建2，周玉军2

(1. 湖南工程学院 机械工程学院，湖南 湘潭，411101；2. 中南大学 机电工程学院，湖南 长沙，410083)

为获得渐开线齿轮啮合传动时轮齿碰撞力的变化规律，提出基于动力学仿真的渐开线轮齿碰撞力计算方法。建立一对渐开线齿轮啮合传动的动力学模型，给出基于Hertz接触理论的齿轮啮合传动时轮齿碰撞力的计算方法。对齿轮啮合传动时的轮齿碰撞力、x向碰撞力和y向碰撞力的变化规律及其频谱特征进行仿真研究。仿真结果表明：齿轮啮合传动时碰撞力的幅值波动显著，轮齿从啮入到啮出，碰撞力从0 kN增加到最大碰撞力后又减小至0 kN，具有明显的周期性；碰撞力频谱中会出现齿轮啮合频率的1倍频和2倍频；x向碰撞力和y向碰撞力幅值波动显著，具有相同的频谱特征，相位相差约90°；频谱中出现齿轮的旋转频率和啮合频率，存在明显的调制现象，其中载波为齿轮的啮合频率，调制波为齿轮的旋转频率。

碰撞力；齿轮啮合；仿真

渐开线齿轮是机械设备中广泛应用的一种传动装置。齿轮的强度、刚度和疲劳寿命与齿轮啮合传动时的碰撞力密切相关[1−3]。传统的机械设计通常把齿轮啮合传动过程中轮齿产生的碰撞力视为恒力。由于结构的原因，齿轮在啮合传动过程中啮合刚度会发生周期性变化，导致轮齿碰撞力发生相应变化，进而引起齿轮的冲击和振动[4−7]。为了掌握渐开线齿轮啮合传动时的动力学行为，有必要对齿轮啮合传动时轮齿产生的碰撞力进行研究，以获取轮齿碰撞力的变化规律，为齿轮系统的设计提供相关的技术参数。由于齿轮啮合时轮齿碰撞力波动幅度大、齿轮处于旋转运动状态，导致齿轮啮合传动时轮齿碰撞力的实验测取存在许多困难。随着计算机仿真技术和虚拟样机技术的发展，通过建立齿轮啮合传动的虚拟样机模型，运用动力学仿真方法获取齿轮啮合传动时碰撞力已成为现实[2,8−11]。本文作者拟建立齿轮啮合传动的虚拟样机模型，通过仿真研究获取齿轮啮合传动时轮齿碰撞力的变化规律。

1 仿真模型

图1所示为1对渐开线直齿齿轮啮合传动的动力学仿真模型。在2个齿轮的几何中心施加了旋转运动副，确保2个齿轮在运动时绕轴心旋转，2个齿轮的中心距等于2个齿轮分度圆直径之和的一半，两齿轮的轮齿之间定义了实体对实体的接触力。齿轮材料均为45钢，具体结构参数如表1所示。

图1 齿轮啮合传动动力学仿真模型Fig.1 Dynamic simulation model of gear meshing

表1 齿轮结构参数Table 1 Structural parameters of gears

2 碰撞力计算方法

齿轮在啮合过程中，轮齿因接触产生碰撞力。对于相互接触的2个轮齿，设轮齿间的距离为x，忽略齿轮的弹性波动和运动副的间隙，当x≥0时，两齿轮不发生接触，碰撞力为0 kN；当x＜0时，轮齿发生接触，接触力f与轮齿的啮合刚度、接触变形量、非线性指数、阻尼系数和穿入深度有关，具体计算方法如下：

式中：p为施加在物体上的载荷。

由式(1)～(5)可知：轮齿碰撞力的计算需要确定轮齿的啮合刚度、非线性指数、阻尼系数和最大阻尼时的穿入深度等参数。

3 仿真分析

仿真条件：给小齿轮施加1 r/min的转速。齿轮的弹性模量E1=E2=2×105N/mm2，泊松比ν1=ν2=0.285，根据式(2)可得K=7.5×105N/mm2，根据文献[15−17]可知，碰撞力指数e=1.5，阻尼系数C=10 N·s/mm。

图2所示为齿轮啮合传动时轮齿碰撞力的变化，共给出了5个齿轮接触力的变化曲线。从图2可以看出：轮齿碰撞力变化显著，具有明显的周期性。从轮齿的啮入到啮出，碰撞力经历了一个从0 kN到最大碰撞力再回到 0 kN的过程。碰撞力的变化周期大约为0.04 s，与设定的小齿轮转速相对应。

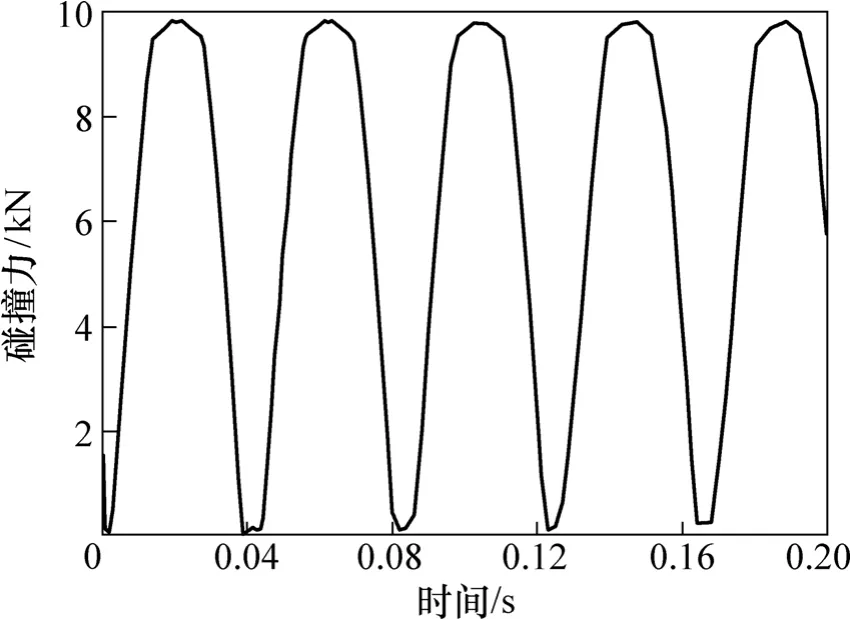
图2 轮齿碰撞力随时间的变化Fig.2 Variation of gear teeth contact force with time

图3所示为齿轮啮合传动时轮齿x向碰撞力的变化。从图3可以看出：x向碰撞力变化显著，波动幅度为0～9.2 kN，碰撞力存在明显的调制现象。图4所示为x向碰撞力的频谱。从图4可以看出有2条幅值突出的谱线：一条是频率为1 Hz的谱线，它对应于小齿轮的旋转频率，另一条是频率为24 Hz的谱线，它对应于小齿轮的啮合频率。由此可见：x向碰撞力的载波频率为齿轮的啮合频率，调制频率为齿轮的旋转频率。

图5所示为齿轮啮合传动时轮齿y向碰撞力的变化。从图5可以看出：y向碰撞力变化显著，波动幅度为0～9.6 kN，碰撞力存在明显的调制现象。图6所示为y向碰撞力的频谱。从图6可以看出有2条幅值突出的谱线：一条是频率为1 Hz的谱线，它对应于小齿轮的旋转频率；另一条是频率为24 Hz的谱线，它对应于小齿轮的啮合频率。对比图3和图5可知：x向碰撞力和y向碰撞力的幅值基本相当，频谱特性相同，区别在于两者存在大约90°的相位差。

图7所示为齿轮啮合传动时齿轮碰撞力的变化。从图 7中可以看出：碰撞力变化显著，波动幅度为0～9.6 kN。图8所示为齿轮碰撞力的频谱。从图8可以看出：在24 Hz处有1条幅值突出的谱线，它对应于齿轮对的啮合频率，在48 Hz处还出现了啮合频率的2倍频。由此可见：齿轮啮合传动时，轮齿碰撞力的频谱特征为频谱图中出现的齿轮啮合频率的1倍频和2倍频。

图3 齿轮x向碰撞力随时间的变化Fig.3 Variation of gear contact force in x direction with time

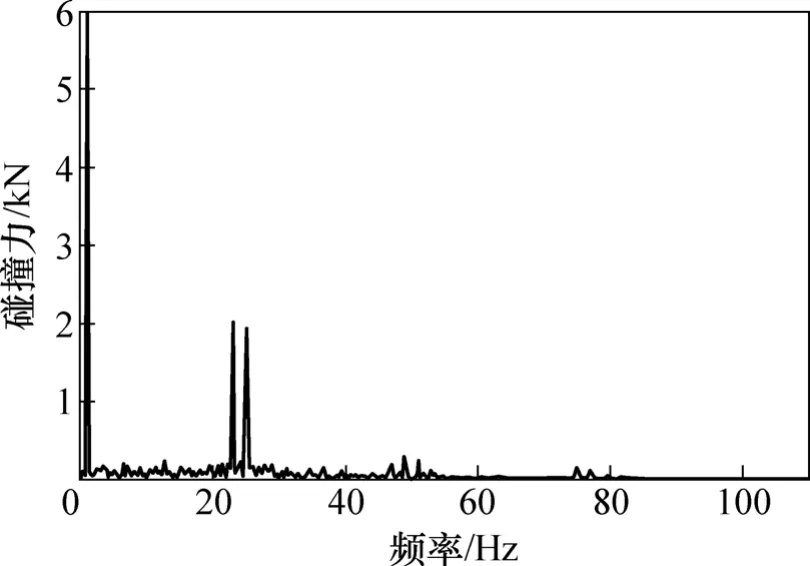
图4 齿轮x向碰撞力频谱Fig.4 Frequency spectrum of gear contact force in x direction

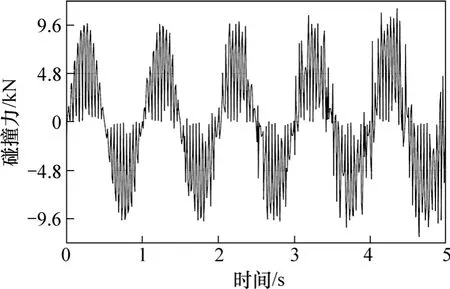
图5 齿轮y向碰撞力随时间的变化Fig.5 Variation of gear contact force in y direction with time

图6 齿轮y向碰撞力频谱Fig.6 Frequency spectrum of gear contact force in y direction

图7 齿轮碰撞力随时间的变化Fig.7 Variation of gear contact force with time

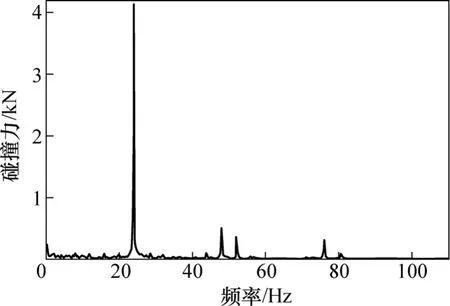
图8 齿轮碰撞力频谱Fig.8 Frequency spectrum of gear contact force

4 结论

(1) 建立了齿轮啮合传动动力学模型，给出了轮齿碰撞力的计算方法，并对齿轮啮合传动时的碰撞力进行了仿真研究。

(2)齿轮啮合传动时碰撞力的幅值波动显著，频谱中会出现齿轮啮合频率的1倍频和2倍频；x向碰撞力和y向碰撞力存在明显的调制现象，具有相同的频谱特征，相位相差约90°。

[1]钟小强, 蒋维, 江磊磊, 等. 冲击载荷下机械压力机齿轮啮合力的仿真研究[J]. 制造技术与机床, 2008(2): 40−42.

ZHONG Xiao-qiang, JIANG Wei, JIANG Lei-lei, et al. Study on the simulation of dynamic meching force of gears under impact load[J]. Manufacturing Technology & Machine Tool, 2008(2):40−42.

[2]毕凤荣, 崔新涛, 刘宁. 渐开线齿轮动态啮合力计算机仿真[J]. 天津大学学报, 2005, 38(11): 991−995.

BI Feng-rong, CUI Xin-tao, LIU Ning. Computer simulation for dynamic meching force of involute gears[J]. Journal of Tianjing University: Science and Technology, 2005, 38(11): 991−995.

[3]占文峰, 杜群贵, 任少云, 等. 渐开线行星齿轮啮合力的动态仿真[J]. 机械设计与制造, 2007(8): 71−73.

ZHANG Wen-feng, DU Qun-gui, REN Shao-yun, et al. A dynamic simulation of meshing force involute planet gears[J].Machinery Design & Manufacture, 2007(8): 71−73.

[4]李润方, 王建军. 齿轮系统动力学: 振动·冲击·噪声[M]. 北京:科学出版社, 1997: 33−45.LI Run-fang, WANG Jian-jun. Gear system dynamics: Vibration,impact and noise[M]. Beijing: Science Press, 1997: 33−45.

[5]Winter H, Gerber H, Muller R. Investigation on the excitation of vibration and noise at spur and helical gears[C]//Proc of 1989 ASME International Power Transmission & Gearing Conference.Chicago, 1989: 765−772.

[6]孙涛, 沈允文, 孙智民, 等. 行星齿轮传动非线性动力学模型与方程[J]. 机械工程学报, 2002, 38(3): 6−10.

SUN Tao, SHEN Yun-wen, SUN Zhi-min, et al. Non-linear dynamic model and equations of planetary gear transmission[J].Journal of Mechanical Engineering, 2002, 38(3): 6−10.

[7]Kahraman A, Singh R. Non-linear dynamics of a spur gear pair[J]. Journal of Sound and Vibration, 1990, 142(1): 49−75.

[8]Parey A, Tandon N. Spur gear dynamics models including defects: A review[J]. The Shock and Vibration Digest, 2003,35(6): 465−478.

[9]Thedossiades S, Natsiavas S. Non-linear dynamics of gear-pair system with periodic stiffness and backlash[J]. Journal of Sound and Vibration, 2000, 229(2): 287−310.

[10]龙凯, 程颖. 齿轮啮合力仿真计算的参数选取研究[J]. 计算机仿真, 2002, 19(6): 87−91.LONG Kai, CHENG Ying. The research of parameters by the simulation of meshing force in gears[J]. Computer Simulation,2002, 19(6): 87−91.

[11]黄泽平, 马吉胜, 吴大林. 齿轮轮齿接触力仿真研究[J]. 机械传动, 2007, 31(2): 26−28.

HUANG Ze-ping, MA Ji-sheng, WU Da-lin. Simulation study of gear tooth contact force[J]. Mechanical Transmission, 2007,31(2): 26−28.

[12]崔清斌, 吴大林, 康海英. 基于ADAMS的齿轮传动系统动态特性仿真[J]. 军械工程学院学报, 2004, 16(5): 9−16.

CUI Qing-bin, WU Da-lin, KANG Hai-ying. Dynamic simulation of gear transmission system based on ADAMS[J].Journal of Ordnance Engineering College, 2004, 16(5): 9−16.

[13]黄泽平, 马吉胜, 李伟, 等. 齿轮副啮合冲击仿真研究[J]. 先进制造与管理, 2006, 25(10): 27−29.

HUANG Ze-ping, MA Ji-sheng, LI Wei, et al. Study on gear pair meshing impact simulation[J]. Advanced Manufacture and Management, 2006, 25(10): 27−29.

[14]李三群, 贾长治, 武彩岗, 等. 基于虚拟样机技术的齿轮啮合动力学仿真研究[J]. 系统仿真学报, 2007, 19(4): 901−904.

LI San-qun, JIA Chang-zhi, WU Cai-gang, et al. Dynamic simulation study of gear meshing based on virtual prototyping technology[J]. Journal of System Simulation, 2007, 19(4):901−904.

[15]李金玉, 勾志践, 李媛. 基于ADAMS的齿轮啮合过程中齿轮力的动态仿真[J]. 设计与研究, 2005(3): 15−17.

LI Jin-yu, GOU Zhi-jian, LI Yuan. A dynamic simulation of meshing force in gear meshing process based on ADAMS[J].Design and Research, 2005(3): 15−17.

[16]田会方, 林喜镇, 赵恒. 基于Pro/ E和ADAMS齿轮啮合的动力学仿真[J]. 机械传动，2006, 30(6): 66−69.

TIAN Hui-fang, LIN Xi-zhen, ZHAO Heng. Dynamic simulation of gear meshing based on Pro/E and ADAMS[J].Mechanical Transmission, 2006, 30(6): 66−69.

[17]李起忠, 刘凯. 基于虚拟样机技术的齿轮啮合力的计算与仿真[J]. 重型机械, 2006(6): 49-51.

LI Qi-zhong, LIU Kai. Calculation and simulation of gear meshing force based on virtual prototyping technology[J]. Heavy Machinery, 2006(6): 49−51.

(编辑 陈爱华)

Simulation of contact force of involute gear meshing

HUANG Zhong-hua1,2, ZHANG Xiao-jian2, ZHOU Yu-jun2

(1. College of Mechanical Engineering, Hunan Institute of Engineering, Xiangtan 411101, China;2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

In order to obtain the changing pattern of contact force of involute gear meshing, a computation method based on dynamic simulation was proposed. The dynamic model of involute gear meshing was established and the computation method for contact force of gear meshing based on Hertz theory was also introduced. With the dynamic model, the contact force and the frequency spectrum of gear meshing,xdirection andydirection were simulated. The simulation results show that the amplitude of the contact force of gear meshing changes obviously. From the moment of meshing approach and meshing recess, the experience of contact force is from 0 kN to maximum and from maximum to 0 kN.Frequency multiplication of 1 and 2 of meshing frequency are in the frequency spectrum of contact force. The contact force of gear meshing ofxdirection andydirection changes obviously with explicit frequency modulation, and the frequency of rotation and frequency of meshing are in the frequency spectrum. The carrier wave is the meshing frequency of gear and the modulation wave is the rotary frequency of gear. The contact force of gear meshing ofxdirection andydirection has the same frequency spectrum and phase difference of 90°.

contact force; gear meshing; simulation

TH132.41；TP391.9

A

1672−7207(2011)02−0379−05

2009−12−07；

2010−03−05

国家自然科学基金资助项目(50804054)；湖南省自然科学基金资助项目(08JJ4011)

黄中华(1979−)，男，湖南娄底人，博士，副教授，从事机电一体化研究；电话：15616273368；E-mail：csu707@163.com