超固结土模型平面应变分叉理论解与数值模拟
2011-01-31孙德安甄文战
孙德安, 段 博, 甄文战
(上海大学土木工程系,上海200072)
土体应变局部化最常见的现象就是岩土工程中宏观剪切带的出现.实际工程中,基坑坍塌、山体滑坡、地基失稳破坏等具有共同的破坏机理,即土体在特定的外荷载作用下产生局部变形,伴随着应变局部化的发展逐渐形成剪切带,最后导致失稳破坏.因此,研究土体应变局部化的形成和发展对评价和预防各类工程事故具有重要意义.
岩土材料应变局部化触发剪切带的现象早已在室内试验中观察到.例如,文献[1-3]通过真三轴试验,分析了应力状态对砂土变形局部化的影响,研究了砂在不同应力路径下的分叉特性;Khalid等[4]对黏性土局部化分叉进行了平面应变及轴对称条件下的试验研究.另外,从理论上对材料局部化分叉加以分析也越来越受到重视.Rudnicki等[5]和Vardoulakis等[6]针对不同性质岩土材料提出了应变局部化准则;Anand等[7-8]应用分叉理论研究了平面应变条件下弹塑性材料的初始剪切带行为;钱建固等[9]理论推导了平面应变条件下Mohr-Coulomb弹塑性模型局部化分叉的理论解.随着计算机计算能力的迅速发展,数值模拟为岩土材料应变局部化研究提供了一个有利途径,其中Huang等[10]采用亚塑性本构模型研究了砂的剪切带问题;徐连民等[11-12]采用高精度欧拉向后应力积分算法,模拟分析了平面应变时正常固结土和超固结土剪切带的形成过程.
本工作主要针对基于伏斯列夫(Hvorslev)面超固结黏土三维弹塑性本构模型[13-14],推导平面应变条件下局部化分叉理论解,并据此理论解给出常平均主应力和常最小主应力平面应变条件下黏土局部化分叉的理论预测;然后,采用与文献[15]相似的方法,编写材料子程序,把基于伏斯列夫面的超固结黏土三维本构模型嵌入到大型非线性有限元软件ABAQUS中,并在平面应变路径下对局部化分叉问题进行数值分析、计算,给出分叉点的数值解;最后,对比分析分叉点的数值解和理论解,验证理论推导的可靠性.
1 超固结黏土本构模型
本构模型的弹塑性矩阵在很大程度上决定了应变局部化的形成与发展.由于复杂的生成条件和地质历史作用,超固结土体受到的前期固结压力大于当前的固结压力时,其力学特性不同于正常固结土,主要表现为低孔隙率、强度高、压缩性小、具有剪胀和应变软化等变形特性.因此,合理选择既能反映应变局部化的变形特点,又能反映土体在数值模拟中的渐进性破坏的超固结土本构模型,显得尤为重要.
本工作采用姚仰平等[13-14]提出的基于伏斯列夫面的超固结黏土三维弹塑性本构模型,该模型可以反映土体硬化、软化、剪缩及剪胀等变形特性.通过变换应力的方法[16]将SMP(spatially mobilized plane)准则与该模型相结合,实现该模型的三维化,从而可以合理地反映土体在三维应力下的变形和强度特性,并且三维化后模型的塑性流动方向与屈服面不正交,为非相关联本构模型.模型的屈服函数表达式为
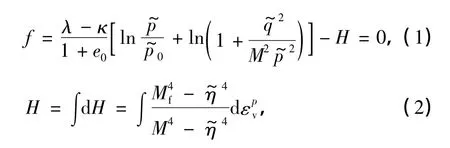
式中,
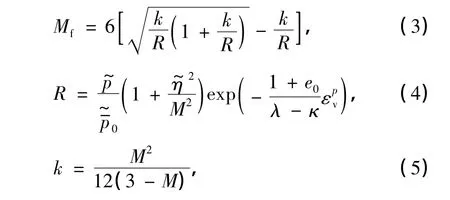
H为硬化参数,λ为压缩指数,κ为回弹指数,e0为初始孔隙比,为塑性体积应变,M为临界状态时的应力比,Mf为潜在强度,为变换应力空间中对应的应力比,及分别为变换应力空间中对应的初始平均应力、平均应力及广义剪应力,为变换应力空间中对应的前期固结压力,R为超固结参数.
2 平面应变局部化分叉解析
应变局部化现象是材料失稳破坏的先兆,它的发生点对应于材料的局部化分叉点,而分叉点的预测又强烈依赖于本构模型的弹塑性矩阵.基于伏斯列夫面的超固结黏土三维本构模型能够合理描述黏土材料应力应变关系、硬化、软化、剪缩及剪胀等变形特性,并且能够合理预测应变局部化的发生.以下就该模型采用Rudnicki等[5]提出的声学张量法对平面应变条件下的局部化分叉进行解析(见图1).

图1 剪切带示意图Fig.1 Chart of shear bands
声学张量法认为:均质各向同性的材料,在应变局部化平面P上的速度场保持连续,而速度梯度场产生跳跃,且速度及速度梯度方向在P面内保持均匀.因此,有
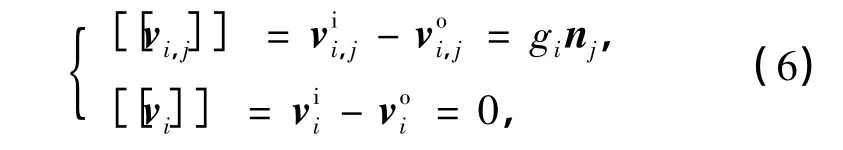
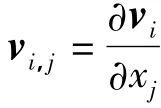
由
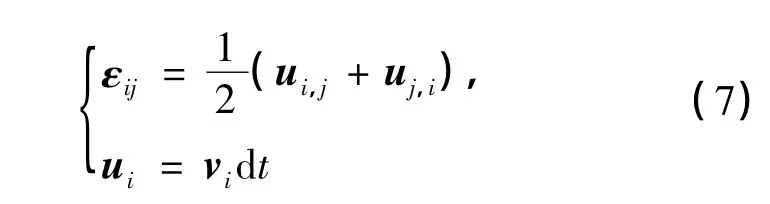
可知
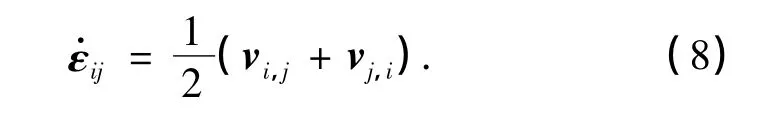
因速度梯度场产生跳跃,则有

式中,εi,j和ε·i,j分别为应变张量和应变率张量,ui为位移张量.
剪切带边界上还满足静力平衡边界条件,即

把式(9)代入式(10),得
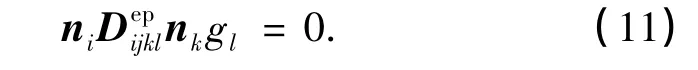
若应变局部化发生,则分叉条件表示为

对于平面应变问题,有

则分叉的表达式为
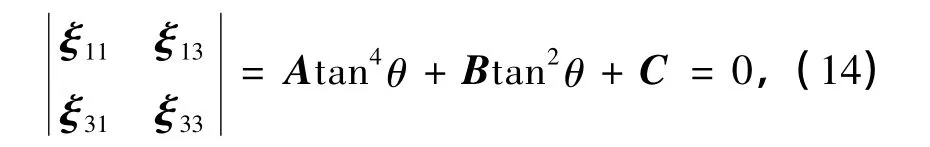
式中,

若材料发生平面应变局部化分叉,则式(14)有实数解.由根的判别式,可知
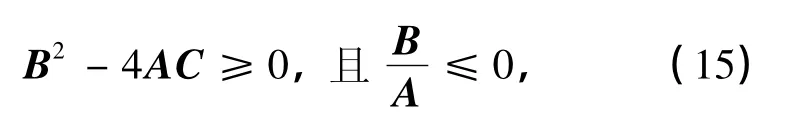
剪切带法线倾角为
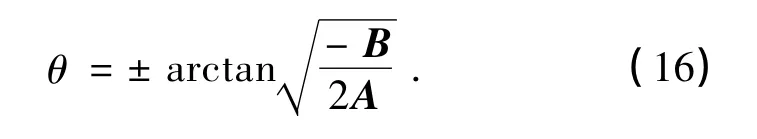
本工作采用的基于伏斯列夫面的超固结黏土三维本构模型的弹塑性矩阵为

式中,
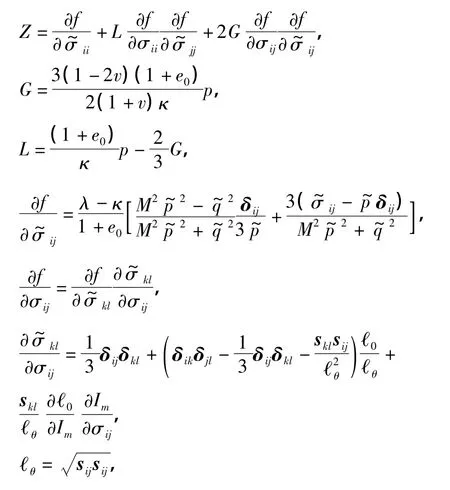

其中p为平均主应力,δij为Kronecker张量,ν为泊松比,I1,I2及I3为第一、第二和第三应力不变量,skl为偏应力张量.
用式(17)中的弹塑性矩阵Dijkl替换式(12)中的,得到的式(15)和(16)即为基于伏斯列夫面的超固结黏土三维本构模型开始触发平面应变分叉的必要条件和相应剪切带法线倾角表达式.
基于本工作中推导的关于基于伏斯列夫面的超固结黏土三维本构模型在平面应变条件下的局部化分叉理论解,下面给出藤森黏土[13-14]局部化分叉的理论预测.藤森黏土的材料特性参数如表1所示.

表1 藤森黏土的模型参数Table 1 Model parameters for Fujinomori clay
根据表1的参数值,可以预测常最小主应力条件下不同超固结比(over-consolidation ratio,OCR)时的应力应变关系和相应的应力比峰值时的应变.图2给出了最小主应力为200 kPa时平面应变条件下不同超固结比藤森黏土的理论解分叉点和峰值点,其中纵坐标对应最大主应变.可以看出,不同超固结比土体的局部化分叉均发生在应力应变塑性硬化阶段,即各分叉点皆在对应的峰值点之前;并且超固结比越大,分叉点越接近峰值点.
图3从理论上分析了最小主应力为200 kPa时,平面应变条件下不同超固结比对剪切带倾角α的影响,α=90°-θ,其中θ为剪切带法线倾角(见图1).由图3可知,当OCR为2时,剪切带倾角α=47.70°,当OCR为12时,θ=51.51°;随着OCR值增大,局部化分叉触发的剪切带倾角呈现缓慢增大的趋势.
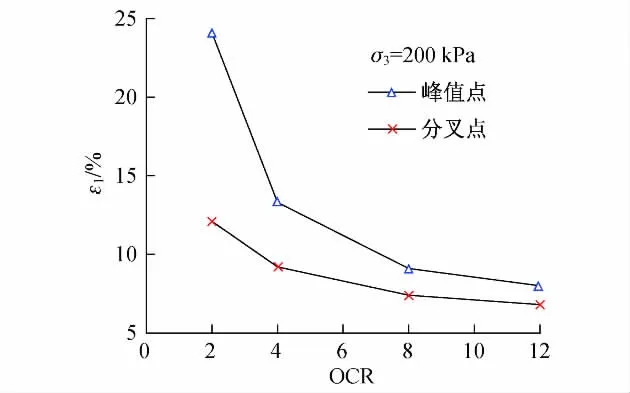
图2 平面应变下不同超固结比的藤森黏土的分叉理论解Fig.2 Analytical solutions for bifurcation of Fujinomori clay with different OCRs under plane strain condition
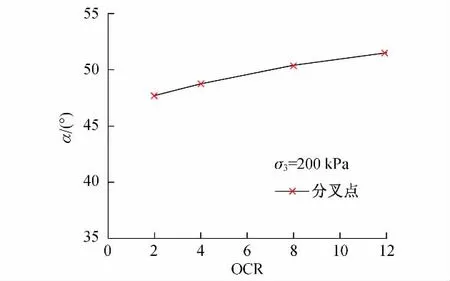
图3 不同超固结比的藤森黏土的剪切带倾角Fig.3 Inclination angles of shear band on Fujinomori clay with different OCRs
图4为理论预测的平均主应力为200 kPa时,平面应变条件下剪切带倾角α随最大主应变ε1变化的过程.当ε1=0~0.9%时,局部化不明显,没能形成剪切带;在ε1=0.9%~2.5%时,开始形成明显的应变局部化平面,且其倾角从产生就开始随着最大主应变的增加而显著减小;局部化继续发展,应变局部化平面倾角趋于稳定,直至ε1=2.9%时,发生分叉,应变局部化平面转变为明显的剪切带.可以看出,分叉发生后,剪切带倾角α减小很缓慢,趋于稳定.
3 平面应变分叉数值预测
3.1 数值解析条件
为验证本工作推导的局部化分叉理论解的可靠性,采用与文献[15]相似的方法编写材料子程序,把基于伏斯列夫面的超固结黏土三维本构模型嵌入到大型非线性有限元软件ABAQUS中,并对超固结黏土在平面应变条件下的局部化分叉问题进行数值预测分析.在计算过程中,因整体刚度矩阵出现奇异,即负特征值,导致计算停止.负特征值表示在应力应变关系曲线的硬化阶段出现负斜率,与原应力应变关系不同,控制偏微分方程由椭圆型变为双曲线型,即分叉.从数学上分析,负特征值意味着刚度矩阵不正定,方程组存在多组解,从而可求得负特征值出现时对应的应力所在位置,即为数值计算的分叉点.

图4 最大主应变与剪切带倾角的关系Fig.4 Relationship between maximum principal strain and inclination angle of shear band
材料的失稳分叉分为弥散连续分叉和不连续失稳分叉,前者指失稳不是以出现明显的不连续带为标志,而是由大量弥散分布的微破坏构成导致的.研究认为,这种分叉对应于材料控制方程椭圆性的丧失,即切线刚度矩阵出现奇异,det(Dep)=0.本工作中数值分析时涉及的分叉就属于弥散连续分叉.不连续分叉指宏观上发生分叉,即出现不连续剪切带,在剪切带上应变场产生跳跃,即det(nDepn)=0.本工作在理论上给出了不连续分叉的解.不连续分叉在弥散连续分叉的基础上考虑了剪切带方向的影响,二者结果相差不会很大.如果本构模型为关联,则弥散连续分叉解对应的硬化模量大于或等于不连续分叉解对应的硬化模量,则不连续分叉先于弥散连续分叉出现;而对非关联模型,弥散连续分叉解对应的硬化模量可能大于、小于或等于不连续分叉解对应的硬化模量,则弥散连续分叉有可能先于或落后于不连续分叉的出现.
因为应变局部化是材料随着均匀加载由均匀变形场过渡到非均匀变形场的一个现象,所以初始均匀各向同性材料就成为本工作数值研究的对象.这里,分析对象为边长10 cm的均匀各向同性立方体,采用8节点六面体线性完全积分单元类型,将试样划分为2 744个单元,有限元网格划分如图5所示.坐标轴x方向设为最大主应力方向,在x方向上,设定试样上下两端面光滑,给上端面施加竖向强制位移;剪切过程中固定住y方向上两端面在y方向上的位移,同时固定下端面在x方向;z方向为应力边界.试样假定为藤森黏土,本构模型参数如表1所示.
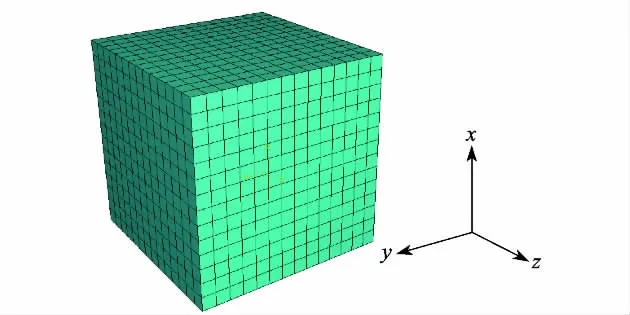
图5 有限元网格Fig.5 Meshes for finite element analysis
3.2 结果分析
图6为数值模拟平面应变条件下的2条不同的应力路径,分别为常最小主应力(σ3=200 kPa)和常平均主应力(p=200 kPa).
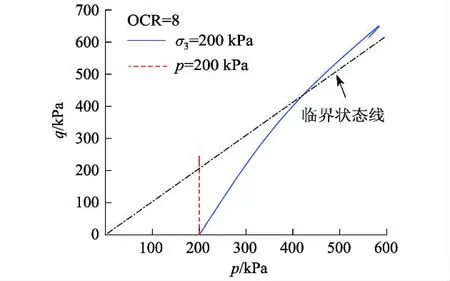
图6 应力路径Fig.6 Stress path
图7为2条不同应力路径的应力应变关系,σ1/σ3为最大主应力与最小主应力之比.图中对比了理论解分叉点与数值解分叉点.当σ3=200 kPa时,理论解分叉点对应最大主应变为7.4%,峰值点对应的最大主应变为9.1%,数值解分叉点对应的最大主应变为5.9%;当p=200 kPa时,峰值点对应的最大主应变为3.6%,理论解分叉点对应的最大主应变为2.9%,数值解分叉点对应的最大主应变为2.7%.上述结果表明,基于伏斯列夫面的超固结黏土三维弹塑性本构模型,在常最小主应力和常平均主应力的剪切应力路径下,应变局部化分叉均发生在土体的应变硬化阶段.
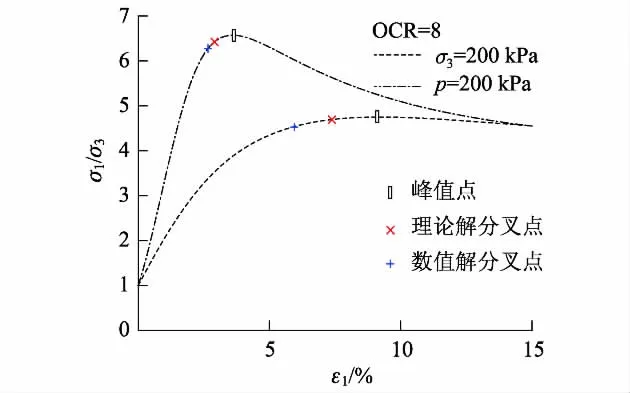
图7 主应变和应力比的关系Fig.7 Relationship between principal strain and stress ratio
图8给出了在σ3=200 kPa时,平面应变条件下不同超固结比的藤森黏土应变局部化分叉理论解与数值解的比较.可以发现,各超固结比下土体的数值解分叉点均发生在峰值前,进一步证实了平面应变条件下土体应变局部化发生在应力应变塑性硬化阶段的理论解结果(见图2);并且随着超固结比的增大,土体强度越高,数值解分叉点越接近峰值点,这与理论解分叉点随固结比的增长而接近峰值点的特点吻合得很好.不同应力路径与超固结比条件下分叉的理论解与数值解的应力比误差如表2所示,不难看出,二者应力比相差较小,这说明了平面应变局部化分叉理论解的合理性.
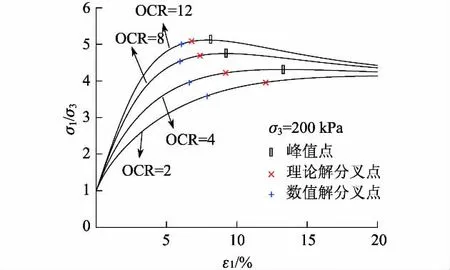
图8 不同超固结比的藤森黏土的应力比应变关系Fig.8 Stress ratio-strain relationships of Fujinomori clay with different OCRs

表2 局部化分叉理论解和数值解应力比的比较Table 2 Comparison of stress ratio between analytical and numerical solutions for localization bifurcation
4 结束语
本工作基于声学张量法系统地对基于伏斯列夫面的超固结黏土三维弹塑性本构模型在平面应变条件下局部化分叉进行了解析,并运用理论解对常最小主应力平面应变条件下不同超固结比土体的分叉点和剪切带倾角进行了对比分析.理论分析表明,超固结比越大,分叉点发生得越早,对应的最大主应变越小,剪切带倾角越大;同时理论分析了常平均主应力平面应变条件下局部化分叉形成的剪切带的倾角随最大主应变变化的关系,理论证明了剪切带形成后,剪切带倾角随最大主应变增大变化微小,趋于稳定;最后,本工作借助非线性有限元软件ABAQUS分别在常最小主应力和常平均主应力平面应变条件下对局部化分叉进行了数值模拟分析,得出了分叉点数值解与理论解基本一致的结论,从而验证了平面应变条件下局部化分叉理论解的可靠性.
[1] CHUJ,LOS C R,LEEI K.Strain softening and shear band formation ofsand in multi-axialtest[J].Geotechnique,1996,46(1):63-82.
[2] WANGQ,LADEP V.Shear banding in true triaxial tests and its effect on failure in sand[J].Journal of Engineering Mechanics,2001,127(8):754-761.
[3] SUND A,HUANGW X,YAOY P.An experimental study of failure and softening in sand under threedimensional stress condition[J].Granular Matter,2008,10(3):187-195.
[4] KHALIDA,ALSHIBLII S A.Strain localization in clay:plane strain versus triaxial loading conditions[J].Geotechnical and Geological Engineering,2007,25:45-55.
[5] RUDNICKIJ W,RICEJ R.Conditions for the localization of the deformation in pressure sensitive dilatant materials[J].Journal of the Mechanics and Physics of Solids,1975,23:371-394.
[6] VARDOULAKISI,SULEMJ.Bifurcation analysis in geomechanics[M].New York:Blackie Academic&Professional,1995.
[7] ANANDL,SPITZIGW A.Initiation of localized shear bands in plane-strain[J].Journal of the Mechanics and Physics of Solids,1980,28(2):113-128.
[8] ANANDL,SPITZIGW A.Shear-band orientations in plane-strain[J].Acta Metallurgica,1982,30(2):553-561.
[9] 钱建固,黄茂松.土体应变局部化现象的理论解析[J].岩土力学,2005,26(3):432-436.
[10] HUANGW X,SUND A,SLOANS W.Analysis of the failure mode and softening behaviour of sands in true triaxial tests[J].International Journal of Solids and Structures,2007,44:1423-1437.
[11] 徐连民,王兴然.用有限变形理论研究黏性土试样中变形的局部化问题[J].岩土工程学报,2004,26(2):125-129.
[12] 徐连民,朱合华,中井照夫,等.超固结粘土的剪切带数值模拟[J].岩土力学,2006,27(1):61-66.
[13] 姚仰平,侯伟,周安楠.基于Hvorslev面的超固结黏土本构模型[J].中国科学:E辑(技术科学),2007,37 (11):1417-1429.
[14] YAOY P,LIZ Q,HOUW,et al.Overconsolidated clay model based on revised Hvorslev envelope[C]∥Proceeding of the 3rd Sino-Japan Geotechnical Symposium. Beijing: China Communication Press,2007:698-705.
[15] 孙德安,甄文战.不同应力路径下剪切带的数值模拟[J].岩土力学,2010,31(7):2253-2258.
[16] MATSUOKAH,YAOY P,SUND A.The Cam-clay model revised by the SMP criterion[J].Soils and Foundations,1999,39(1):81-95.
