一种基于多约束的空间聚类方法

刘启亮，邓 敏，石 岩，彭东亮

中南大学地球科学与信息物理学院，湖南长沙410083

1 引 言

空间聚类是当前地理空间数据挖掘与知识发现的一个重要手段［1－2］，旨在将空间数据库中的实体划分为一系列具有一定分布模式的空间簇，使得同一空间簇中的实体具有最大的相似度，不同空间簇中的实体具有最大差别。当前，空间聚类已广泛应用于犯罪热点分析［3］、地震空间分布模式挖掘［4］、制图自动综合［5－6］、遥感影像分类［7］、公共设施选址［8］、地价评估以及时空建模［9－10］等诸多领域。空间聚类可以分为两种形式，一种是完全依据实体间空间位置的接近程度进行聚类；另一种是同时考虑实体间空间位置邻近与专题属性相似。如何适应空间实体位置分布的复杂性是这两种空间聚类问题共同面临的主要问题。近年来国内外学者曾对这一问题分别进行过研究［4，11－14］。通过分析，将空间实体位置分布的复杂性归纳为以下四个方面：① 空间密度分布不均匀问题，一是不同密度的空间簇［12，13］，二是同一簇中密度不同［11，13］；② 空间簇位置关系的复杂性，一是密度相同或不同的空间簇邻接［12，13］，如“颈问题”［15］，二是两个空间簇相互包含或咬合［11，14］；③ 噪声问题，一是背景噪声［4］，二是链式问题［12－13］，又分单链与多链问题；④ 空间簇的形态差异，包括空间簇形状各异［4，11－14］与空间簇的大小差异［15］。此外，为了深入分析和挖掘地学空间数据库中各要素间的关联规则、分布特征及集聚模式等，在空间聚类过程中一方面需要能够顾及空间实体间专题属性的相似性［16－17］；另一方面，还需要尽可能少地涉及输入参数的设置，以及具有较高的运行效率［12，18］。

现有的空间聚类方法大致可以分为：① 划分的方法［19－20］；② 层次的方法［3，21］；③ 基于密度的方法［11，18，22－23］；④ 基于图论的方法［12－13，15］；⑤ 基于模型的方法［24－25］；⑥ 基于格网的方法［26］。划分的方法对于体积相似、密度相似的球形簇聚类效果较好。但是，这类方法的聚类结果严重依赖初始聚类中心的选择，难以发现任意形状的空间簇，而且当空间簇尺寸、密度变化较大时难以获得满意的聚类结果。传统的层次聚类方法只适合发现球形的空间簇。改进的层次空间聚类方法，如CURE使用代表点的策略虽然能够发现较为复杂结构的空间簇［21］，但是其依然无法发现任意形状的空间簇，而且过多的输入参数增加了算法的使用难度；传统的密度聚类方法，如DBSCAN［18］由于采用固定阈值聚类，难以适应空间实体密度的变化。改进的密度方法［11，22－23］虽然能够在一定程度上顾及空间实体密度的分异特性，然而对于空间簇邻近等问题依然难以很好解决。现有基于图论的聚类方法还不够稳健，容易受空间簇邻接与密度变化的影响。基于模型的方法，需要预先假定空间数据的分布模型，这在某些实际应用中难以准确获得。基于格网的方法虽然聚类效率得到提高，但是聚类质量不高，且易遇到基于密度方法同样的问题［23］。现有顾及专题属性的空间聚类方法大致可以分为三类：① 在空间聚类过程中分别考虑空间邻近域专题属性相似，这类方法多是直接在基于密度方法的基础上顾及专题属性的相似性［16，27－28］，与DBSCAN具有类似的缺陷，同时这类方法大多忽视了专题属性空间分布的非均匀性与趋势性，难以保证同一空间簇中的实体专题属性相似；② 将空间属性与专题属性归一化后加权融合构造距离函数，再采用传统聚类方法进行聚类［9，17］，但是这类方法中空间属性与专题属性间权值的确定比较困难；③ 分别从空间属性和专题属性两方面进行聚类［10，29］，这类方法易受其使用的空间属性聚类与专题属性聚类方法局限性的影响。

综上分析可以发现，分别从空间属性与专题属性两个方面进行聚类，可以适应不同用途的空间聚类应用且可操作性更强。实体间的空间邻近关系的定义是空间聚类的核心问题，Delaunay三角网是空间聚类中实体间邻近关系表达的一种有效工具［3，12］，通过施加不同的距离约束去打断一些不一致的长边，进而获得一系列不连续的子图，每一个子图视为一个空间簇。早期的基于Delaunay三角网的空间聚类方法［30］仅依靠从整体上删除较长的边来进行空间聚类操作，受空间实体密度变化与空间簇邻近的影响较大。后来提出一些改进的基于Delaunay三角网的空间聚类方法。例如，Amoeba算法［3］采取层次删除长边的策略虽然可以发现任意形状的空间簇，但是其依然难以解决“链式问题”以及空间簇邻近问题。Autoclust算法［12］采用多步骤删除长边与短边的方法虽然可以处理某些情况下的“链式问题”以及邻接问题，但是其结果并不稳健。Triclust算法［31］采用多个统计量加权融合的策略删除Delaunay三角网中的不一致边，进而实现空间聚类，然而不同统计量的权值确定比较困难。因此，现有基于Delaunay三角网的空间聚类方法仅依靠距离的约束并不能完全满足复杂情况下的聚类操作，尤其是对于“颈问题”、“链式问题”等情况，空间簇之间需要打断的边经常并不是过长或过短的边，故仅采用距离约束并不能打断这些边，从而导致其存在一定局限。此外，这些方法无法顾及空间实体间专题属性的相似性。为此，本文首先发展一种基于Delaunay三角网的自适应的基于空间实体位置约束的聚类方法。通过对Delaunay三角网中的边施加不同层次、不同类型的约束，获得一系列离散的、由三角网的边连接而成的空间簇；进而，在每个簇中构建实体间的空间邻近关系；最后，将专题属性间的相似度视为一种约束，对空间聚类结果进行过滤，进一步顾及实体间专题属性的相似性。

2 基于多约束的空间聚类

本文的空间聚类方法分为两个步骤：① 基于空间实体位置约束的聚类，获得空间实体的空间分布模式及其空间邻近关系；② 进一步考虑实体间专题属性的相似度，获得最终的聚类结果。下面将针对这两个步骤分别阐述。

2.1 基于空间实体位置约束的聚类

采取一种从整体到局部的层次约束策略对Delaunay三角网的边施加距离约束，进而，发展一种方向约束指标，用来提取空间实体间局部的聚集趋势。首先，仿照文献［3］中的层次边长约束策略来定义整体约束条件，具体表达如下。

定义1 整体约束条件：给定包含n个空间实体的空间数据集SDB，DT表示n个空间实体生成的Delaunay三角网。对于任一空间实体p，其直接Delaunay邻近实体表示为NN（p），CGlobal（p）表示与空间实体p连接的所有边的整体约束条件，表示为

式中，Mean（DT）表示三角网的平均边长；SD（DT）表示三角网所有边的标准差；NI（p）表示噪声点指数；Mean（p）表示与空间实体p连接的所有边的平均值；α表示调节系数，默认设为1。

针对任一空间实体p，若与其直接相连接的边的长度大于整体约束条件，则删除该边。图1（b）为经过整体约束条件删减后的结果。可以发现，整体上分异较为明显的空间聚集现象及噪声点已经很好地被区分，起到了整体约束的效果。其中α可以用于调节整体约束条件的严格程度，α越大，则整体约束条件的敏感性较低，较多的长边将会被保留；α越小，整体约束条件越严格，可能分割整体上的聚集现象。据文献［3］，通过试验证明α可以默认地设为1。

图1 空间数据聚类与空间邻近关系建立Fig.1 Spatial data clustering and the construction of spatial proximity relationship

定义2 K阶邻近：给定一个图G，p为G的一个顶点，则任意一个到p的路径小于或等于K的顶点与p之间满足K阶邻近关系；所有与p满足K阶邻近关系的顶点构成了p的K阶邻域。

本文将一个实体的二阶邻域视为一个局部空间实体集，进一步给出局部约束条件。

定义3 局部约束条件：SG＝｛G1，G2，…，Gm｝为SDB中的所有空间实体在整体约束条件下划分得到的m个图，任一空间实体p的二阶邻域表示为NN2（p）。针对包含k个空间实体的图Gi，p表示图Gi中的任一顶点，CLocali（p）表示p的二阶邻域范围内所有边的局部约束条件，表达为

式中，Mean（NN2（p））表示图Gi中，p的二阶邻域内所有边的平均值；SD（pj）为图Gi中，pj的一阶邻域内所有边的标准差；Mean（SDi）表示图Gi中，所有实体的一阶邻域内边长标准差的平均值；β表示调节系数，默认条件下设为1。

针对图Gi中的任一顶点p，若其二阶邻域内的任一边的长度大于局部约束条件，则将其删除。分析式（3）和式（4）可以发现，局部约束条件实际上是传统的“k倍标准差统计准则”的变种，β值超过2时，局部约束条件敏感性降低仅可能打断整体的长边；β值过小（小于1）时，局部约束过于严格，将会产生过多的小簇，因此β一般设为1～2之间，可以默认设为1。图1（c）为经过局部约束条件进行删边后的结果，下部的两个球型簇A、B与簇C之间的局部长边被很好地打断。经过整体与局部约束，Delaunay三角网中的长边可以有效被打断。但是，某些不一致的边仍然存在，如图1（c），A、B两簇之间形成的“颈”。为此，本文发展一种方向约束条件来解决这种“颈问题”与“链式问题”。主要思想可以描述为：空间实体间的相互作用可以借助一种凝聚力的形式来表达，即空间实体间的相互作用与它们之间的空间距离的平方满足反比关系，实体间距离越远，其相互之间的凝聚力作用越小。Delaunay三角网确定的邻接关系可以用来约束实体间凝聚力的作用范围，即一个空间实体只与其直接Delaunay邻近实体间具有凝聚力作用，与其他实体间的凝聚力作用可以忽略，进而空间实体间的凝聚力作用可以仿照万有引力的形式表达为

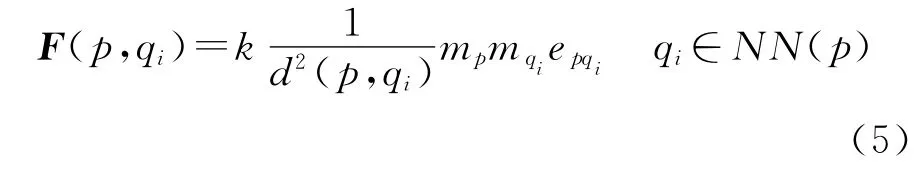
式中，k为凝聚力常数，本文设为1；mp、mqi为实体p、qi的质量，考虑到可以将空间点实体均视为单位质点，故令mp、mqi均为1；d（p，qi）为实体p与qi的欧氏距离；epqi为p指向qi的单位矢量。

进而，针对任一空间实体p，其直接Delaunay邻近域内其他实体对p的凝聚力合力可以表达为

因此，三角网的每条边可以抽象为一条力的作用线，每个空间实体受到的合力方向反映其自然的聚集趋势，故方向约束条件可以进行如下定义。

定义4 方向约束条件：针对任一空间实体p，qi∈NN（p），若qi与p通过公共边连接，则必须满足

式中，CDirection（p）表示实体p与其直接Delaunay邻近实体间的方向约束条件；θ（FT（p）、F（p，qi））表示凝聚合力与凝聚分力的矢量夹角。

方向约束主要是基于物理学中力的合成与分解原理来建立的。若分力与合力的夹角方向小于90°，则说明该分力对合力方向有贡献，空间实体在合力的作用下将具有趋向力源（即产生这些分力的实体）聚集的趋势；若分力与合力的夹角方向大于90°，则该分力对合力方向有削弱作用，空间实体将有背离产生这些分力的实体的趋势。据此可以对一些较为复杂的“颈”或“链”问题进行区分，下面通过一个实例来说明方向约束的应用。

图2（a）为图1（a）中虚线框部分的放大显示，是一种典型的“颈问题”。选取图2（a）中虚线框中部分实体进行分析，图2（b）为其放大显示的情况，A、B两个空间簇被短边p1p2、p1p3形成的“颈”连接起来，从而无法分离。FT（p1）、FT（p2）、FT（p3）分别为实体p1、p2、p3所受的凝聚合力方向（合力的作用线只表示方向不表示标量的大小）。以空间实体p1为例，p1在合力FT（p1）的作用下有向实体q1、q2、q3聚集的局部趋势，同理p3将向q5、q6、q7聚集，p2则趋向于p3、q4、q5，依据方向约束条件p1、p2、p3之间构成的“颈”可以进行自然地区分。这种策略同样也适用于“链式问题”的解决。如图1（d）所示，A、B两个簇经过方向约束条件后，很好地进行了区分。

图2 方向约束简例Fig.2 Example of directional constraint

经过以上三个步骤后，所有通过公共边连接的空间实体即构成一个簇，如图1（d）所示。在此基础上，可以借助Delaunay三角网来构建实体间的邻近关系。具体方法为：在各个簇中依据整体约束条件删边后的实体间的连接关系，采用放宽的局部约束条件删除各个簇边界处的长边，具有公共边的空间实体被定义为互相邻近。由于在聚类过程中，局部约束条件较为严格，在各个簇内部可能打断了部分整体上并不显著的局部长边，如图1（c）所示。因此，在构建实体间邻近关系时，通过增大β值，放宽了局部约束条件。如前文所述，当β值设为2～3时，局部约束条件仅可能打断整体的长边，可以有效避免边界长边的干扰，如图1（e）所示，其中在构建实体间空间关系时均将β设为2。

2.2 基于空间实体位置和专题属性约束的空间聚类

基于空间实体位置约束的空间聚类过程能够获得：① 实体的空间分布模式；② 实体间的空间邻近关系。进一步，需要在每个空间簇中考虑邻近实体间专题属性的约束。通常空间实体的专题属性在空间上的分布是非均匀的，且经常带有某种趋势性，如我国的气温分布从南到北有比较明显的渐变趋势，这些特点在聚类中必须予以充分的考虑。为此，下面引入直接专题属性距离可达与间接专题属性距离相连的概念。

定义5 直接专题属性距离可达：对于空间实体p1、p2，若二者之间具有公共边，且dAttr（p1，p2）≤εdirect，则称p1、p2专题属性距离可达，记为p1↔p2。其中，dAttr（p1，p2）表示实体p1、p2间的专题属性差异，为各维专题属性分别归一化后的欧式距离，具体操作与文献［17］中的方法相同；εdirect表示专题属性差异最小阈值。

定义6 间接专题属性距离相连：对于空间实体集合S＝｛p1，p2，p3，…，pi－1｝，若dAttr（Avg（p1，p2，…，pi－1），pi）≤εindirect，则称S、pi间接专题属性距离相连，记为S⊕pi。其中，Avg（p1，p2，…，pi－1）表示实体p1，p2，…，pi－1的专题属性平均值；εindirect表示间接专题属性距离最小阈值。

顾及专题属性聚类时，选取任一空间实体pi，采用邻域扩张的策略，依次将1阶、2阶、…、K阶邻近域内所有同时满足与pi直接专题属性距离可达与间接专题属性距离相连的实体归为一类，不能归入任何簇的空间实体被标识为异常点，直到所有空间实体或被归入某个空间簇或被标识为异常点时，聚类终止。其中阈值参数εdirect和εindirect的设置类似于文献［16］，即设为最邻近实体专题属性差异的平均值。可见，专题属性聚类过程中既顾及了直接空间邻近实体间的专题属性差异又加入了与整体差异的约束，故能够有效避免专题属性在空间上的渐变造成的影响。

3 试验分析

为了验证本文方法的有效性与优越性，共设计了两组试验。试验1采用如图3（a）所示在Arcgis 9.2中生成的模拟数据库，其中包括了常见的“点云”等不均匀的空间簇；试验2采用两组实际数据，一组是我国西南地区的地震空间分布数据，另一组为我国陆地区域49年年平均气温监测数据。所有试验中，本文方法的各个调节系数均为默认值，即α＝1，施加局部约束时β＝1，构建空间邻近关系时β＝2。

3.1 模拟试验

本文方法针对模拟数据库的聚类结果如图3（b）所示，图3（c）～图3（f）分别给出了K－means、Amoeba、DBSCAN以及Autoclust四种算法的聚类结果。可以发现本文方法的两个重要特点：① 可以有效适应空间实体密度不均匀情况下的空间聚类操作，针对点云的情况（簇9和 10）虽然在边缘处产生个别小簇，但空间簇的主体结构仍可以有效识别；② 可以有效发现空间上邻近的空间簇，如簇1、簇2、簇3。而其他经典方法：①K－means算法对复杂形状的空间簇聚类结果较差，如图3（c），簇3被错误划分为3个簇；②Amoeba算法受“链式问题”与空间簇邻接问题的影响较大，如图3（d），由于“链”和“颈”的影响，簇1、簇2、簇3无法分离，空间簇中实体的分布存在一定差异时，Amoeba算法容易将其错误分割，如图3（d），簇4和簇5的情况；③当空间实体密度差异较大时，DBSCAN算法聚类效果较差，如图3（e），簇6、簇7、簇8被错误归为一类，DBSCAN算法同样受“链式问题”与空间簇邻接问题的影响较大，如图3（e），簇1、簇2、簇3无法区分；④Autoclust算法仅依靠距离约束的策略受“短链”和“颈问题”影响较大，如图3（f），簇1与簇3间的“短链”无法移除，簇1和簇2无法正确区分，同时Autoclust算法可能对一些分布不均匀的空间簇进行错误分割，如图3（f），簇5被错误分成两部分。本文方法比传统方法更具优势的主要原因在于，其顾及了地理现象由整体到局部的层次关系，采取针对性的约束条件进行聚类，而传统方法如K－means与DBSCAN实际上是基于全局参数的，忽视了局部的差异性［3］；Amoeba与Autoclust将整体与局部影响进行融合的策略，缺乏层次性与针对性，导致算法的不稳健。

图3 模拟数据库聚类结果（×——孤立点）Fig.3 Spatial clustering results of simulated datasets（×—outlier）

3.2 实际算例

下面分别采用本文方法进行地震数据空间分布模式挖掘与我国陆地区域气温分布模式挖掘。图4（a）显示了根据文献［32］整理后的我国西南地区（92°E～104°E，21°N～38°N）1970—2004年的134次5级以上强震的空间分布。空间聚类的具体步骤如图4（b）～（d）所示，空间聚类的结果如图4（e）所示，从图中可以比较明显地发现A、B、C、D、E等五条线性地震带，与该地区大的活跃断层构造十分吻合，如A簇主要位于祁连山断层，D簇主要位于丽江—小金河断裂带上，E簇主要位于小江断裂带［32－33］；同时可以发现Ⅰ、Ⅱ、Ⅲ等三个地震丛簇结构，主要位于川滇菱形块体区域［32］，反映了不同方向的断层构造相互作用的结果。聚类结果与文献［32］中的研究结论非常吻合，充分证明了所提出的空间聚类方法在挖掘地震数据空间分布模式中的有效性，可以进一步用于识别该区域的活动断层构造。

图4 地震数据空间分布模式挖掘（×——孤立点）Fig.4 Discovery of spatial patterns in seismic database（×—outlier）

进而，顾及空间实体的专题属性挖掘我国陆地区域49年（1960—2008）年平均气温的空间分布模式。采用国家气象局提供的我国187个气象站的气温监测数据，每个站点的主要属性包括：站点经纬度坐标，高程，年平均气温，建站时间与站点名。同时与一种基于双重距离的空间聚类算法DDBSC进行比较。图5（a）～（d）显示本文方法聚类的具体过程，聚类最终结果如图5（d）所示。这里εdirect、εindirect均设为气象站气温最邻近差异的平均值［16］。分析聚类结果可以发现，图5（d）中由南到北分布的1～8等8个主要空间簇中其平均气温（单位：摄氏度）分别为：24.5、21.7、16.9、10.5、8.8、5.4、3.3、－0.4，较为准确地反应了我国气温由南到北逐渐降低的实际情况，与现有的研究结论相符。DDBSC算法的聚类结果如图5（e）所示，可以发现DDBSC算法从南到北识别了一个条形的空间簇A，显然与实际情况不符。这主要由于我国气温分布由南到北具有渐变性，邻近站点间的差异不大，然而这种差异的积累导致同一空间簇中实体间专题属性的差异性较大。由此亦可说明，本文提出的间接专题属性可达与K阶邻域扩张聚类策略的必要性与实用性。进一步，可以应用本文的聚类结果研究局部地区气温的突变性与差异性，对研究我国气候演变规律具有重要意义。

图5 气温数据空间分布模式挖掘（×——孤立点）Fig.5 Discovery of spatial patterns in temperature database（×—outlier）

4 结论与展望

提出一种基于多约束的空间聚类新方法，通过施加不同层次、不同类型的约束可以适应复杂情况的空间聚类分析。通过模拟试验与实际算例分析可以发现：① 本文方法可以适应空间数据分布不均匀、空间簇形态各异、位置邻近等复杂情况下的聚类，同时对各种噪声影响较为稳健；② 聚类输入参数较少，有利于用户实际使用；③ 聚类结果可以同时满足空间簇中实体既空间邻近又专题属性相似的要求。

进一步的研究工作主要集中在：① 研究空间聚类结果的定量评价方法。目前尚没有一种有效的评价指标能够准确地对空间聚类结果进行定量评价［34］，因此本文对聚类结果的评价主要依赖已有研究论断与先验知识；② 研究专题属性参数的自动确定方法，采用文献［16］中的设置方法实际上是一种全局的策略，在专题属性空间分布不均匀的情况可能存在一定误差，需要进一步顾及专题属性分布的局部特征。

［1］ MILLER H，HAN J.Geographic Data Mining and Knowledge Discovery［M］.2nd ed.London：CRC Press，2009.

［2］ LI Deren，WANG Shuliang，LI Deyi，et al.Theories and Technologies of Spatial Data Mining and Knowledge Discovery［J］.Geomatics and Information Science of Wuhan University，2002，27（3）：221－233.（李德仁，王树良，李德毅，等.论空间数据挖掘和知识发现的理论和方法［J］.武汉大学学报：信息科学版，2002，27（3）：221－233.）

［3］ ESTIVILL－CASTRO V，LEE I.Multi－level Clustering and Its Visualization for Exploratory Spatial Analysis［J］.GeoInformatica，2002，6（2）：123－152.

［4］ PEI T，ZHU A X，ZHOU C H，et al.A New Approach to the Nearest－neighbor Method to Discover Cluster Features in Overlaid Spatial Point Processes［J］.International Journal of Geographical Information Science，2006，20（2）：153－168.

［5］ WU Fang，QIAN Haizhong，DENG Hongyan，et al.Spatial Information Intelligence Management Aims to Map Automatic Generalization［M］.Beijing：Science Press，2008.（武芳，钱海忠，邓红艳，等.面向地图自动综合的空间信息智能处理［M］.北京：科学出版社，2008.）

［6］ GUO Q S，ZHENG C Y，HU H K.Hierachical Clustering Method of Group of Pionts Based on the Neighborhood Graph［J］.Acta Geodaetica et Cartographica Sinica，2008，37（2）：256－261.（郭庆胜，郑春燕，胡华科.基于邻近图的点群层次聚类方法的研究［J］.测绘学报，2008，37（2）：256－261.）

［7］ LUO Jiacheng，LIANG Yi，ZHOU Chenghu.Scale Space Based Hierarchical Clustering Method and Its Application to Remotely Sensed Data Classification［J］.Acta Geodaetica et Cartographica Sinica，1999，28（4）：319－314.（骆剑承，梁怡，周成虎.基于尺度空间的分层聚类方法及其在遥感影像分类中的应用［J］测绘学报，1999，28（4）：319－314.）

［8］ MAO Zhengyuan，LI Lin.The Measure of Spatial Patterns and Its Applications［M］.Beijing：Science Press，2004.（毛政元，李霖.空间模式的测度及其应用［M］.北京：科学出版社，2004.）

［9］ JIAO Limin，LIU Yaolin，LIU Yanfang.Spatial Autocorrelation Patterns of Datum Land Price of Cities in a Region［J］.Geomatics and Information Science of Wuhan University，2009，34（7）：873－877.（焦利民，刘耀林，刘艳芳.区域城镇基准地价水平的空间自相关格局分析［J］.武汉大学学报：信息科学版，2009，34（7）：873－877.）

［10］ WANG Haiqi，WANG Jinfeng.Local Neural Networks of Space－time Modeling Based on Partitioning for Lattice Data in GIS［J］.Journal of Remote Sensing，2008，12（5）：707－715.（王海起，王劲峰.基于分区的局域神经网络时空建模方法研究［J］.遥感学报，2008，12（5）：707－715.）

［11］ NOSOVSKIY G V，LIU D，SOURINA O.Automatic Clustering and Boundary Detection Algorithm Based on Adaptive Influence Function［J］.Pattern Recognition，2008，41（9）：2757－2776.

［12］ ESTIVILL－CASTRO V，LEE I.Argument Free Clustering for Large Spatial Point－data Sets［J］.Computers，Environment and Urban Systems，2002，26（4）：315－334.

［13］ ZHONG C，MIAO D Q，WANG R Z.A Graph－theoretical Clustering Method Based on Two Rounds of Minimum Spanning Trees［J］.Pattern Recognition，2010，43（3）：752－766.

［14］ HANDL J，KNOELES J.An Evolutionary Approach to Multiobjective Clustering［J］.IEEE Transactions on Evolutionary Computation，2007，11（1）：56－76.

［15］ ZAHN C T.Graph－theoretical Methods for Detecting and Describing Gestalt Clusters［J］.IEEE Transaction on Computers，1971，C20（1）：68－86.

［16］ LI Guangqiang，DENG Min，CHENG Tao，et al.A Dual Distance Based Spatial Clustering Method［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：482－488.（李光强，邓敏，程涛，等.一种基于双重距离的空间聚类方法［J］.测绘学报，2008，37（4）：482－488.）

［17］ LI Xinyun，ZHENG Xinqi，YAN Hongwen.On Spatial Clustering of Combination of Coordinate and Attribute［J］.Geography and Geo－Information Science，2004，20（2）：38－40.（李新运，郑新奇，闫弘文.坐标与属性一体化的空间聚类方法研究［J］.地理与地理信息科学，2004，20（2）：38－40.）

［18］ ESTER M，KRIEGEL H P，SANDER J，et al.A Density－based Algorithm for Discovering Clusters in Large Spatial Databases with Noise［C］∥Proceeding of the 2nd the International Conference on Knowledge Discovery and Data Mining.Portland：AAAI Press，1996：226－231.

［19］ MACQUEEN J.Some Methods for Classification and Analysis of Multivariate Observations［C］∥Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability.Berkeley：University of California Press，1967：281－297.

［20］ NG R T，HAN J.Efficient and Effective Clustering Method for Spatial Data Mining［C］∥Proceedings of the 20th International Conference on Very Large Data Bases.San Francisco：Morgan Kaufmann Publishers Inc，1994：144－155.

［21］ GUHA S，RASTOGI R，SHIM K.CURE：An Efficient Clustering Algorithm for Large Databases［C］∥Proceedings of 1998ACM－SIGMOD International Conference on Management of Data.New York：ACM，1998：73－84.

［22］ LI Guangqiang，DENG Min，LIU Qiliang，et al.A Spatial Clustering Method Adaptive to Local Density Change［J］.Acta Geodaetica et Cartographica Sinica，2009，38（3）：255－263.（李光强，邓敏，刘启亮，等.一种适应局部密度变化的空间聚类方法［J］.测绘学报，2009，38（3）：255－263.）

［23］ PEI T，JASRA A，HAND D J，et al.DECODE：A New Method for Discovering Clusters of Different Densities in Spatial Data［J］.Data Mining and Knowledge Discovery，2009，18（3）：337－369.

［24］ DEMPSTER A，LAIRD N，RUBIN D.Maximum Likelihood from Incomplete Data via the EM Algorithm［J］.Journal of the Royal Statistical Society：Series B，1977，39（1）：1－38.

［25］ XU X W，ESTER M，KRIEGE H P，et al.A Distributionbased Clustering Algorithm for Mining in Large Spatial Databases［C］∥Proceedings of the 14th International Conference on Data Engineering.Washington：IEEE Computer Society，1998，324－331.

［26］ WANG W，YANG J，MUNTZ R.STING：A Statistical Information Grid Approach to Spatial Data Mining［C］∥Proceedings of the 23rd International Conference on Very Large Data Bases.San Francisco：Morgan Kaufmann Publishers Inc，1997：186－195.

［27］ ZHOU J G，GUAN J H，LI P X.DCAD：A Dual Clustering Algorithm for Distributed Spatial Databases［J］.Geo－spatial Information Science，2007，10（2）：137－144.

［28］ BIRANT D，KUT A.ST－DBSCAN：An Algorithm for Clustering Spatial－temporal Data［J］.Data ＆Knowledge Engineering，2007，60（1）：208－221.

［29］ LIN C R，LIU K H，CHEN M S.Dual Clustering：Integrating Data Clustering over Optimization and Constraint Domains［J］.IEEE Transactions on Knowledge and Data Engineering，2005，17（5）：628－637.

［30］ KANG I，KIM T，LI K.A Spatial Data Mining Method by Delaunay Triangulation［C］∥Proceedings of the 5th ACM international workshop on Advances in geographic information systems.New York：ACM，1997：35－39.

［31］ LIU D，NOSOVSKIY G V，SOURINA O.Effective Clustering and Boundary Detection Algorithm Based on Delaunay Triangulation［J］.Pattern Recognition Letters，2008，29（9）：1261－1273.

［32］ JIANG Haikun，LI Yongli，QU Yanjun，et al.Spatial Distribution Features of Sequence Types of Moderate and Strong Earthquakes in Chinese Mainland［J］.Acta Seismologica Sinica，2006，28（4）：389－398.（蒋海昆，李永莉，曲延军，等.中国大陆中强地震序列类型的空间分布特征［J］.地震学报，2006，28（4）：389－398.）

［33］ HUANG Fugang，LI Zhonghua，QIN Jiazheng，et al.Correlation of Seismicity in Sichuan－Yunnan Rhombic Block［J］.Journal of Seismological Research，2007，30（3）：205－209.（皇甫岗，李忠华，秦嘉政，等.川滇菱形块体强震活动关联分析［J］.地震研究，2007，30（3）：205－209.）

［34］ YUE S Y，WANG J S，WU T，et al.A New Separation Measure for Improve the Effectiveness of Validity Indices［J］.Information Sciences，2010，180（5）：748－764.