基于灰色关联分析的平面磨削工艺参数优化
2011-01-29李郝林
李郝林 王 健
上海理工大学,上海,200090
基于灰色关联分析的平面磨削工艺参数优化
李郝林 王 健
上海理工大学,上海,200090
通过分析表面粗糙度和平面度,运用灰色关联分析方法来优化平面磨削中的工艺参数(砂轮转速、进给方式、进给速度、磨削深度、磨削液浓度和磨削时间等)。在实验中,使用正交排列来设计实验,通过计算得到灰色关联度,从而决定最优的工艺参数。实验结果表明,通过该方法可有效地减小平面磨削中的表面粗糙度和平面度。
表面粗糙度;平面度;平面磨削;灰色关联分析;优化
0 引言
在平面磨削尤其是光学玻璃等脆性材料的高精度平面磨削中,平面度和表面粗糙度是衡量磨削质量的重要标准。平面磨削较为复杂,砂轮转速、进给方式、进给速度、磨削深度、磨削液浓度和磨削时间都是影响平面度和表面粗糙度的重要加工工艺参数。为了改进加工质量,提高磨削效率,需要一种有效的方法来选择最优的工艺参数。
按国际惯例,控制论中,信息量多少常以颜色深浅来表示。信息充足、确定(已知)的为白色,信息缺乏、不确定(未知)的为黑色,部分确定与部分不确定的为灰色。灰色系统理论由华中科技大学邓聚龙教授于1982年提出[1],它以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息进行生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。
现有的文献多是对工件材料的工艺参数进行优化。Tay lor[2]最先将最优速度的概念引入金属加工中,而后出现了许多以达到更好经济效益为目的的优化加工参数方法。Bhattacharyaa等[3]用拉格朗日乘子法来寻求最优切削参数;Erm-er[4]使用几何编程法来寻求最优切削参数。王剑彬等[5]以最高生产率为目标函数,运用模糊优化设计方法确定磨削加工中最佳的磨削参数。还有很多研究者根据实际生产现场条件调整影响磨削的因素来安排多因素实验,并建立对生产实践具有指导意义的数学模型,进而优化工艺参数。平面磨削的磨削机理复杂,加工工艺参数的选择主要依靠人的经验,而影响平面磨削质量的因素众多,除了工艺参数外,磨床发热、振动等也会对最后的磨削质量产生较大的影响。在实际加工生产中,很难对机床发热、主轴热变形以及振动等非工艺参数的影响因素进行测量,进而寻找其与加工质量的关系。
本文利用灰色关联度分析方法来优化平面磨削中多个参数因素,在含未知信息的情况下利用灰色理论研究最优工艺参数选择方法。通过灰色关联度分析方法不但可以确定最优工艺参数,还可以确定出对平面磨削影响最大的加工工艺参数因素以及参数因素的排序。实验证明该方法是有效、可行的。
1 实验方案拟定
1.1 光学玻璃
平面磨削实验的工件材料为K 9玻璃,其努氏硬度为5.5级。衡量光学玻璃磨削效果的主要指标有光学玻璃的折射率,在机械加工中,主要是利用光学玻璃的表面粗糙度和平面度来反映折射率的大小。
1.2 超精密平面磨床
实验使用德国斯来福临公司生产的K-PT型精密平面磨床,该磨床不仅保持了平面成形磨床高刚性和高精密的特点,而且其交互式的人机界面和灵活简便的操作面板使得编程和操作工作非常轻松舒适。该磨床的三个进给轴均采用高精度直线滚子导轨和精密预紧循环式滚珠丝杠,配以交流伺服马达进行驱动,Y轴和Z轴标配直线光栅尺,能够实现高精度的成形磨削。其主轴最高转速4500r/min,工件主轴有很高的刚度、回转精度和振动吸收率,磨削深度能控制在0.1μm之内,采用金刚石砂轮磨削工件时调配进口日本磨削油作为冷却液。
1.3 实验工作
在平面磨削K 9玻璃的实验(图1)中,使用金刚石砂轮作为磨具。

图1 平面磨削实验
实验中考虑如下工艺参数:砂轮转速(m/s)、进给方式、进给速度(mm/min)、磨削深度(μm/次)、磨削时间(min)。平面磨削的效果主要考虑以下两方面:①表面粗糙度Ra;②平面度 f。使用日本M itutoyo公司生产的SJ-201表面粗糙度测量仪进行表面粗糙度测量,使用M icro-Epilon公司生产的CapaNCDT6300平面度测量仪进行平面度测量。
实验中各个因素的取值条件如表1所示。
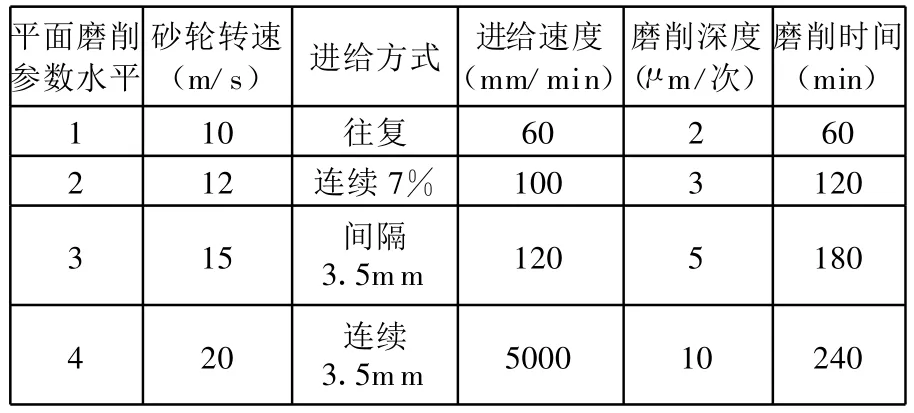
表1 各因素参数表
在平面磨削中,平面磨床的砂轮主轴方向为Y轴方向,砂轮主轴上下移动的方向为Z轴方向,砂轮左右移动方向为X轴方向。进给方式表示沿Y轴方向砂轮的运动方式,进给速度表示沿X轴方向工作台的速度,在平面磨削中,工作台是来回往复运动的。砂轮磨削深度表示沿Z轴方向砂轮每次进给的磨削量。
根据表1,全部实验因素的组合需要45=1024次,这是不现实的。在本实验中,使用Taguchi法来设计正交试验表(采用 Taguchi法设计多特性参数很有效)。根据Taguchi法的正交设计[6-7],实验设计了一个L16的正交序列,如表2所示,实验结果亦总结在表2中。

表2 使用正交序列L16表设计的实验及实验结果
2 灰色关联度分析
在一个灰色系统中,各个因素之间的关系是不确定的[8-9]。在灰色系统理论中,灰色关联度研究就是研究给定系统中一个主要影响因素和其他因素之间的关系。当实验模糊或者实验方法不确定时,灰色分析可以补偿统计回归缺失的信息[10]。灰色关联度研究实际上是测量不同序列数据的绝对值的差异性,进而将序列之间近似的关系显示出来[11]。
2.1 实验数据预处理
在一个数据序列中,由于因素的范围和单位不同,所以需要对数据进行预处理。同时,当数据序列的范围太大,或者数据序列的目的方向不同时,同样需要对数据序列进行预处理。数据预处理就是将原始数据序列转化为对比数据序列。由于数据序列的特点多样,所以在灰色关联度研究中有多种数据预处理方法[12]。
若原始数据序列特性是“越高越好”,则对原始数据序列处理的公式如下:

2.2 灰色关联系数与灰色关联度
在灰色关联度分析中,两个系统或者两个序列之间的关联性就是灰色关联度。数据预处理之后,第k个参数特性在第i次实验中的灰色关联系数ξi(k)为[10-12]

式中,Δoi(k)为参考序列Xo(k)与对比序列(k)的偏差;ψ为偏差系数,ψ∈[0,1],ψ的值根据实际系统来调节,ψ越小,说明偏差越大,通常ψ=0.5。
得到灰色关联系数以后,就要根据其平均值来求灰色关联度[10,12]。灰色关联度计算公式如下:
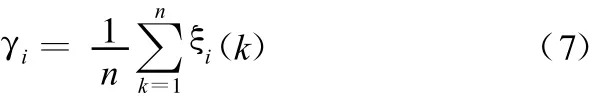
然而,在真实的工程系统中,不同参数因素的重要性是不同的。这时灰色关联度就由式(7)扩展为[10,12-13]

这里,ωk是因素k的标准化度量,如果度量相同,则式(7)、式(8)是相等的。
灰色关联度γi表示参考序列Xo(k)与对比序列(k)的相关程度。如果两个序列是相同的,那么灰色关联度的值为1。灰色关联度还能够反映对比序列对参考序列的影响程度。因此,如果某一对比序列比其他对比序列更能影响参考序列,那么该对比序列的灰色关联度要高于其他对比序列的灰色关联度。
3 实验结果分析
在平面磨削中,表面粗糙度和平面度值都是越小越好,那么对数据进行预处理时,将表2中粗糙度结果和平面度结果代入式(2),分别得到粗糙度的对比序列和平面度的对比序列,如表3所示,即将粗糙度结果Ra作为一个原始序列,平面度结果f作为一个原始序列,代入式(2),分别得到粗糙度和平面度的对比序列。

表3 数据预处理结果
偏差序列按照式(6)计算,如下所示:

因此,Δo1=(0.5273,0.8387),用同样的计算方法将i=1,2,…,16代入式(6),计算得到 Δo i列于表4中。根据表4的结果,Δm in和 Δmax的值为

将偏差系数ψ代入式(5),计算灰色关联系数。如果所有的因素参数重要水平相同,ψ的值即为0.5。在这个L16正交排列的实验中,可以用式(5)和式(8)计算每次实验的灰色关联系数和灰色关联度,如表5所示。

表4 偏差序列

表5 16个对比序列的灰色关联系数和灰色关联度
根据表2的实验设计,可从表5和图2中看出实验11拥有最高的灰色关联度,因此,实验11的加工工艺参数是16次实验中同时具有最小表面粗糙度、最小平面度的最优加工工艺参数,即A 3、B3、C1、D 2和 E4 代表的最优平面磨削工艺参数(砂轮转速为15m/s(水平3)、进给方式为间隔3.5mm(水平3)、进给速度为60mm/min(水平1)、磨削深度为 3μm/次(水平 2)、磨削时间为240m in(水平4))为最优加工工艺参数。
除了可以寻找到获得最好平面磨削加工质量的最优加工工艺参数以外,灰色关联度分析还可以计算磨削工艺参数每一水平的灰色关联度平均值。计算过程如下:①将正交排列中的灰色关联度依照参数水平分组;②计算平均值。例如,因素A(砂轮转速)在水平1时的灰色关联度平均值0 5992。平面磨削每一个参数因素的每一个水平都可以用同样的方法来计算平均灰色关联度,如表6所示。
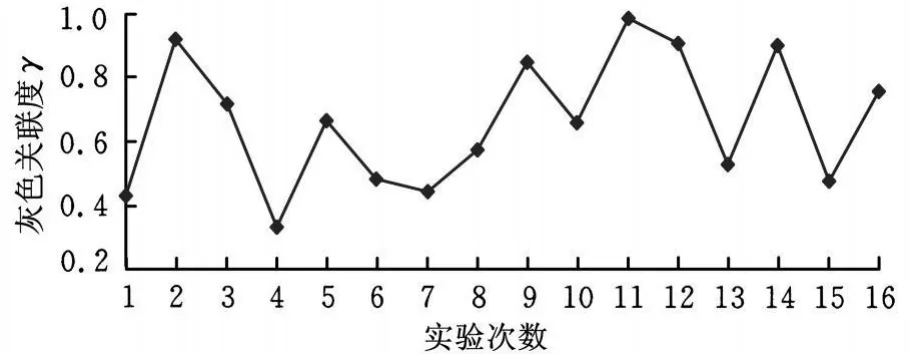
图2 16次实验的灰色关联度

表6 各参数因素各水平平均灰色关联度
表6中的灰色关联度表示参考序列与对比序列各个水平之间的关系,灰色关联度越大表示对比序列与参考序列之间的关联性越大[12]。换言之,不考虑参数种类,关联度越大表示某参数水平的特性越好[13]。因此,具有最大关联度的工艺参数水平即是最优的工艺参数。表 6中,带星号“*”的关联度表示平面磨削效果更好的因素水平的关联度。基于表6,表面粗糙度和平面度的最优加工工艺参数是 A 3、B2、C3、D2和 E2,即砂轮转速15m/s(水平3)、进给方式为连续7%(水平2)、进给速度120mm/m in(水平 3)、磨削深度3μm/次(水平2)、磨削时间120min(水平2)。
图3示出了平面磨削各因素水平特性的灰色关联度,最大的δmax值即为对平面磨削质量影响最大的参数因素。在表 6中,最大的δmax值为0.3099,所以砂轮转速对平面磨削的质量影响最大。同样,可以对各个参数因素对平面磨削质量的影响进行排序,依次是砂轮转速(A)、进给速度(C)、磨削深度(D)、磨削时间(E)、进给方式(B)(0.3099>0.2671>0.2172>0.2082>0.1226)。
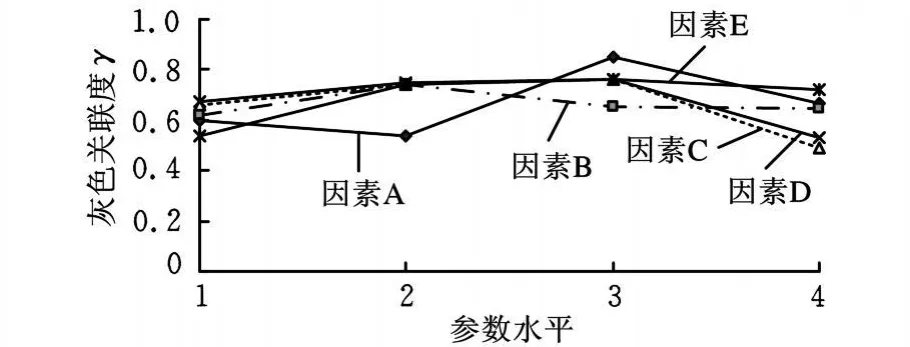
图3 各因素各水平的平均灰色关联度
通过实验设计与分析可以发现,灰色关联分析能够衡量磨削质量与工艺参数之间的关联程度,它可以选取一组使得关联度最大的工艺参数的因素水平组合,同时分析出在哪一种工艺参数与磨削质量之间的关联程度最大,即对磨削质量影响最大。在实际加工中,机床振动、机床发热都会对磨削质量产生一定的影响,如机床发热会使主轴产生一定的热变形,从而影响加工精度。在现代数据分析中,方差分析仅适用于考虑到的因素水平,对于未知的影响因素(如机床振动等),都没有办法详尽合理地去分析;在回归分析中,对于满足基本假设的回归模型,回归分析理论已经成熟,但对于违背基本假设的回归模型的参数估计仍然有很多问题需要解决,而且对未知参数的非线性问题,有多种非线性回归,需要根据实际情况来选择。与方差分析和回归分析相比较,灰色关联分析更适用于研究平面磨削工艺。平面磨削中,未知的影响因素较多,无法一一具体分析,灰色关联分析将所有未知的因素对平面磨削质量的影响都考虑却不进行具体的研究分析,仅仅研究在未知影响因素存在的条件下,哪种工艺参数是最优的。实验证明了灰色关联分析对一个系统发展变化态势提供了量化的度量,非常适合动态过程分析,简单有效。
4 结语
本文在平面磨削过程中,用灰色关联分析的方法对多个特性(粗糙度和平面度)的最优加工工艺参数进行了筛选,得出了灰色关联分析是一种研究平面磨削最优工艺参数的方法。表面粗糙度和平面度是衡量平面磨削质量的两个参数,通过平均灰色关联度分析,找到砂轮转速是对平面磨削质量影响最大的因素。各个参数因素对平面磨削质量的影响顺序为:砂轮转速、进给速度、磨削深度、磨削时间、进给方式。实验结果证明该方法可以有效地改进平面磨削加工质量。
该方法还可以推广到不同的加工工件材料,不仅仅是脆性材料,对于金属等塑性材料同样适用,更进一步,在外圆磨削、车削、钻削中也适用。本文的灰色关联度分析法还可以进一步完善,针对实际的平面条件,考虑更多的加工工艺参数与条件,例如磨削液浓度、光学玻璃的其他表面质量参数等,从而优化更多的加工工艺。
[1] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010.
[2] Tay lor F W.On the A rt o f Cutting Metals[J].T rans.ASM E,1907,28:31-350.
[3] Bhattacharyya A,Faria-Gonzalez R,H am I.Regression Analysis for Predicting Surface Finish and Its Application in the Determination of Optimum Machining Conditions[J].ASME J.England,1970,92(3):711-714.
[4] Ermer D S.Optim ization of the Constrained Machining Econom ics Problem by Geometric Programm ing[J].ASME J.England,1971,93:1067-1072.
[5] 王剑彬,王勤思.磨削加工中磨削参数的模糊优化设计[J].南华大学学报(自然科学版),2005,19(1):29-31.
[6] Ross P J.Taguchi Techniques for Quality Engineering[M].2nd ed.New York:M cG raw-H ill,1996.
[7] Tosun N,Ozler L.Op tim ization for H ot Turning Operations w ith Mu ltip le Performance Characteristics[J].Int.J.Adv.Manuf.Technol.,2004,23(11/12):777-782.
[8] Wang CC L,Chen S F,Yuen M M F.Fuzzy Part Fam ily Formation Based on Grey Relational Analysis[J].Int.J.Adv.Manu f.Techno l.,2001,18:128-132.
[9] Deng J L.Introduction to G rey System Theory[M].J.Grey System,1989,1:1-24.
[10] Lin Z C,H o C Y.Analysis and App lication of G rey Relation and Anova in Chem ical-mechanical Polishing Process Parameter[J].Int.J.Adv.Manu f.Technol.,2003,21(1):10-14.
[11] Fung CP.Manu facturing Process Op tim ization for Wear Property of Fibre-reinforced Polybuty lene Terephtha late Compositesw ith G rey Relational A-nalysis[J].Wear,2003,254:298-306.
[12] Lo S P.The Application of an ANFIS and Grey System Method Inturning Too l-failure Detec tion[J].Int.J.Adv.Manuf.Technol.,2002,19(8):564-572.
[13] Tosun N,Cogun C,Pih tili H.The Effect o f Cutting Parameters onWire CraterSizes in Wire EDM[J].Int.J.Adv.Manuf.Technol.,2003,21(10/11):857-865.
Determ ination ofOptimum Parameters in Plane Grinding by Using Grey Relational Analysis
Li Haolin Wang Jian
University of Shanghai for Science and Techno logy,Shanghai,200090
The grey relational analysisw as used for optimizing the p lane grinding p rocess parameters for the w ork piece surface roughness and the flatness.Various grinding parameters,such as grindingw heel speed,mode of feeding,feeding speed,grinding dep th,grinding concentration and grinding time were considered.An orthogonal array was used for the experimental design.Optimal machining parametersw ere determined by the grey relational grade obtained from the grey relational analysis formulti-perform ance characteristics(the surface roughness and the flatness).Experimental results show that the surface roughness and the flatness in plane grinding process can be im proved effectively through the new approach.
surface roughness;flatness;p lane grinding;grey relationalanalysis;optim ization
TH 162
1004—132X(2011)06—0631—05
2010—03—12
国家重大科技专项(2011ZX 04004-051);上海市科学技术委员会资助项目(08110511600)
(编辑 苏卫国)
李郝林,男,1961年生。上海理工大学机械工程学院院长、教授、博士研究生导师。主要研究方向为数控技术、精密检测与智能控制。获省部级科技进步二等奖、三等奖各1项。获中国发明专利和实用新型专利各 1项。获软件著作权1项。发表论文60余篇。王 健,男,1985年生。上海理工大学机械工程学院硕士研究生。
