甘肃地区三水准超越概率水平地震动峰值加速度关系与场地放大效应研究

滕光亮，陈永明

（1.中国地震局兰州地震研究所，甘肃 兰州 730000；2.中国地震局黄土地震工程开放实验室，甘肃 兰州 730000；3.甘肃省岩土防灾工程技术研究中心，甘肃 兰州 730000)

0 引言

新的建筑抗震设计规范[1]已于 2010年 12月 1日开始实施，其中对于一般建筑的设计基准期仍定为50年，依然采用“三水准设防”的抗震设计思想，即对于多遇地震、基本地震、罕遇地震，通常也将其称之为“小震、中震、大震”，相应的超越概率分别为 50年 63.5%、10%和 2%-3%，重现期分别为50年、475年和1600～2400年。按规范要求，采用“小震”地震动参数计算结构的弹性地震作用标准值和相应的地震作用响应，进行结构构件的截面承载力验算，以期在满足“小震”承载力可靠度的同时满足“中震可修”的目标，“大震”用于有特殊要求的建筑、地震时易于倒塌的结构等的弹塑性变形验算，要求变形不超过容许的限值以防倒塌[1]。

在《地震安全性评价管理条例》中，对重大工程的地震动参数取值要求必须做专门的研究；除此之外的一般工程规定按照地震动峰值加速度区划图取值。而我国现行的地震动参数区划图仅给出 50年超越概率10%的地震动峰值加速度，所以，在按照“三水准设防”原则进行建筑抗震设计时，如何对50年超越概率63%和2%-3%的地震动峰值加速度取值，成为抗震设计工作者非常关心的问题。此外，对工程场地的放大效应即地面与基岩地震动峰值加速度关系的研究，对提高地震安全性评价工作的水平和质量具有积极的意义。

本文研究甘肃省近十年来各类建筑场地的安全性评价中计算得出的不同概率水平下场地水平地震动峰值加速度之间的关系及工程场地条件对峰值加速度的放大效应，为甘肃省工程抗震设计中设计地震动参数的取值提供必要的参考。所选择的158个场地分布如图1所示。

图1 工程场地分布图Fig.1 Distribution map of the studing site in Gansu province.

1 地震动特性

对工程抗震而言，一般认为地震动的特性可以通过三要素来描述：振幅、频谱和持时。所谓振幅，可以指地震动加速度、速度、位移三者之一的峰值、最大值或某种意义上的有效值。凡是表示一次地震动中振幅与频率关系的曲线，统称为频谱，在地震工程中常用傅里叶谱、反应谱以及功率谱。根据实际震害调查资料、结构的低周疲劳现象、破坏的累积效应、实验与理论分析，大多数地震工程学家都认为将地震动持时作为地震动特性的三要素之一具有极为重要的意义[2]。

地震动的工程特性必须包括这三个基本要素[2]。本文仅从振幅着手，探讨不同超越概率水平下PGA之间的关系。

长期以来，工程界普遍比较接受含有最大值或有效峰值含义的定义。虽然各种有效峰值具有明确的物理意义，但由于主观性较强，所得的值离散性也较大。但对于工程抗震而言，仍以采用最简单的最大峰值为主[3]。当人们对加速度过程a(t)本身及其与结构反应的关系进行研究之后，发现由于PGA常常与地震动的高频部分相关，而由高频部分决定的a(t)中的个别峰值对结构反应的影响并不显著，因此，PGA的研究并非是描述地震动特性最理想的参数。另外，除了结构振动产生的破坏以外，也有许多震害是由于地面运动的速度和位移比较显著而造成的。地震动的峰值速度与地震动的能量有关，峰值位移与变形有关[4]，所以用地震动的峰值速度和峰值位移可以作为衡量地震动强弱的标志。

2 三水准概率水平下的地震动峰值加速度关系

在现行的《中国地震动参数区划图》中，将50年设计基准期超越概率 10%的地震加速度的设计取值规定为地震动峰值加速度，即设计基本地震加速度。而根据“三水准设防”标准进行建筑物的抗震设计时，50年超越概率63.5%和2%-3%的地震动峰值加速度如何取值才能达到抗震设防的目的？因此，探讨他们之间的关系便具有重要的现实意义。

2.1 基岩的地震动峰值加速度相对变化

将50年超越概率63.5%和2%-3%基岩地震动峰值加速度分别与50年超越概率10%基岩地震动峰值加速度求比值（表1）。

表1 50年不同超越概率水平下基岩PGA比值

数据表明，50年超越概率63.5%与50年超越概率10%的基岩峰值加速度比值的平均值为0.304，标准差为0.031。50年超越概率2%-3%与50年超越概率10%的基岩峰值加速度比值的平均值为1.867，标准差为0.125。

2.2 场地的地震动峰值加速度值相对变化

按场地类别进行分类，将50年超越概率63.5%和 2%-3%的场地设计地震动峰值加速度分别与 50年超越概率10%的场地设计地震动峰值加速度求比值（表2）。

数据表明，50年超越概率63.5%与50年超越概率10%的场地设计地震动峰值加速度比值，在Ⅰ类场地的平均值为0.339，标准差为0.022；Ⅱ类场地的平均值为0.336，标准差为0.027；Ⅲ类场地的平均值为0.332，标准差为0.018。其平均值随场地条件变差呈现出缓慢减小的趋势。50年超越概率2%-3%与 50年超越概率 10%的场地设计地震动峰值加速度的比值，在Ⅰ类场地的平均值为1.782，标准差为0.084；Ⅱ类场地的平均值为1.839，标准差为 0.121；Ⅲ类场地的平均值为 1.862，标准差为0.090。其平均值随场地条件变差呈现出缓慢增大的趋势。

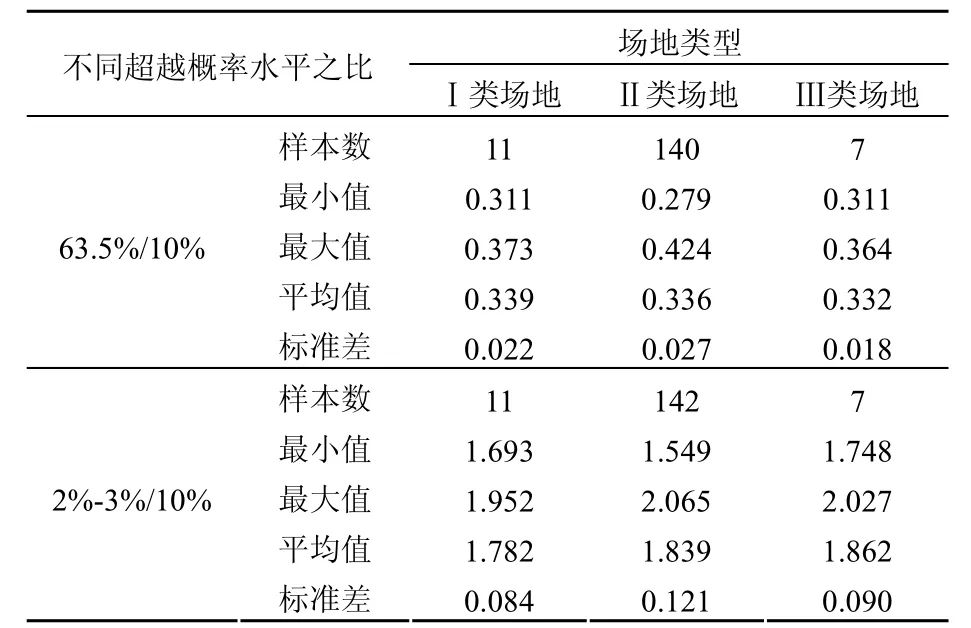
表2 不同场地条件50年不同超越概率水平下的峰值加速度比值

3 场地地震放大效应结果分析

根据收集到的158个工程场地土层地震反应的计算结果，结合《建筑抗震设计规范》对场地的分类，统计不同场地 50年超越概率 63.5%、10%、2%-3%的地面峰值加速度与其对应的基岩峰值加速度的比值（表3）。

表3 场地峰值加速度与其对应的基岩峰值加速度的比值

上述数据表明：对于不同的场地类型，其地震反应的放大倍数亦不同。

（1）对Ⅰ类场地，50年超越概率63.5%的地震反应的放大倍数明显大于50年超越概率10%和2%-3%的放大倍数，说明其具有更为明显的放大效应。而50年超越概率10%与50年超越概率2%-3%的地震反应的放大倍数十分接近。

（2）对Ⅱ类场地，随着超越概率的减少，即地震动强度的增大，地震反应放大倍数呈现逐渐较小的趋势。

（3）对Ⅲ类场地，随着地震动强度的增大，地震反应放大倍数也呈现出逐渐较小的趋势。

Ⅱ类场地与Ⅲ类场地地震放大效应的变化趋势相同的原因可能是：受土的非线性变形特性的影响，地震波能量在土层中传播时耗散，使地表地震动的幅值相对减小，表现为随地震动强度的增大，场地的放大效应降低。

（4）在超越概率相同时，随场地条件变差，其地震反应放大倍数均表现出依次增大的趋势。且表现为Ⅱ类和Ⅲ类场地对基岩峰值加速度具有更为明显的放大效应。

4 结论与讨论

通过以上数据的分析可以得出以下结论：

（1）50年超越概率63.5%与50年超越概率10%的基岩峰值加速度比值的平均值为0.304，标准差为0.031。50年超越概率2%-3%与50年超越概率10%的基岩峰值加速度比值的平均值为1.867，标准差为0.125。

（2）50年超越概率63.5%与50年超越概率10%的场地设计地震动峰值加速度比值，其平均值随场地条件变差呈现出缓慢减小的趋势。50年超越概率2%-3%与50年超越概率10%的场地设计地震动峰值加速度的比值，其平均值随场地条件变差呈现出缓慢增大的趋势。

（3）对Ⅰ类场地，50年超越概率63.5%的地震反应的放大倍数明显大于50年超越概率10%和2%-3%的放大倍数，表现为其具有更为明显的放大效应。而 50年超越概率 10%与 50年超越概率2%-3%的地震反应的放大倍数十分接近。

（4）对Ⅱ类场地和Ⅲ类场地，随着地震动强度的增大，地震反应放大倍数均呈现出逐渐较小的趋势。

（5）在超越概率相同的条件下，随场地条件变差，其地震反应放大倍数均表现出依次增大的趋势。且表现为Ⅱ类和Ⅲ类场地对基岩峰值加速度具有更为明显的放大效应。

由于影响峰值加速度的因素非常复杂，如震源机制，传播途径，震级，震中距，地震波的反射、折射、散射、聚焦以及场地条件等，再者本文所采用的样本数据均来源于甘肃省内的场地安全性评价报告，其结论的适用范围可能仅限于本省。为扩大其适用范围，还需对其他地区的地震动参数及诸多因素综合考虑做进一步的研究。此外，样本数量的局限性，可能也会对本文的结论产生一定的影响。

[1]中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.建筑抗震设计规范（GB 50011-2010）[M].北京：中国建筑工业出版社,2010.

[2]胡聿贤.地震工程学[M].北京：地震出版社,2006.

[3]劭广彪.近断层海底土层地震液化及侧移研究[M].青岛：中国海洋大学，2005:19-21,31-36.

[4]郝敏，谢礼立.集集地震等震线和PGA、PGV等值线关系的研究[J].地震工程与工程震动, 2006,26(1):18-21