某核电站导流堤地基液化及地震永久变形分析
2011-01-27王桂萱周金领
赵 杰,郑 洋,王桂萱,周金领
(大连大学土木工程技术研究与开发中心,辽宁 大连 116622)
0 引言
液化是一种主要的地基基础震害。地震时场地液化现象属于广义的土-结构物的动力相互作用问题,是一个涉及土动力学、结构动力学、非线性振动理论、地震工程学、岩土及结构抗震工程学、计算力学及计算机技术等众多学科的交叉性研究课题,也是一个涉及非线性、大变形、接触面、局部不连续等当代力学领域众多理论与技术热点的前沿性研究课题[1]。
在地震反应分析中,大多采用总应力分析法,但总应力法没有考虑平均法向有效应力的减少对剪切模量的影响,而且不能求出地震过程中孔隙水压力的增长规律和液化随着时间的发展过程[2]。有效应力与总应力法不同的地方就是考虑振动孔隙水压力的增长和变化过程。Finn等人首先提出在粘弹性模型基础上进行有效应力动力分析,但只限于一维的地基水平振动;沈珠江院士把它推广用于二维问题的分析[3];汪闻韶[4]、谢定义等人[5]将孔压与某种应变(如体应变、剪应变)结合起来,建立了孔压的发展模式;Ishihara等[6]提出了孔隙水压力发展的有效应力路径模式,能清晰地反应出砂土从振动到液化的所经历的应力路径。有效应力动力分析方法是在有限单元法的基础上,分时段将以Boit理论为基础的静力计算和以等效线性理论为基础的理论计算结合起来进行分析,其中考虑到了振动引起的孔隙应力的增长、扩散和消散作用[7]。这种方法在计算结果更合理,也能真实的反应出土的特性。
本文基于沈珠江院士提出的二维有效应力动力分析方法,结合Biot动力固结理论,采用自行开发的有效应力动力分析程序分析某核电站导流堤地基砂土液化问题,计算其永久变形,并给出相应的加固措施。
1 动力计算理论
1.1 基本理论
有效应力方法的基本思想是把整个动力作用过程分成若干时段(例如对于地震过程分10~20时段,每时段1 s左右),每个时段的动力分析仍按Wilsonθ法进行,但算完后尚须按某一经验公式计算该时段内各单元的残余变形或孔隙压力的增加,并把它们转化成初应变或初应力后按Biot固结理论进行静力计算,得出结点位移、单元应变和有效应力的变化。如此一个时段一个时段地进行计算,得出整个过程中动应力应变及有效应力(孔隙压力)和残余变形的发展过程。
1.2 计算模式
本次动力计算采用沈珠江院士推广的一般情况下的等价粘弹性模型。某一荷载循环下的动剪切模量 G、阻尼系数λ、残余体应变增量Δε及残余剪应变增量Δγ按以下公式计算:
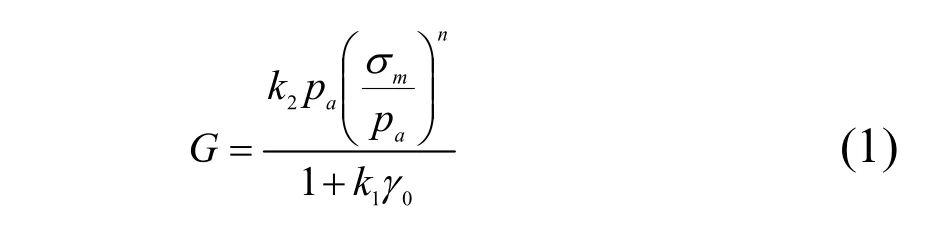
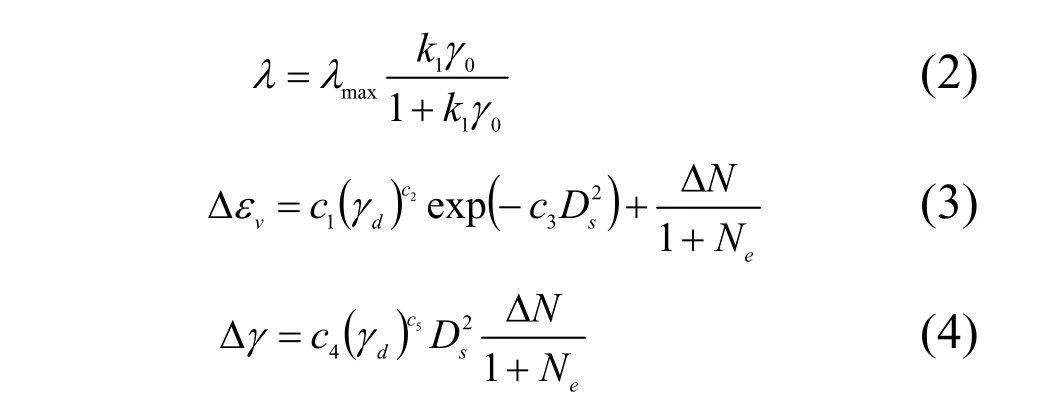
式中参数k1、k2和λmax通过共振柱或动三轴的模量试验测定;参数 c1、c2、c3、c4、 c5则通过常规的动三轴液化试验测定。
2 工程概况与抗震设计
2.1 工程概况
导流堤长2 063.1 m,堤顶高程为4.40 m,堤顶宽度为5.5 m。堤心采用1~500 kg开山石,堤身采用爆破排淤填石法成堤,外坡、内坡坡度1:1.5。为防止堤前波浪底流速的冲刷作用,堤内、外侧抛填100~150 kg块石护底。北导流堤根部约400 m范围兼作取水头部干施工围堰,打设0.8 m厚柔性地连墙做防渗结构。取水明渠导流堤地基土上存在较厚的粉砂层。图1为导流堤剖面图。
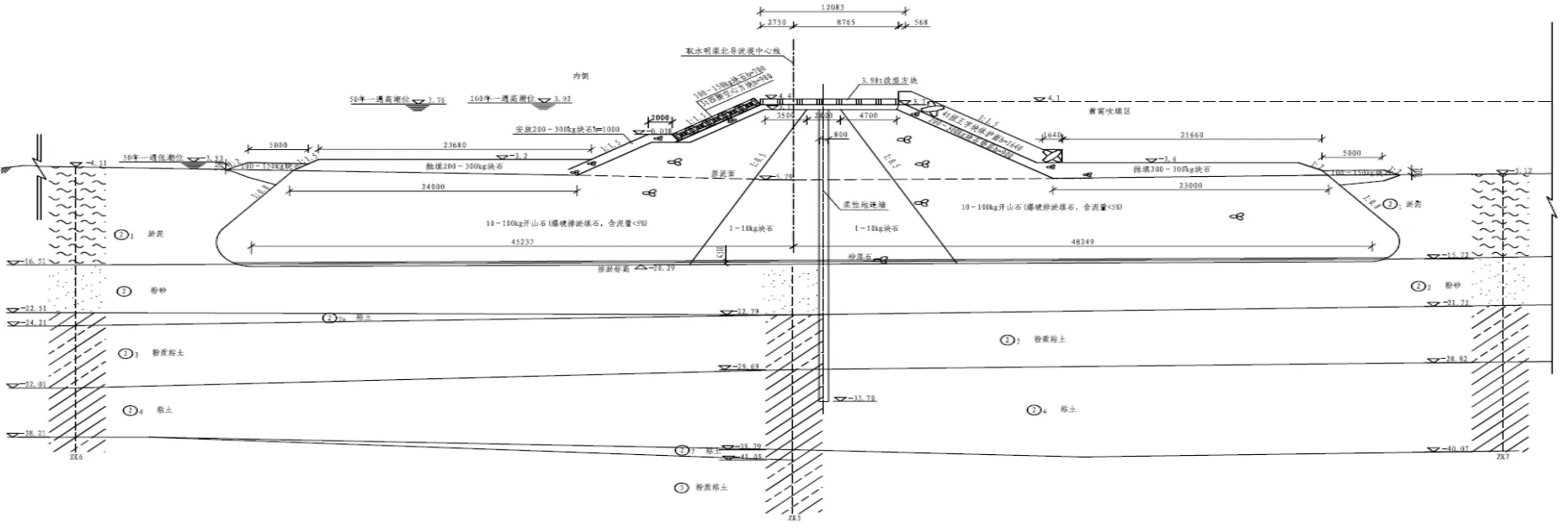
图1 取水明渠导流堤剖面图Fig.1 Cross section of the diversion dike.
2.2 抗震标准
厂址的抗震设防烈度为Ⅶ度,设计基本地震加速度值为 0.10 g。根据《核电厂抗震设计规范》(GB50267-97)[8],取水明渠导流堤确定为非核安全级、抗震Ⅲ类物项,抗震设计按港工构筑物抗震标准设计。考虑到导流堤的重要性,采用极限安全地震动SL-2进行抗震检验。抗震设计遵照《水运工程抗震设计规范》(JTJ225-98)[9]有关规定。本次计算在SL-2级地震动作用下,计算导流堤地基液化及永久变形。
3 计算条件
本次计算采用二维平面模型,图2、3给出了导流堤断面计算模型及单元网格,本次分析共剖分 3 481个单元,3 622个节点。计算的本构关系采用等 价粘弹性模型。
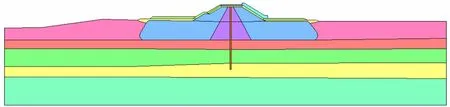
图2 导流堤断面计算简图Fig.2 Sketch of calculation section of the diversion dike.
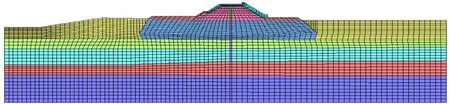
图3 导流堤断面单元网格Fig.3 Element mesh for the diversion dike.
3.1 计算范围及边界条件
计算范围:防波堤左右各取100 m为计算范围,深度方向取50 m,可以取到整覆盖土层。在动力计算中,主要考虑地震作用产生的水平剪切变形,在动力计算时,地基两侧竖向约束,水平向自由;地基底部边界假定水平及竖向均固定。
3.2 计算参数
本次静动力计算见表1及表2。
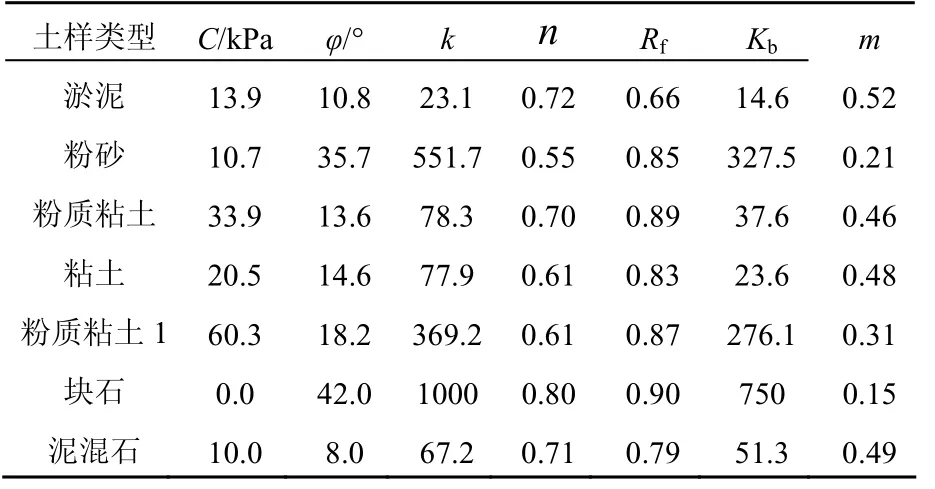
表1 力计算参数
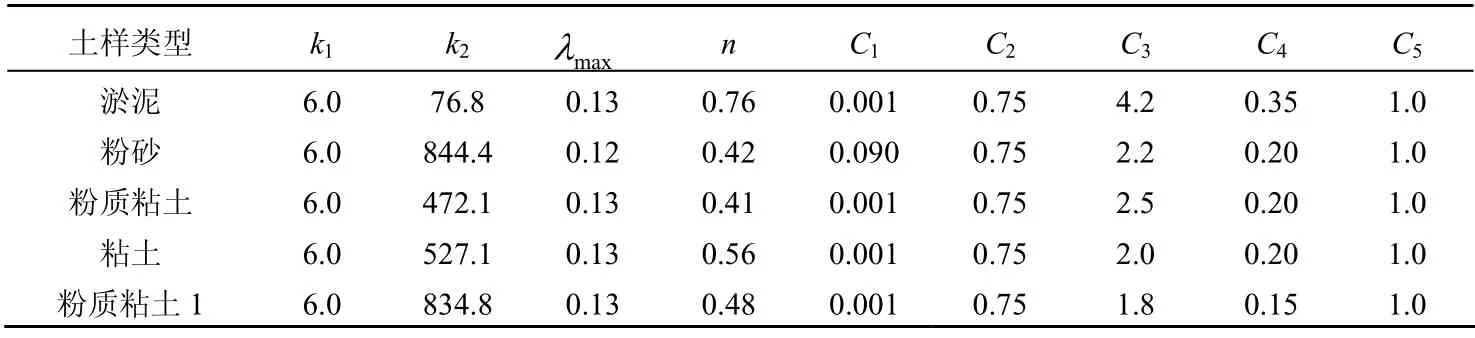
表2 动力计算参数
3.3 地震波的选择
根据场地地震安评资料,SL-2级基岩水平峰值加速度设计值取0.02 g,竖向峰值加速度取0.134 g。厂址时程地震波的地震动持时41 s,地震动时程曲线如图4。
4 计算结果及分析
4.1 地震液化分析
在地震作用下,单元的孔隙水压力逐渐增加,相应的有效应力逐渐减小,当有效应力为0时,则认为该单元发生液化。本文采用此法进行液化判别,单元的平均有效应力采用如下公式计算:
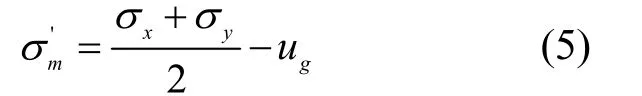
图5给出了导流堤断面在极限地震作用下的液化区分布图,图中黑色部分为液化区。从图中可以看出,在Sl-2级地震作用下,粉砂层发生了大面积液化。
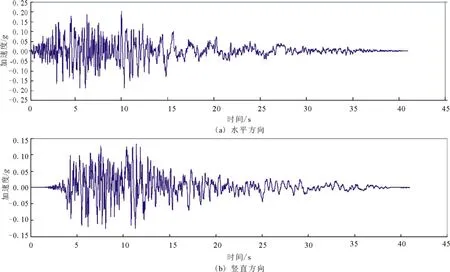
图4 地震动时程曲线Fig.4 Time history curves of the site seismic wave.
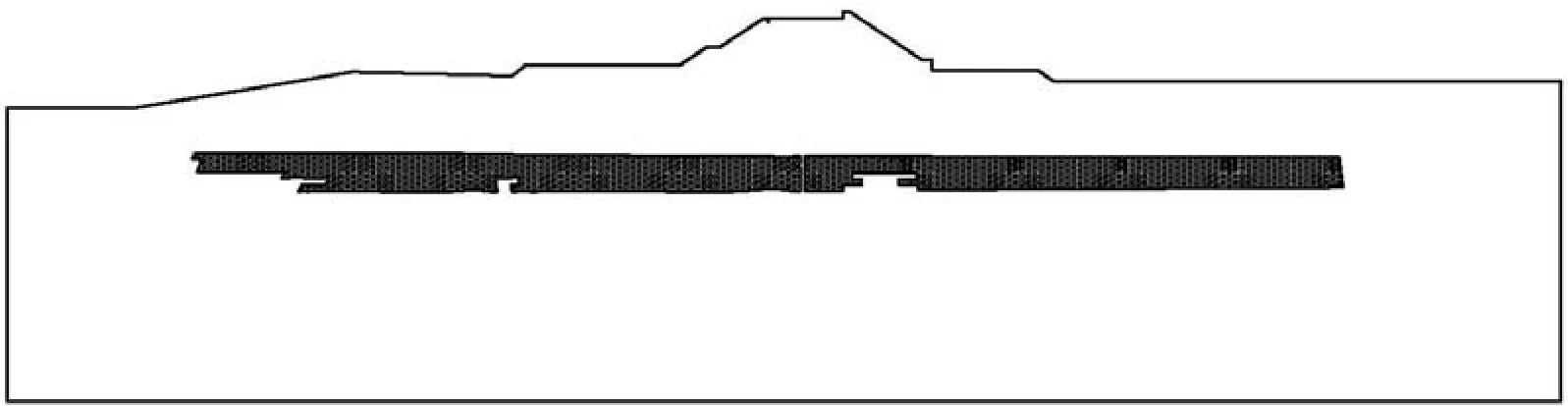
图5 导流堤断面液化区分布图Fig.5 Distribution of liquefation area in the diversion dike.
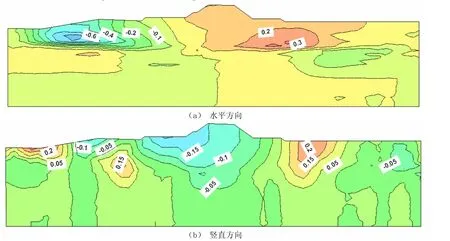
图6 导流堤断面永久变形分布图Fig.6 Distribution of permanent deformation on the section of the diversion dike.
4.2 地震永久变形分析
图6给出了极限地震动作用下,导流堤水平及竖向的永久变形等值线云图。计算得出导流堤水平永久变形量为73 cm,竖向永久变形量为23 cm。从图中可以看出,随着地基土深度的增加,地震永久变形量逐渐减小。在地震开始的20 s内,地震永久变形量增长幅度较大,20 s之后永久变形量继续增加,但增长幅度变小。
5 结语
本文介绍了基于等价粘弹性模型的二维有效应力动力有限元分析方法,并且采用该方法对某核电站导流堤工程进行动力分析,给出导流堤液化区分布情况及地震永久变形。由计算结果可知:
(1) 在极限地震动作用下,导流堤砂土层会发生大面积液化,建议通过振冲挤密、置换或者水泥土搅拌等方式进行地基处理,以消除液化的影响。
(2) 在地震作用下,导流堤水平永久变形量为73 cm,竖向永久变形量为23 cm,导流堤左右宽度为190 m,地震产生的永久变形不至于使导流堤整体向渠心滑移,不会影响到核电厂安全用水。
[1]方志, 陆浩亮, 王龙. 土-结构动力相互作用研究综述[J]. 世界地震工程, 2006, 22(1): 57-63.
[2]徐志英, 沈珠江. 地震液化的有效应力二维动力分析方法[J]. 河海大学学报(自然科学版), 1981, (3):1-14.
[3]朱百里, 沈珠江. 计算土力学[M]. 上海: 上海科学技术出版社,1990.
[4]汪闻韶. 饱和砂土振动孔隙水压力试验研究[J]. 水利学报, 1962,(2):36-47.
[5]谢定义, 张建民. 往返荷载下饱和砂土强度变形瞬态变化的机理[J].土木工程学报,1987,20(3):50-70.
[6]Ishihara K. Undrained deformation and liquefaction of sand under cyclic stress[J]. Soils and Foundation, 1975, 15(1):29-44.
[7]周健, 白冰, 徐建平. 土动力学理论与计算[M]. 北京, 中国建筑工业出版社, 2001.
[8]国家地震局. GB50267-97核电厂抗震设计规范[S].北京:国家地震局,1997.
[9]中华人民共和国交通部.水运工程抗震设计规范[S]. 北京:人民交通出版社,1999.
