离散元微观参数对砂土宏观参数的影响

申志福，蒋明镜，朱方园，胡海军

(1.同济大学地下建筑与工程系，上海 200092；2.同济大学岩土及地下工程教育部重点实验室，上海 200092）

0 引 言

离散单元法是上世纪70年代由Cundall[1]提出并逐步发展起来的一种数值计算方法，它将介质看做一系列离散单元体的组合，单元体运动受牛顿经典力学定律控制。离散单元法分析中假设颗粒单元为刚性体，接触发生在很小范围内，接触处允许有一定重叠量，重叠量大小与接触力和接触刚度有关。颗粒间的接触和相互作用关系通过粒间接触模型控制。该方法现已大量运用于岩土体数值分析。为了研究不同特性的岩土体，各国学者提出了多种颗粒接触模型，如理想线弹性接触模型，Hertz-Mindlin非线性模型[2]，Iwashita K等[3]提出的抗转动模型，蒋明镜等[4]提出的考虑毛细水的接触模型等。颗粒接触刚度和粒间摩擦系数是这些模型中两个最基本的参数，也是离散元参数标定过程中的主要调整参数。

从离散元计算过程来看，颗粒接触刚度大小决定着计算时步。计算时步太大，离散元计算精度下降；时步太小结果波动大且计算时间延长[5]。从计算结果来看，颗粒接触刚度和粒间摩擦系数对土体宏观力学参数如初始切线模量、内摩擦角有着很大影响，只有恰当的微观参数取值才可能得到与实际接近的数值计算结果。因此合理地选定微观参数对离散元模拟的效率和结果可信度都至关重要。

目前，离散元微观参数的选取有多种方法。武力等[6]将遗传神经网络与三轴试验离散元数值模拟有机结合，用于改性砂土颗粒离散元接触模型参数反演；邢纪波等[7]根据离散单元中的应力波传播条件确定粒间接触刚度的理论公式；周健等[8]针对颗粒流仿真试样的细观力学特征与物理试样宏观力学响应之间的关系进行了参数研究,并揭示了一些规律；徐小敏等[9]利用颗粒材料单元体宏观力学参数和颗粒细观参数间的相关性，通过室内三轴试验的模拟和结果的回归分析，建立了宏微观参数间的经验公式。本文运用二维离散元商业软件Particle Flow Code（PFC2D）进行66组双轴压缩实验以探讨两种不同孔隙比（分别代表密砂和松砂）试样的粒间接触刚度和摩擦系数对试样初始切线模量（后文均称为弹性模量）和内摩擦角的影响。

1 双轴实验设计

1.1 接触模型选择

因本文只针对颗粒接触刚度和粒间摩擦系数两个微观参数对宏观参数的影响规律进行分析，不针对特定土体进行参数标定，故接触模型采用简单的线弹性接触模型，不考虑粒间胶结作用。在 PFC中，颗粒间线性接触模型如图1所示：

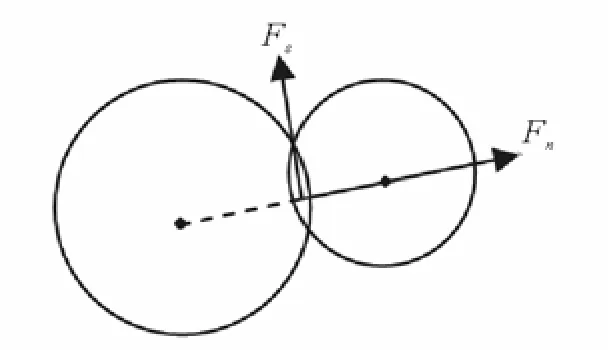
图1 粒间线性接触模型Fig.1 Interparticle linear contact modle of PFC20.

粒间法向接触力采用全量法计算，由相对法向位移和法向接触刚度决定：

式中 Fn为法向接触力；kn为法向接触刚度；Un为法向相对位移。

粒间切向接触力采用增量法计算，由相对切向位移增量和切向接触刚度决定：

式中ΔFs为切向接触力增量；ks为切向接触刚度；ΔUs为切向相对位移增量。

当颗粒间无胶结时，切向力不能大于颗粒间摩擦系数与法向力的乘积：

式中Fs为切向接触力；μ为粒间摩擦系数。

1.2 成样参数及试验方案

双轴试验的模拟过程分为成样，固结和压缩三部分。成样方法采用蒋明镜等[10]提出的分层欠压法。为使试样整体均匀，该方法将试样分层生成，新的一层颗粒生成后试样的平均孔隙比较前几层平均孔隙比小，最后一层生成后试样整体达到目标孔隙比。该方法通过调节试样孔隙比可形成松砂、中密砂及密砂试样，同时能避免成样过程中出现上松下密的现象。

本实验共生成两种孔隙比试样：0.21和0.25，分别代表密砂和松砂。密砂样和松砂样颗粒总数目均为6 000,直径 6～9 mm,颗粒密度均为 2 600 kg·m-3。为能达到目标孔隙比，密样成样过程中粒间摩擦系数为0.1，松样为1.0，颗粒与墙之间的摩擦系数均为 0。成样过程中采用的最优孔隙比如下：密样为ep(1)=0.233， ep(1+2)=0.228， ep(1+2+3)=0.225,ep(1+2+3+4)=0.219，ep(1+2+3+4+5)=0.21；松样为ep(1)=0.27， ep(1+2)=0.269，ep(1+2+3)=0.265,ep(1+2+3+4)=0.259，ep(1+2+3+4+5)=0.25。离散元双轴压缩试验成样过程参数见表1。生成试样级配曲线如图2所示。

表1 试样参数

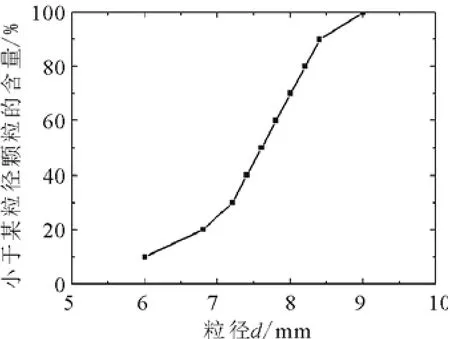
图2 颗粒级配图Fig.2 Distribution of grain size.

成样后分别在100 kPa，200 kPa和400 kPa围压下等向固结；固结后竖向加压；以10%/min的速率剪切；采用伺服方式保持围压稳定；实验采用刚性边界。在剪切过程中记录试样的轴向应力、轴向应变、体变和孔隙比。

为了探究微观参数（颗粒接触刚度和颗粒间摩擦系数）对宏观参数（弹性模量和内摩擦角）的影响，剪切过程按表2方案进行：

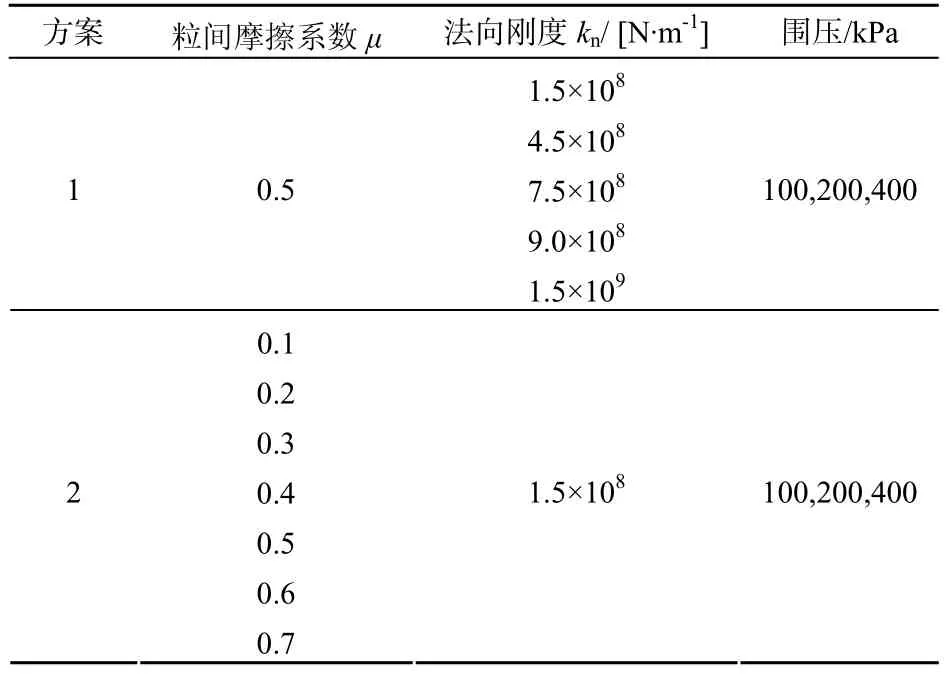
表2 双轴实验方案

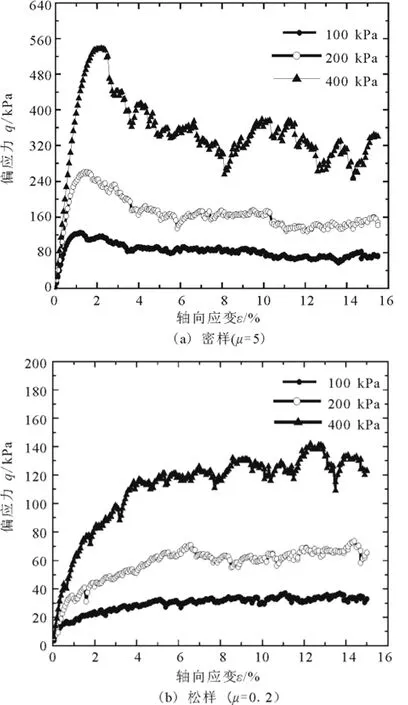
图3 松、密沙的应力—应变关系曲线（kn=1.5×108 N·m-1，ks=1.0×108 N·m-1）Fig.3 Stress-strain relationship curves of loose and dense sands.

(1) 维持摩擦系数不变，在保证kn/ks=1.5下改变法向接触刚度，在100 kPa，200 kPa和400 kPa围压下剪切；

(2) 维持粒间接触刚度不变，改变粒间摩擦系数，在100 kPa，200 kPa和400 kPa围压下剪切，其中密样μ变化范围为0.1～0.7，松样μ变化范围为0.1～0.5。

2 模拟结果分析

2.1 应力应变关系

密样和松样的典型应力应变关系和体变关系如图3、4所示。

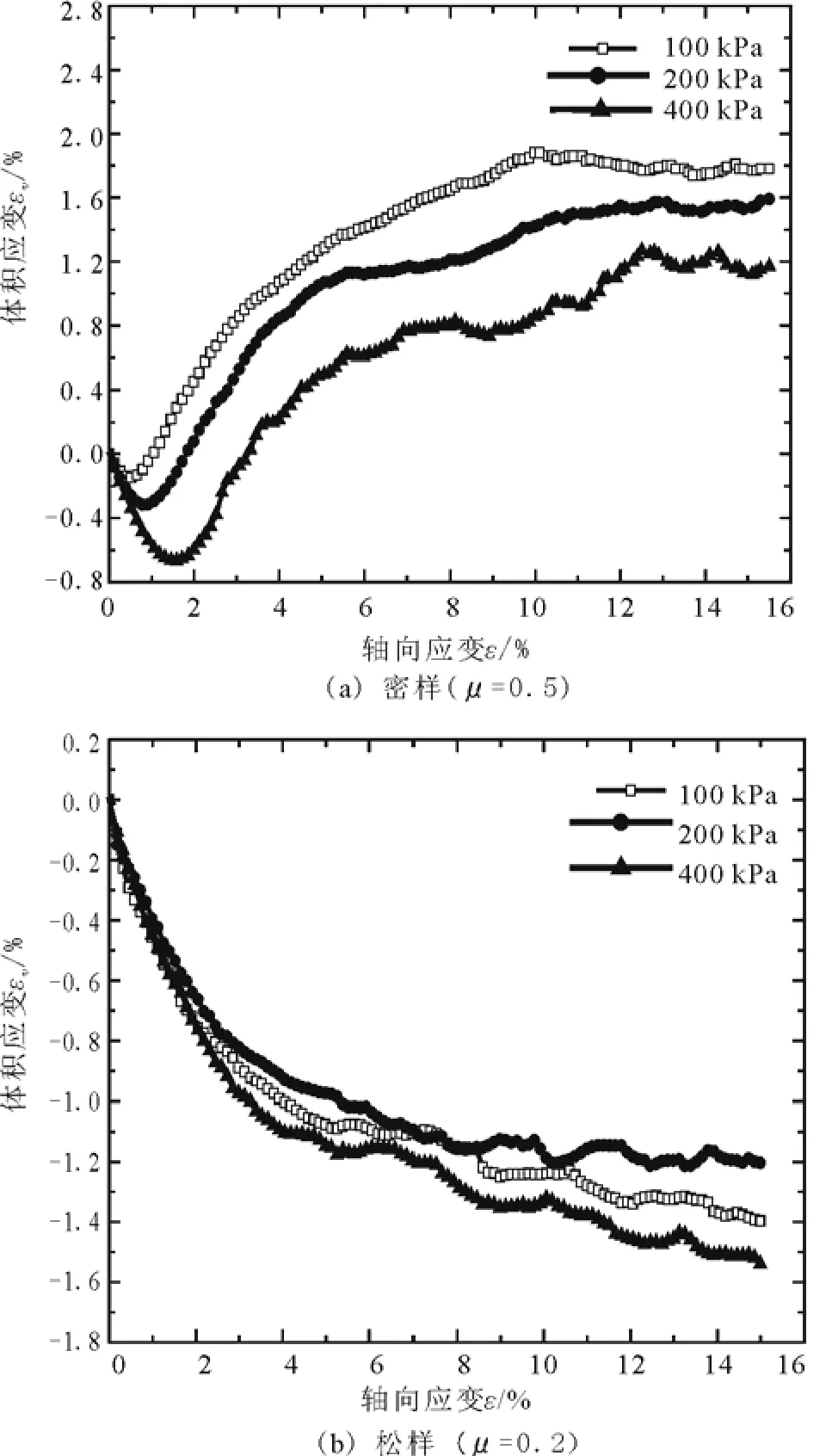
图4 松、密砂的体变—轴向应变关系曲线（kn=1.5×108 N·m-1，ks=1.0×108 N·m-1）Fig.4 Volumetric strain-axial strain relationship curves of loose and dense sands.

从图3（a）可见，密样的应力应变关系为软化型：不同围压下的应力均先随轴向应变的增大而增大，在轴向应变为1%～2%时达到强度峰值后迅速减小，最终趋于稳定。由于颗粒较少，在400 kPa高围压下峰值后应力波动较明显。从图4（a）可见，各围压下密样的体变随轴向应变的变化均表现出先剪缩后剪胀的特性，即在轴向应变为1%～2%时达到剪缩最大值后剪缩量逐渐减少进而表现出剪胀，剪胀体变随轴向应变增大而渐趋稳定。这些都是密砂的典型力学特性。

从图3（b）可见，松样的应力应变关系为硬化型：各围压下应力均随轴向应变增大而增大，增长趋势渐趋平缓。由于颗粒较少，在400 kPa高围压下应力波动较明显。从图4（b）可见，各围压下体变均表现为剪缩，剪缩体变随轴向应变增大而增大且增长趋势渐缓。这些都是松砂的典型力学特性。

2.2 接触刚度变化对宏观参数的影响

按照表2中第1组试验方案，维持摩擦系数不变，在保证 kn/ks=1.5情况下改变法向接触刚度进行双轴试验得到试样弹性模量、内摩擦角与法向接触刚度之间的关系，如图5、6所示。

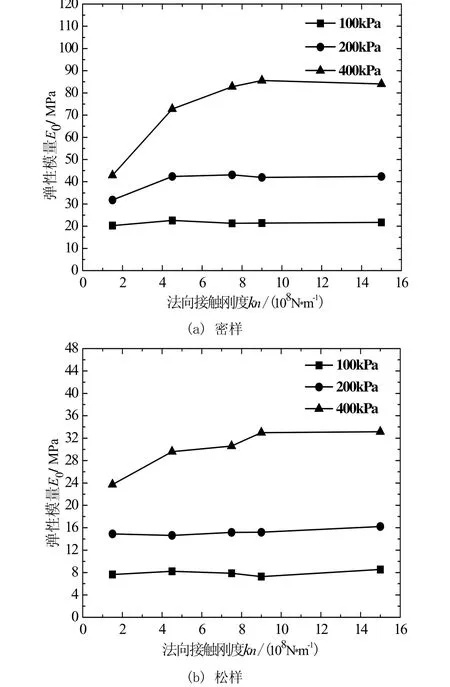
图5 弹性模量—法向接触刚度关系曲线Fig.5 Young’s modulus-normal stiffness relationship curves of loose and dense sands.

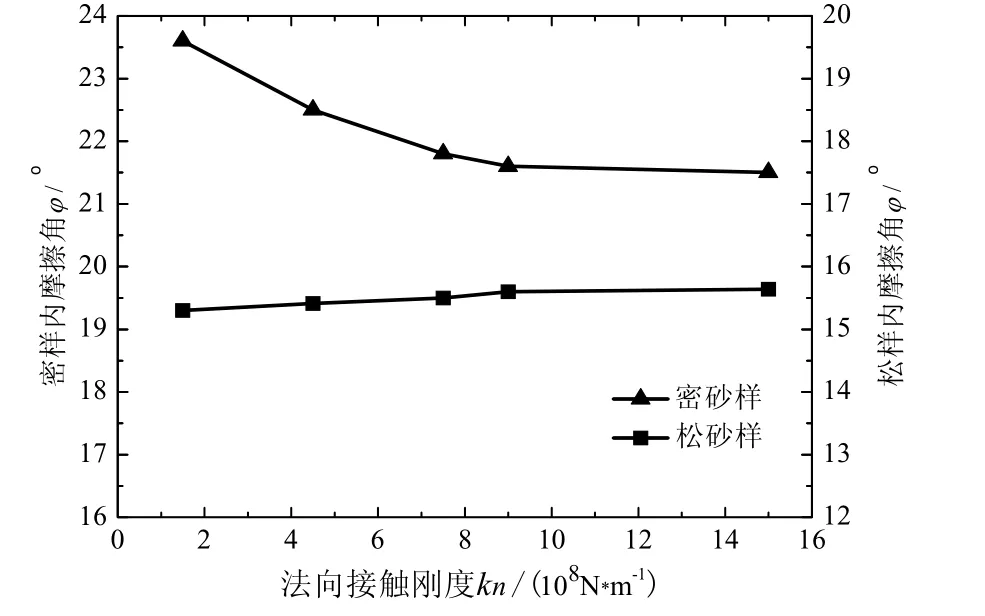
图6 内摩擦角—法向接触刚度关系曲线Fig.6 Friction angle-normal stiffness relationship curve.

对于密样，从图5(a)中可以看到，在相同刚度下，围压越大弹性模量越大；在100 kPa和200 kPa较低围压下接触刚度变化对试样弹性模量的影响并不明显；在400 kPa高围压下，当接触刚度从1.5×108N·m-1变化到1.5×109N·m-1时，弹性模量从42.9 MPa增长到84 MPa,增长了近一倍。从图6中可以看到，刚度变化对密样摩擦角的影响表现为随刚度增大内摩擦角逐渐减小的特点，从23.6°减小到21.5°，减小了9%，但整体上减小不多，内摩擦角受刚度影响很小。

对于松样，从图5(b)中可以看到，在相同刚度下，围压越大弹性模量越大；与密样相似，在100 kPa和200 kPa较低围压下弹性模量基本不受刚度变化的影响；在400 kPa高围压下试样弹性模量随接触刚度增大而有明显增大，当接触刚度从1.5×108N·m-1变化到1.5×109N·m-1时，弹性模量从23.8 MPa增长到33.2 MPa，增大了40%。从图6可以看到，松样的内摩擦角随刚度增大从15.3°增大到15.6°，增幅很小，内摩擦角基本不受刚度变化的影响。

由以上结果看到，颗粒接触刚度对试样弹性模量的影响在100 kPa和200 kPa低围压下很小，在400 kPa高围压下影响较明显。这里需要指出的是，以上结论是在考虑了颗粒重叠量的情况下得到的。在离散元数值模拟中，颗粒允许发生一定的重叠量，但重叠量必须控制在允许的范围内，因为实际砂土颗粒间的挤压变形量非常小，故粒间接触刚度不能取得太小。为分析重叠量与接触刚度间的关系，在法向刚度分别为 1.5×107N·m-1、7.5×107N·m-1、1.5×108N·m-1、4.5×108N·m-1和7.5×108N·m-1五种情况下进行密砂双轴试验得出了如图7所示的颗粒最大重叠量与法向接触刚度间的关系。图中最大重叠量是指试样中相邻两颗粒重叠区域宽度最大值与平均粒径（7.5 mm）的比值。

从图7可以看出，在相同刚度下，围压越大，粒间最大重叠量越大；在相同围压下，随法向接触刚度增大，最大重叠量有显著减小。本文以 45‰作为重叠量最大允许值，要保证在各围压下重叠量都不超过图7中的控制线，接触刚度至少为1.5×108N·m-1。考虑了重叠量影响后，各刚度下的重叠量在100 kPa和200 kPa低围压下变化不大，在400 kPa高围压下变化较为明显，这也是上述弹性模量随接触刚度变化规律的微观解释。

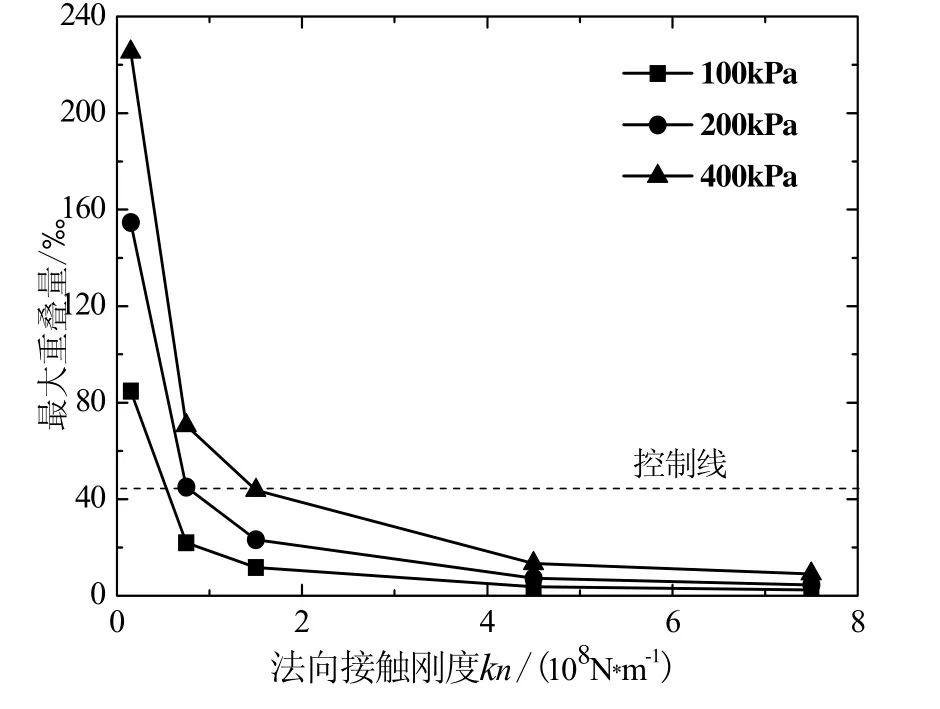
图7 重叠量—法向接触刚度关系曲线Fig.7 Overlap-normal stiffness relationship curves.

2.3 粒间摩擦系数变化对宏观参数的影响

按照表2中第2组试验方案，维持粒间接触刚度不变，改变粒间摩擦系数进行双轴试验，得到试样弹性模量、内摩擦角与粒间摩擦系数之间的关系，如图8、9所示。

对于密样，从图8(a)中可以看到，各围压下试样弹性模量随摩擦系数的增大而增大，增长趋势渐缓；在100 kPa、200 kPa和400 kPa下，当摩擦系数由0.1增加到0.7时，弹性模量增幅分别为51%、56%和65%，这说明粒间摩擦系数对弹性模量有较明显影响。从图9中可以看到，试样内摩擦角随粒间摩擦系数的增大几乎呈线性增大，从12.1°增加到26°，反应了颗粒间摩擦作用对密砂强度的显著影响。

对于松样，从图8(b)中可以看到，弹性模量随摩擦系数增大而增大，弹性模量的增幅在较大摩擦系数时有明显增大且围压越大这种增大的趋势越明显。在100 kPa、200 kPa和400 kPa下，当摩擦系数由0.1增加到0.5时，弹性模量分别增加了1.24倍、1.66倍和2.55倍，说明摩擦系数对松样弹性模量的影响比密样大得多。从图9中可以看到，松样的内摩擦角随摩擦系数的增大而增大，当摩擦系数较大时增大的幅度有所减缓；当摩擦系数由0.1增加到0.5时，内摩擦角从10.9°增加到15.3°，说明摩擦系数对松砂强度有明显贡献。

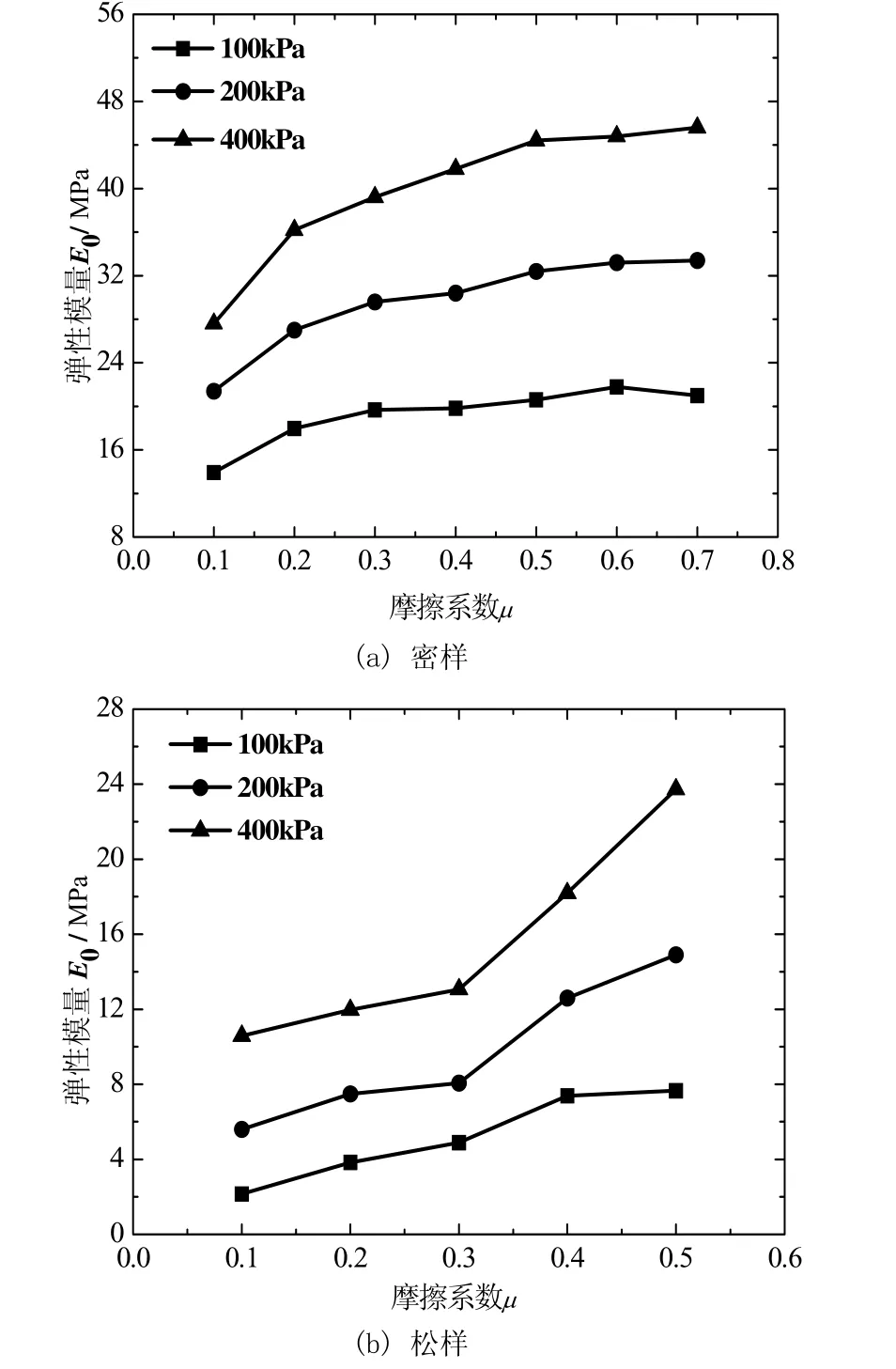
图8 弹性模量—摩擦系数关系曲线Fig.8 Young’s modulus-frictional coefficient relationship curves of loose and dense sands.

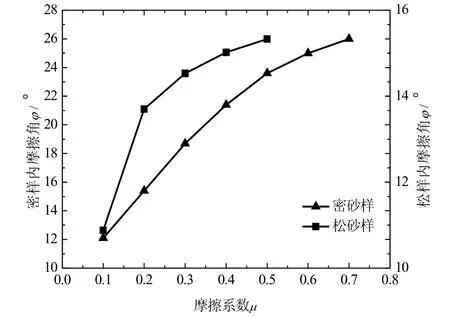
图9 内摩擦角—摩擦系数关系曲线Fig.9 Friction angle-frictional coefficientrelationship curves for both loose and dense sands.

2.4 离散元数值计算参数选取建议

由以上结果可以看出，无论密样还是松样，两个离散元微观参数各自对宏观力学参数的影响程度是不同的，可形象地用图10说明。微观参数对宏观参数的影响程度用箭头表示，箭头越大颜色愈深，表示影响程度越大。从图中可以看到，对于微观参数，粒间摩擦系数对宏观参数的影响较颗粒接触刚度产生的影响大；对于宏观参数，初始切线弹性模量受到粒间摩擦系数影响较受到接触刚度的影响大，内摩擦角则主要由粒间摩擦系数控制而基本不受接触刚度影响。

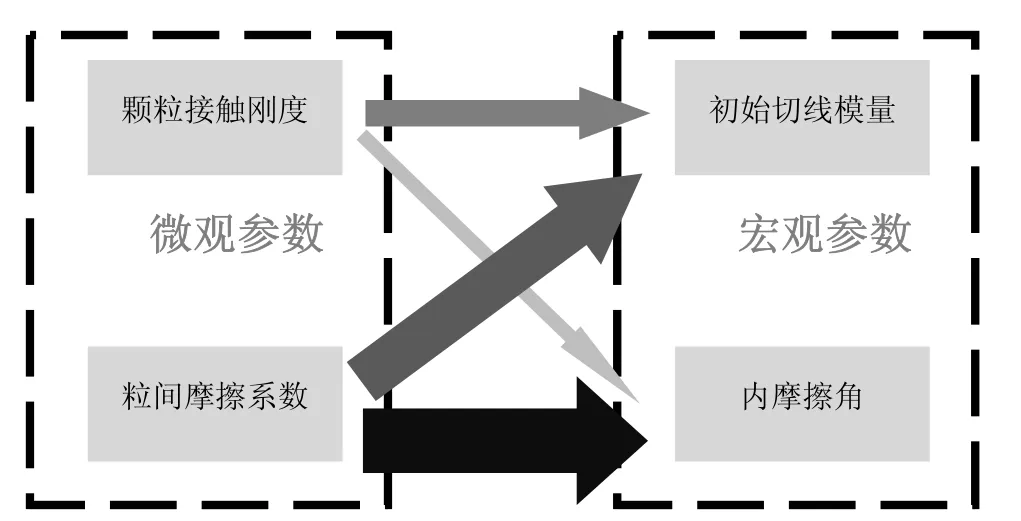
图10 微观参数对宏观参数影响Fig.10 Sketch of influence of micro-parameters on macro-parameters.

在进行离散元数值模拟时，可通过图10的规律合理选取、调整微观参数。由于接触刚度对宏观参数影响较粒间摩擦系数产生的影响小得多，故可考虑调整接触刚度的取值，如选取较小的接触刚度以增大计算时步提高效率而不致引起宏观参数的太大变化；但刚度不能太小，否则重叠量过大，影响计算可信度，建议法向接触刚度不宜小于1.5×108N·m-1。粒间摩擦系数因对宏观参数影响显著，故当模拟结果与目标结果出入较大时调整摩擦系数将使参数调整效果更为明显有效。

3 结论

本文运用PFC2D通过66组双轴压缩试验对密砂样和松砂样进行了离散元模拟，探究了颗粒接触刚度和粒间摩擦系数两个微观参数对土体初始切线弹性模量和内摩擦角的影响，得出以下结论：

(1) 当考虑了颗粒重叠量限制后，在400 kPa较高围压下，粒间接触刚度对密样和松样弹性模量均有一定程度影响且对密样影响大于松样；在100 kPa和200 kPa较低围压下密样和松样弹性模量均基本不受接触刚度影响。

(2) 粒间接触刚度对密样和松样的内摩擦角均影响很小。

(3) 粒间摩擦系数对密样和松样弹性模量都有明显影响且对松样的影响大于密样。

(4) 粒间摩擦系数对密样和松样的内摩擦角均有非常显著影响。

[1]Cundall P A. A Computer Model for Simulating Progressive Large Scale Movements in Blocky Rock System[C]//Proceedings of the Symposium of the International Society of Rock Mechanics. Nancy, France: [s.n.],1971.

[2]Mindlin R D, H Deresiewicz. Elastic Spheres in Contact under Varying Oblique Forces[J]. Journal of Applied Mechanics, 1953, 20(3): 327-344.

[3]Iwashita K, Oda M. Rolling Resistance at Contacts in Simulation of Shear Band Development by DEM[J]. Journal of Engineering Mechanics,1998,124(3): 285-292.

[4]Jiang M J, Leroueil S., Konrad J M. Insight into Shear Strength Functions of Unsaturated Granulates by DEM Analyses[J]. Computers and Geotechnics,2004, 31(6):473-489.

[5]焦红光，李靖如，赵继芬，等. 关于离散元法计算参数的探讨[J]. 河南理工大学学报(自然科学版), 2007, 26(1): 88-93.

[6]武力，屈福政，李守巨. 土压平衡盾构改性砂土离散元模型参数反演方法研究[J]. 大连理工大学学报,2010, 50(6): 860-866.

[7]邢纪波，俞良群，张瑞丰，等. 离散单元法的计算参数和求解方法选择[J]. 计算力学学报, 1999, 16(1): 47-51, 99.

[8]周健，廖雄华，池永，等.土的室内平面应变试验的颗粒流模拟[J].同济大学学报, 2002, 30(9):1044-1050.

[9]徐小敏，凌道盛，陈云敏，等.基于线性接触模型的颗粒材料细–宏观弹性常数相关关系研究[J].岩土工程学报, 2010,32(7):991-998.

[10]Jiang M J, Konrad J M, Leroueil S. An Efficient Technique for Generating Homogeneous Specimens for DEM Studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597.