分形几何在岩土力学研究中的过去、现在与未来

林沛元，汤连生，桑海涛，邓锡斌，吴 科，邓钟尉

（1.中山大学地球科学系, 广东 广州 510275;2.广东省地质过程与矿产资源探查重点实验室, 广东 广州 510275）

0 引言

岩土力学的复杂性源于其研究对象—岩土材料的特殊性。岩土体是多相多组分不连续的开放系统，系统的应力历史、各组分间的物理化学作用及周围环境的作用导致岩土材料力学行为具有不确定性、不规则性与模糊性。长期以来，岩土力学工作者致力于采用理想化的数学或力学模型描述岩土这类无规则性、随机性系统并试图预测其力学行为，但结果往往不甚理想，甚至出现较大偏差。因此，岩土力学的理论研究急需新的思想，新的方法和新的技术[1]。

分形理论由法国数学家 Mandelbrot创立[2_3]，是上个世纪70年代自然科学的三大发明之一，是描述自然界非线性特征及行为强有力的工具。目前分形理论已广泛应用到物理学、化学、地理学、地质学、生物学等自然科学领域的研究中，甚至哲学、经济学、人类的思维等社会科学领域也有涉猎。通过三十几年的努力，分形几何应用于岩土力学的研究取得了一系列的成果，成为解决实际岩土工程问题，开创岩土力学理论研究的一个新的突破口。

本文首先简单介绍分形几何理论，然后阐述分形在岩土力学领域的研究现状，最后探讨其在岩土力学领域的发展方向。

1 分形几何简述

分形几何是研究具有层次结构的系统其局部与整体在形态、功能、信息、时空等方面的自相似性，并以一个或几个维数表征其复杂程度。通常情况下，分数维的值越大，则系统越复杂。有研究指出[4]，软土加固后，其孔隙度分维、孔隙分布分维及孔隙边缘形状分维均有不同程度的降低，表明系统向有序性进化。多重分形系统比单一分形系统复杂。

1.1 分形图形与维数计算

经典的分形模型有 Koch曲线，Cantor集合，Sierpinski地毯和Menger海绵等，如图1-4所示。这些著名的分形图形皆属数学上的分形，具有严格的自相似性质，而自然界中的分形只能是统计意义上的自相似，并且具有无标度区间，即分形特征只存在于一定尺度范围。如云彩形状的分形，只有当测量尺度在100～106km2之间才具有分形特征[5]。

分形理论广泛应用的同时，也为其自身的发展注入了新活力。目前的分形维数主要包括相似维数、容量维数、盒子维数、信息维数、关联维数及广义分形维数6种，孙博玲[6]对此进行了讨论分析，并在此基础上概括了分形维数测量的5种方法，它们分别是改变粗视化程度求维数法，测度关系求维数法，关联函数求维数法，分布函数求维数法和波谱求维数法。不同领域的学者利用不同的分形维数描述不同的研究对象，并采取相应的计算方法进行维数计算。

1.2 分形几何应用的基本方法

谢和平[1]根据国内外的研究成果，将分形几何从理论转向解决实际问题的途径归纳为三个基本方法：（1）分形模型法；（2）实验测定法；（3）维象法。这三类基本方法在岩土力学的分形研究中皆有涉及。岩土材料是四相体系[7]，它包含了大量不同层次的孔隙和微裂纹，结构与海绵体相似，因此常用分形模型法将其结构简化抽象为 Menger海绵模型并进行相关数学分析，由此探寻岩土材料的本征特性。

2 分形在岩土力学中的应用

岩土体的变形、断裂、微裂纹、孔隙、粒度（块度）、渗透率、密度及其物理力学性质均应具有分形特征，这一思想已被大量的实验结果所证实[8_12]。利用分形理论研究岩土力学问题，主要内容包括四个方面：（1）定量描述岩土材料的结构；（2）探讨水在岩土介质中的渗流问题；（3）岩土材料的强度问题；（4）岩土材料的分形力学特征。

图1 Koch曲线（n=1，2，3，5）Fig.1 Koch curves (n=1，2，3，5).

图2 三分Cantor集（n=1，2，3）Fig.2 Cantor sets (n=1，2，3).

图3 随机Sierpinski地毯（n=4）Fig.3 Random Sierpinski Carpet (n=4).

图4 Menger海绵体（n=2）Fig.4 Menger Sponge (n=2).

2.1 结构定量描述

土体结构的分形定量描述归结为三个方面：

(1) 数量—尺寸分形分布模型，讨论孔隙或土颗粒大小的分布特征[13_15]，孔隙分布分形特征可由式(1)[16]表达，而粒度分布的分形模型见式（2）[17]:

式中：D是分形分维，Vp(r)是半径为r的孔隙体积；N(r＞R)为粒径大于R的土颗粒数量。

(2) 表面分形模型，探讨孔隙与固体颗粒界面的分形特征[8,18]。土颗粒并非想象中的圆球状，而是粗糙不平且无规则的。Avnir[19]等通过研究土粒表面积与土粒平均半径的非线性关系，指出土粒表面具有分形特征。二维孔隙土粒界线通常采用 Koch曲线模拟。

(3) 质量分形模型，描述固体颗粒质量分布的分形特征。粒度分布是岩土材料的基本试验项，是岩土体力学性能评估的重要指标之一。由于Turcotte[17]提出的数量—粒径分形模型存在颗粒数量测量上的困难，Tyler[13]改用质量—粒径关系来描述粒度分布：

式中M(r＜R)为粒径小于R的颗粒质量；MT为颗粒总的质量；RT为颗粒的最大粒径。

研究发现，粒度分布的双对数曲线往往为多段折线，具有多重分形特征[20]，仅用一个分维来描述粒度分布特征并不完善，刘晓明等[21]通过分析沉积岩土的成因，在 Tyler工作的基础上采用两个分形维数来描述沉积岩土粒度的分形分布特征，并应用到湖南红层软岩崩解性差异的分析。

岩体结构的分形研究，在孔隙模型上虽与土体模型相似，但其更多的是关注岩体中的节理裂隙分布、节理的粗糙度及岩石破碎后块度的尺寸分布等。岩石碎块无论是源于切割、爆破或是风化，都表现出分形分布特征，具有自相似性或标度不变性。借助重正化群（renormalization group）理论分析岩石破碎特征是岩土力学分形研究的热点。岩石破裂的分形维已被证明可以作为材料破碎过程中断裂阻力的一种度量，实验表明[17]，分形维越小则材料脆性越好。谢和平在岩石断裂的实验观测基础上，建立了岩石穿晶断裂和沿晶与穿晶偶合两个分形模型，并进行了验证，见表 1[9]。岩体块度分布预测与裂隙产生发展的模型在采矿工程中有所应用[22_24]，但这方面仍需大量的基础工作。

岩石表面或断裂面的粗糙度可由分形维定量描述[25_27]，王金安、谢和平等人[28]考察了岩石断裂表面测量时的尺度效应，提出了分形测量的途径。在节理粗糙度方面，谢和平等[11,29_30]讨论了岩石节理粗糙性的分形描述，JRC与分形维数的关系（图5），以及分维对节理抗剪强度、应力状态和节理摩擦角的影响。

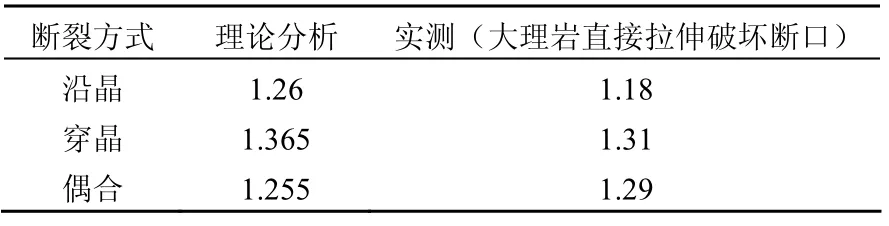
表1 岩石微观断裂的分形维

图5 典型JRC中心值和预测的JRC值与分维之间的关系曲线Fig.5 Relation curve among typical JRC center value,predicted JRC value and fractal dimension.

2.2 渗流分析模型

岩土体是多孔隙介质，其骨架结构和孔隙是分形的，因此流体在这样一个分形空间渗流时，也应当具有分形的特征及其它一些特殊的性质。研究指出，溶质在分形孔隙网络中的扩散并不遵循Fick定律，而是表现为不规则扩散[31]。Yortsos[32]建立了饱和分形介质水份的运输方程，Guerrini和Swartzendruber[33]证明了扩散率随时间而衰减，它们之间是幂律关系，随后建议土中水的运动可用分形布朗运动描述[34]。Yakov[35]和 Dennis在 Yortsos工作的基础上，利用渝渗集团的物理模型，借助质量守恒定律，并假定水力传导系数与含水量及渗流距离相关，得到了土中水的传输方程。

分形模型在模拟岩土材料渗流的问题上取得较大的成功[36_40]，国内外学者模拟岩土体渗流模型的同时，也发展了渗流过程中重要参数求取的分形方法。岩土体的水力参数，是岩土体持水能力、渗透能力等的表征，在岩土工程实践中是极其重要的指标，通常与岩土体强度和稳定性息息相关。岩土体水力性质的分形研究主要集中在渗透系数、土水持水（特征）曲线等方面。非饱和土渗透系数具有很强的饱和度敏感性[41]，其直接测量存在现实的困难，尤其是在低饱和度时，用实验方法直接测量非饱和土的渗透系数几乎不可能，即使测到其精度也有待商榷。土体持水曲线的确定直接关系到非饱和水力传导系数、剪切强度等的确定，是非饱和土工程中极其重要的一环。徐永福等[42]由非饱和土孔隙分布的分形模型导出了非饱和土的土水特征曲线、渗透系数、扩散系数的表达式(式（4）、式（5）、式（6）):

式中ψe为非饱和土的进气值；ψ为非饱和土的基质吸力；Se=(θ−θr)/(θs−θr)，为有效饱和度，θ是非饱和土的体积含水量，θr是残余含水量，θs是饱和含水量；δ=D−3，D是分维。

式中kr是渗透系数;η=3D−11。

式中d是扩散系数;ξ=2D−7;ks是饱和渗透系数。

目前基于岩土体结构的分形特征，利用分形理论求取渗透系数、预测土体特征曲线的方法已渐趋全面和成熟，并在实践中有所应用[15,43_48]。

2.3 岩土材料的强度

节理裂隙的分形发育与分布，岩体自身的分形结构，是构成利用分形理论研究岩体强度的基础。谢卫红、谢和平等[29,49_50]研究了不同分形节理粗糙度在不同加载条件下对岩石力学特性及单轴压缩条件下对应力状态的影响，得出了一些有益的结论。王金安等[51_52]研究了剪切过程中岩石节理粗糙度的分形演化及力学特征，结果表明，仅依据分形维数D不足以确定岩石节理粗糙度与岩石节理力学行为之间的关系，在许多情况下，岩石节理的力学性质对截距的依赖程度大于对分维D的依赖程度。高峰等[53]则认为岩体强度与岩体中节理分布的分形维数密切相关，分形维数增大导致岩体强度非线性降低。在岩石损伤方面，高峰等[54]认为，岩石初始损伤与岩石破碎之间有着较强的相关性，通过分析岩石结构中初始缺陷分布来预测岩石破碎后碎块的尺度分布规律是可能的；徐志斌和谢和平[55]认为，岩石断裂的损伤演化过程具有良好的统计自相似性，损伤演化过程是一个增维的过程。

分形理论在土体强度预测（主要是非饱和土）中的应用，主要通过采用土体孔隙的分形模型，预测土体含水率或土水特征曲线，进而与土体剪切强度相关联[42, 56]:

式中fτ是抗剪强度;c′是有效粘聚力;σ是正应力;ua是孔隙气压;φ′是有效内摩擦角;常数ξ介于0～1.0。

谢学斌和潘长良[57]研究了矿山排土场散体岩石粒度分布的分维规律，结果表明，分维数与散体岩石的剪切强度参数摩擦角呈负指数关系；舒志乐等[58]对不同粒度分维不同围压下土石混合体的应力－应变特性、强度参数特征及峰值强度特征进行分析并讨论它们之间的关系，结果显示，粒度分维值对强度影响很大，而只具一维分形的土石混合体具有最大的密实度和抗剪强度。Bonala等[59]采用土粒分形模型探讨了土体的粘聚力、土体抗剪强度与土体粒度分维的关系。

2.4 分形空间力学特征

传统的力学定律及法则均建立在整数维空间的基础上，而对于分形结构材料，在分数维空间，这些力学定律法则是否成立及是否具有新特征，是一个亟需探讨的问题。

由于分形数学的特殊性，在欧氏空间中无法定义分形空间的力学量及其导数，如位移梯度等等，必须引入分形空间和Besov空间[60_62]。通常情况下，分形物体或者分形结构的物理力学行为呈现分形特征。谢和平等[63]对损伤力学行为在分数维空间中的演化规律进行了初步探讨，推导了材料损伤演化律和损伤本构关系的分形表达形式。

在分数维空间建立描述分形体力学行为的变量和力学定律表达式及运算法则，是分形理论向力学领域深入发展的奠基石，同时也是难点，目前虽有一定量的进展[61,64_67]，但尚未见到这方面系统的成熟的研究成果。

3 结论

自分形理论引入岩土力学领域以来，已经在理论研究和应用研究中取得一系列成果[12,66,68]，比如岩土体孔隙结构的分形描述及强度预测，岩石裂纹扩展机制、损伤力学及能量耗散的分形研究，地震力学中的分形特征，分形熵与热力学、开矿工程的岩爆预测等等。然而，当前的研究只是起步，分形理论应当继续深入到岩土力学中的各个领域，继续深化与创新。只有将分形理论引入现有的力学框架，更广泛探索分数维空间各种力学的力学量、演化规律及本构模型，理清岩土力学系统各种基本原理和方法在欧氏空间和分形空间的关系，才能产生对岩土材料非线性力学行为的新认识，推动岩土材料细观力学、微观力学、宏观力学理论和应用的综合发展。

[1]谢和平. 分形几何及其在岩土力学中的应用[J]. 岩土工程学报,1992, 14(1): 14-24.

[2]Mandelbrot B B. Fractals: from, chance and dimension[M].San Francisco: W.H. Freeman, 1977.

[3]Mandelbrot B B. The Fractal Geometry of Nature[M]. San Francisco:W.H. Freeman, 1982.

[4]毛灵涛, 薛茹, 袁则循. 软土路基微结构扫描电镜图像的分形[J].长安大学学报（自然科学版）, 2007, 27(2): 30-33.

[5]陈颙，陈凌. 分形几何学（第2版）[M]. 北京：地震出版社, 2005.[6]孙博玲. 分形维数(Fractal dimension)及其测量方法[J]. 东北林业大学学报, 2004, 32(3): 116-119.

[7]Fredlund D G, Rahardjo H. Soil Mechanics for Unsaturated Soils [M].New York: John Wiley & Sons, 1993.

[8]Friesen W I, Mikula R J. Fractal dimensions of coal particles[J].Colloid Interf., 1987,120:263-271.

[9]XIE He－ping, Chen Zhi－da. Fractal Geometry and Fracture of Rock[J]. Acta Mechanica Sinica, 1988, 4(3):255-264.

[10]谢和平. 岩土介质的分形孔隙和分形粒子[J]. 力学进展, 1993,23(2): 145-164.

[11]谢和平. 岩石节理的分形描述[J]. 岩土工程学报, 1994, 17(1):18-23.

[12]XIE He-ping. Fractals in Rock Mechanics[M]. Rotterdam: A.A.Balkema Publisher, 1993.

[13]Tyler S W, Wheatcraft S W. Fractal scaling of soil particle－size distributions: analysis and limitations[J]. Soil Science Society of America, 1992, 56(1): 362-369.

[14]Crawford J W, Sleeman B D, Young I M. On the relation between number－size distributions and the fractal dimensions of aggregates[J].Journal of Soil Science, 1993, 44:555-565.

[15]XU Yongfu, SUN De’an. A fractal model for soil pores and its application to determination of water permeability[J]. Physica A:Statistical Mechanics and its Application, 2002, 316(1-4): 56-64.

[16]Mandelbrot B B. The Fractal Geometry of Nature[M]. New York,W.H.Freeman and company, 1982.

[17]Turcotte D L. Fractals and fragmentation[J]. Journal of Geophysical Research, 1986, 91(B2):1921-1926.

[18]Crawford J W, Matsui N, Young I M. The relation between the moisture release curve and the structure of soil[J]. European journal of soil science, 1995, 46(3): 369-375.

[19]Avnir D, Farin D, Pfeifer P. Surface geometric irregularity of particulate materials: the fractal approach[J]. Journal of Colloid Interface Science, 1985, 103: 112-123.

[20]涂新斌, 王思敬, 岳中琦. 风化岩石的破碎分形及其工程地质意义[J]. 岩石力学与工程学报, 2005, 24(4): 587-595.

[21]刘晓明, 赵明华, 苏永华. 沉积岩土粒度分布分形模型改进及应用[J]. 岩石力学与工程学报, 2006, 25(8): 1691-1697.

[22]XIE H-ping. Fractal Characteristic in Geological Material Mechanics[J]. In: Applied Mechanics, Int. Academic Publishers,Pergamon Press, 1989: 1255-1260.

[23]谢和平, 于广明, 杨伦, 等. 采动岩体分形裂隙网络研究[J]. 岩石力学与工程学报, 1999, 18(2): 147-151.

[24]王利, 高谦. 基于损伤能量耗散的岩体块度分布预测[J]. 岩石力学与工程学报, 2007, 26(6): 1202-1211.

[25]WANG Jin-an, XIE He-ping. Fractal properties of rock fracture surfaces[J]. Journal of Coal Science and Engineering, 1996, 2(1):16-23.

[26]王金安, 谢和平. 岩石断裂面的各向异性分形和多重分形研究[J].岩土工程学报, 1998, 20(6): 16-21.

[27]孙洪泉, 谢和平. 岩石断裂表面的分形模拟[J]. 岩土力学, 2008,29(2): 347－352.

[28]王金安, 谢和平, 田晓燕, 等. 岩石断裂表面分形测量的尺度效应[J]. 岩石力学与工程学报, 2000, 19(1): 11-17.

[29]谢卫红, 谢和平, 赵鹏. 分形节理粗糙度对应力状态影响的研究[J].岩石力学与工程学报, 1998, 17(3): 253-258.

[30]谢和平, 王金安. 岩石节理（断裂）表面的多重分形性质[J]. 力学学报, 1998, 30(3): 314-320.

[31]Gefen Y, Aharony A, Alexander S. Anomalous diffusion on percolating clusters[J]. Physical Review Letters, 1983, 50(1): 77-80.

[32]Yortsos Y C. Heterogeneity description using fractal concepts[J].Modeling and applications of transport phenomena in porous media.Rhode Saits Genese, Von Karman Institute for Fluid Dynamics, 1990,1: 1-35.

[33]Guerrini I A, Swartzendruber D. Soil water diffusivity as explicitly dependent on both time and water content[J]. Soil Science Society of America, 1992, 56(1): 335-340.

[34]Guerrini I A, Swartzendruber D. Fractal characteristics of the horizontal movement of water in soils[J]. Fractals, 1994, 2(3):465-468.

[35]Yakov P, Dennis T. Water transport in soils as in fractal media[J].Journal of Hydrology, 1998, 204: 98-107.

[36]Thevanayagam S, Nesarajah S. Fractal Model for Flow Through Saturated Soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(1): 53-66.

[37]周宏伟, 谢和平. 岩体中渗流形貌演化的随机理论描述[J]. 岩土工程学报, 2001, 23(2): 183-186.

[38]LI Shou-ju, LIU Ying-xi. Application of Fractal Models to Water and Solute Transport in Unsaturated Soils[J]. Advances in Unsaturated Soil, Seepage, and Environmental Geotechnics, 2006, (148): 195-202.

[39]褚卫江, 徐卫亚. 分形介质饱和渗流应力耦合数值模拟研究[J]. 岩石力学与工程学报, 2007, 26(S1): 2641-2647.

[40]任强, 徐卫亚. 裂隙岩体非饱和渗流的分形模型[J]. 岩土力学,2008, 29(10): 2735-3740.

[41]Jarvis N J, Messing I. Near－saturated hydraulic conductivity in soils of contrasting texture as measured by tension infiltrometers[J]. Soil Science Society of America Journal, 1995, 59(1): 27-34.

[42]徐永福, 黄寅春. 分形理论在研究非饱和土力学性质中的应用[J].岩土工程学报, 2006, 28(5): 635-638.

[43]徐永福, 董平. 非饱和土的水分特征曲线的分形模型[J]. 岩土力学,2002, 23(4): 400-405.

[44]孙大松, 刘鹏, 夏小和. 非饱和土的渗透系数[J]. 水利学报, 2004,(3): 71-75.

[45]HUANG Guan-hua, ZHANG Ren-duo. Evaluation of Soil Water Retention Curve with the Pore－Solid Fractal Model[J]. Geoderma,2005, (127): 52-61.

[46]HUANG Guan-hua, ZHANG Ren-duo, HUANG Quan-zhong.Modeling Soil Water Retention Curve with a Fractal Method[J]. Soil Science Society of China, 2006, 16(2): 137-146.

[47]CHEN Jing-yu, GONG Xiao-nan, WANG Ming-yuan. A Fractal－Based Soil－Water Characteristic Curve Model for Unsaturated Soils[J]. Advances in Unsaturated Soil, Seepage, and Environmental Geotechnics, 2006, (148): 55-61.

[48]Soto M A, Vilar O M. Evaluation of a Pore Fractal Model for the Prediction of Soil Water Retention Curve[C]. International Conference on Unsaturated Soils, Carefree, AZ(US) , 2006: 2441-2452.

[49]谢卫红, 谢和平, 李世平, 等. 分形节理力学性能试验研究[J]. 工程力学, 1997, 14(4): 128-138.

[50]谢卫红, 谢和平, 李世平, 等. 分形节理的强度和变形研究[J]. 长春地质学院学报, 1997, 27(3): 284-288.

[51]王金安, 谢和平, Kwasniewski M A. 剪切过程中岩石节理粗糙度分形演化及力学特征[J]. 岩土工程学报, 1997, 19(4): 2-9.

[52]王金安, 谢和平, Kwasniewski M A. 岩石节理面在剪切中表面损伤的分形演化[J]. 力学与实践, 1997, 19(4): 56-58.

[53]高峰, 钟卫平, 黎立云, 等. 节理岩体强度的分形统计分析[J]. 岩石力学与工程学报, 2004, 23(21): 3608-3612.

[54]高峰, 谢和平, 巫静波. 岩石损伤和破碎相关性的分形分析[J]. 岩石力学与工程学报, 1999, 18(5): 503-506.

[55]徐志斌, 谢和平. 断裂尺度的分形分布与其损伤演化的关系[J]. 地质力学学报, 2004, 10(3): 268-275.

[56]XU Y F. Fractal Approach to Unsaturated Shear Strength[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(3):264-273.

[57]谢学斌, 潘长良. 排土场散体岩石粒度分布与剪切强度的分形特征[J]. 岩土力学, 2004, 25(2): 287-291.

[58]舒志乐, 刘新荣, 刘保县, 等. 基于分形理论的土石混合体强度特征研究[J]. 岩石力学与工程学报, 2009, 28(S1): 2651-2656.

[59]Bonala M V S, Reddi L N. Fractal Representation of Soil Cohesion[J].Journal of Geotechnical and Geoenvironmental Engineering, 1999,125(10): 901-904.

[60]Panagiotopoulos P D, Panagouli O K, Mistakidis E S. Fractal geometry and fractal material behavior in solids and structure[J].Archive of Applied Mechanics, 1993, 63(1): 1-24.

[61]谢和平. 分形力学的数学基础[J]. 力学进展, 1995, 25(2): 174-185.[62]谢和平. 分形力学研究进展[J]. 力学与实践, 1996, 18(2): 10-18.

[63]谢和平, 鞠杨. 分数维空间中的损伤力学研究初探[J]. 力学学报,1999, 31(3): 300-310.

[64]苏维宜. Fractal 空间[C].全国第二次分形学术讨论会论文集. 武汉,1991.

[65]苏维宜. Fractal与导数[R]. 全国第二次分形学术讨论会特邀报告.武汉, 1991.

[66]谢和平. 分形－岩石力学导论[M]. 北京: 科学出版社, 1997.

[67]谢和平, 薛秀谦. 分形应用中的数学基础与方法[M]. 北京: 科学出版社, 1997.

[68]XIE He-ping, Parisean W G. Fractal estimation of joint roughness coefficients[J]. Science in China(Series B), 1994, 37(12): 1516-1524.