工件检测中基于方向码的图像模板匹配

黄 静， 蔡雪艳 ， 于 娜

（1.石家庄铁路运输学校 河北 石家庄 050030；2.石家庄计算机职业学院 河北 石家庄 050300；3.中国联通沧州分公司 河北 沧州 061000）

近年来基于机器视觉检测技术成为一种新兴的应用学科，被越来越多地应用到在线检测中，实现高度准确的检测，大幅提高产品检测的速度和可靠性，降低了生产成本。工件检测系统主要是通过在线工件和模板工件进行比较，最终对工件进行合格品与非合格品的分选处理[1]。

模板匹配主要分为两种：一是基于灰度的模板匹配；二是基于特征的模板匹配。基于灰度的模板匹配方法速度比较慢，对光照变化、噪声非常敏感，没有充分利用灰度统计特性，对每一点的灰度信息依赖较大，不适合应用于匹配对象存在旋转和缩放的情况。基于特征的模板匹配算法一般不直接依赖于像素值，并且需要经过较为复杂的图像预处理以提取特征，通常在模板和待匹配图像中提取对缩放、旋转、灰度变化具有不变性的特征。

对于在流水线上运动的工件来说，它们的位置和角度不是固定的，工作环境的光照也是变化的，所以要求提取的特征应当具有旋转平移不变性和对光照强度的鲁棒性。本文在研究前人工作的基础上，针对工件在线检测的现场环境，提出了以方向码为特征的图像模板匹配，该算法不仅能抗旋转，而且在遮挡和光强引起的光照波动等情况下，也能较好地进行匹配。

1 图像预处理

图像的预处理包括对原始图像进行灰度变化，滤波、归一化、特征提取、分割等匹配之前的处理。主要目的是消除图像中的无关信息，恢复有用的真实信息，增强有关信息的可检测性，最大限度地简化数据。

1.1 灰度变化

灰度变换指根据某种目标条件按一定变换关系逐点改变原图像中每一个像素灰度值的方法。目的是为改善画质，使图像的显示效果更加清晰。图1所示为拉伸前后的对比图像。

图1 灰度拉伸效果Fig.1 Effect of gray stretching

设原图像的灰度值D=f（x，y），处理后图像像素的灰度值D′=g（x，y），则灰度增强可表示为：

经过灰度变换后，像素动态范围增加，图像的对比度扩展，使图像变得更加清晰、细腻，容易识别。

1.2 中值滤波

中值滤波是一种非线性处理的方法，它的基本原理是把数字图像或数字序列中的一点的值用该点的一个领域中的各点的中值代替[2]。中值的定义如下：

一组数x1，x2……xn，把n个数按值的大小顺序排列如下：

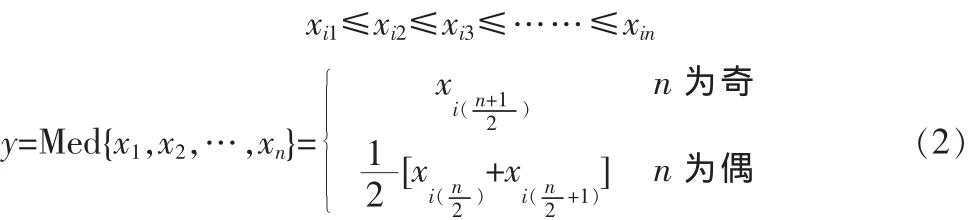
中值滤波能很好的保留边界，对滤除脉冲噪声，线性噪声，孤立点都很有效。本文采用3×3滤波。

图2 中值滤波效果Fig.2 Effect of median filtering

2 匹配原理

模板匹配的基本思想是：首先获取各待分类的标准产品图像，以建立对应的标准图像模板。然后，分别将这些标准图像模板在实时采集的图像上做平移和旋转，同时进行相关性计算，若最大的相关值大于设定的阈值，则可认为在实时图像中存在该标准模板所代表的产品。

本文提取方向码作为特征，整个匹配过程分为粗匹配和精匹配两个步骤。匹配流程如图3所示。首先将模板和待匹配图像进行预处理，计算出模板和模板覆盖下子图的方向码，得到模板和子图的方向码直方图，移动子图方向码直方图，每移动一次计算模板和子图方向码直方图的相似面积。即以它们在每个方向上的方向码频率值作竖坐标，每个方向作为横坐标，做柱状图，求子图和模板在每个方向上的频率值的公共部分所包含的面积A，作为其相似性度量，得到相似矩阵S1，当A取最大值时依据直方图的移动次数l估算得出子图相对于模板旋转的角度α。如果A大于预定阈值，则记下子图的位置以便在此位置进行精匹配阶段。在每一个匹配候选点上，根据第一步得到的旋转角度旋转模板，得到旋转后的方向码，再计算模板和子图的相似性，得到相似性矩阵S2，综合S1和S2得到最佳匹配点。

图3 匹配流程Fig.3 Matching process

2.1 方向码的定义

将[0，2π]范围等分成 N个区间，N选为 16，则每个区间的角度Δθ是π/8，从水平方向开始就按逆时针方向依次给每个区间赋予一个序号，这个序号就是方向码值，如图4所示[3]。

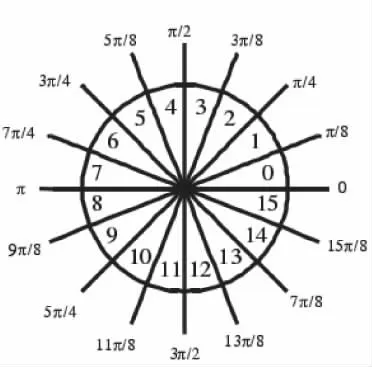
图4 方向码Fig.4 Direction code

为了得到图像的方向码，必须先计算出每个像素点的梯度角。本文Δ采用sobel差分Δ算子来计算梯度角，得到像素点的水平差分Δ fΔx和垂直差分 fy后，位置（i，j）处的梯度角 θ（i，j）=arctan（fy/fx），方向码 c（i，j）定义为

[.]——去整运算，Γ——阈值。

如果方向码有 N 个，c（i，j）就在集合{0，1，2，……N－1}中取值。阈值Γ的选取一般视具体情况而定，过大，就会忽略到有用的梯度，过小，噪声的影响就会变大。在本文的实验中选10。选择sobel算子计算梯度角原因有二：1）由于引用了平均因素，因而对图像的随机噪声有平滑作用。2）由于它是相隔两行或两列之差分，故边缘两侧得到增强，边缘显得粗而亮[4]。图5为robert和sobel效果比较图。

图5 robert和sobel效果比较Fig.5 Comparison between Robert and Sobel

2.2 工件定位

图像经过sobel算子检测之后，便要对图像进行扫描，以确定工件区域的确切置。定位方法都是直接或间接的分析工件的纹理特征。所谓的纹理特征就是扫描图像得到的灰度变化曲线。在一幅图像中工件的纹理特征很明显的区别于背景，有自己的变化特征。为了便于分析，需要对整个图像二值化，得到只含有0和1的灰度图，根据实验结果对工件图像二值化的阈值选择210。二值化后结果如图6所示。

图6 sobel算子检测后二值化图像Fig.6 Binarized image using sobel operator

然后利用投影法把图像在水平方向和垂直方向上进行投影[5]。在投影图上便可反映出图像中目标对象的位置、尺寸等信息。至此确定出待匹配工件的在图像中的确切位置。为后来的模板匹配缩小了范围，大大减少了计算量，提高了检测速度。图7是一幅图像分别在水平方向和垂直方向上的投影。

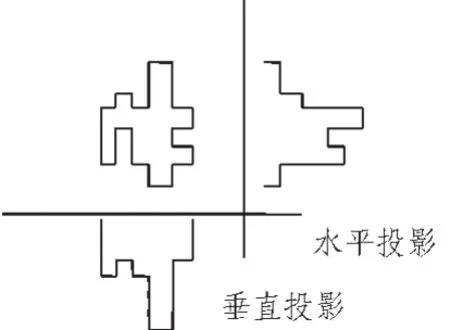
图7 投影法Fig.7 Projection method

2.3 粗匹配

模板方向码直方图表达式为：

位置（i，j）处的子图为 fij的方向码直方图为：

子图直方图中的第k个区域用下式表示[3]：

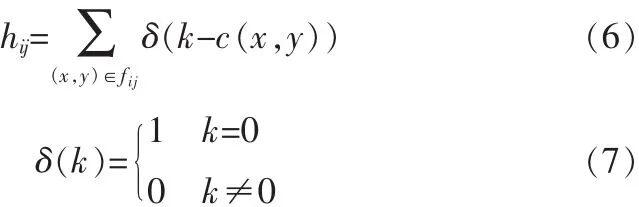
要在每一点计算灰度梯度方向角，在每一子图中统计方向码的直方图，最后通过遍历移位比较相似性。

本文采用模板和子图直方图的绝对差来度量两个直方图之间的相似性，用 s1（x，y）来表示[6]。

式中，l表示模板方向码直方图右移次数，取值{0，1，2……N－1}，sl表示右移l次后子图和模板方向码直方图的交集面积。

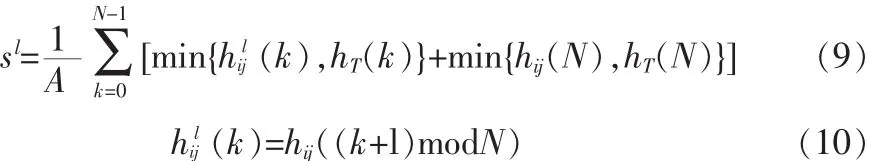
其中，A是模板像素个数。在本文中把s1（x，y）＞0.9的点作为匹配候选点，根据此时子图直方图移动次数计算出子图相对于模板旋转的角度 α，α=移动直方图时，方向码为N的区域不移动。

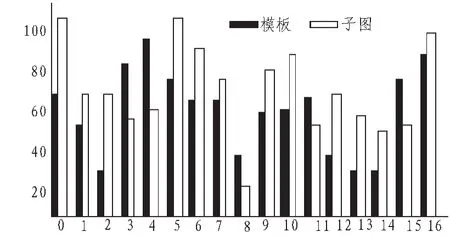
图8 方向码直方图Fig.8 Histogram of direction codes

2.4 精匹配

由上面的直方图匹配可以得出匹配候选点，和子图相对于模板的旋转角度。根据旋转角度将模板进行旋转，得到旋转后模板的方向码图像。用OT表示模板的方向码图像，Oxy表示左上角坐标为（x，y）的子图方向码图像，则模板和子图间的相似性 s2（x，y）为：

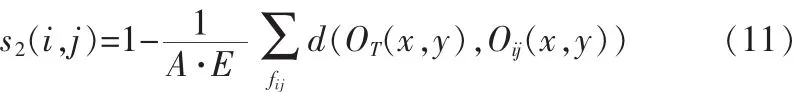
方向码间的差值为：

E是任意两个方向码的最大差值，所以E=N/2。

2.5 最佳匹配点

经粗匹配和精匹配步骤，得到两个相似度量值的矩阵S1和S2，求两个同一点的两个相似度量值的平均值，得到这一点的总的相似度量值S。取最大的S值处的像素点为最佳匹配点[7]。

3 实验结果

为了验证该匹配算法的准确程度，进行了实验。首先将工件旋转到标准方向，进行模板创建。然后将工件逆时针旋转30°，45°，60°，90°，并且伴以亮度变化，可以得到结果如表 1 所示。

表1 实验结果Tab.1 Experimental results

实验表明，该算法可以成功的对工件进行匹配，而且可以估算出工件的旋转角度。

4 结束语

通过前面的讨论和实验数据可以看出，本文提出的结合工件检测实际环境的基于方向码的模板匹配有以下特点：1）在匹配识别上不仅不受物体方位旋转及尺寸缩放变化影响，而且能较精确地求出物体相对与模板的偏转角度；2）对待检测图像先进行工件定位，确定工件的大体位置，这样大大提高了检测速度。

[1]何东健，耿楠，张义宽.数字图像处理[M].西安:西安电子科技大学出版社，2003.

[2]吕景亮.工件检测中图像处理算法研究[D].长春:长春理工大学，2004.

[3]Ullah F，Kaneko S，Igarahi S.Object search using orientation histogram intersection[C]//Proceedings of Japan-Korea Joint Workshop on Frontiers of Computer Vision，Seoul，2000：110-115.

[4]刑军.基于sobel算子数字图像的边缘检测算法[J].微机发展，2005，15（9）:48-52.XING Jun.Edge detection of Sobel based digital image[J].Microcomputer Development， 2005，15（9）:48-52.

[5]刘锦峰.图像模板匹配快速算法研究[D].长沙:中南大学，2007.

[6]段德山.工件非接触检测中机器视觉的研究与应用[D].北京:北京邮电大学，2007.

[7]王强，宋京民，胡建平.一种快速模板匹配目标识别算法[J].计算机工程及应用，2000，36（6）:30-32.WANG Qiang， SONG Jing-min， HU Jian-ping.An improved template matching algorithm of target recognition[J].Computer Engineering and Applications， 2000， 36（6）:30-32.