用SAS软件实现单因素多水平设计定量资料的统计分析

胡良平,吕辰龙 (军事医学科学院科技部生物医学统计学咨询中心,北京100850)

上期介绍了成组设计定量资料的一般处理方法,试验中仅涉及一个具有两水平的试验因素,例如,研究某种药物对不同性别、同种疾病病人的治疗效果,试验因素即为性别。但在有些试验中,试验因素涉及的水平数可能超过两个,例如希望比较三种药物对某种疾病治疗效果的优劣,或者比较某种药物对同种疾病三种不同类型的治疗效果。对于第一种情况,最合适的方法就是选择患了该病但病情和其他重要非试验因素方面(如病程、病型、病人的基础健康状况等)相近的病人若干,将他们随机分成三组,分别接受不同药物治疗,观测一项或多项指标来衡量最终的治疗效果,这时所运用的试验设计方法即为单因素三水平设计。下面看一个例子。

例1 为探讨褪黑素对脂肪组织代谢的影响,将24只 SD大鼠随机分为正常对照组(灌服含2%乙醇的生理盐水)、高剂量褪黑素组(10 mg·kg-1·d-1)、低 剂 量 褪 黑 素 组(0.2 m g·kg-1·d-1),每组各8只,干预组每日灌服不同剂量褪黑素溶液,3周后各组大鼠血浆中胰岛素的浓度变化见表1[1]。

上面的例子在科研中经常会遇到,即考察不同剂量同种药物对某些生理指标的影响,选取某种受试对象用该种药物不同剂量分别作用相同时间,分析这段时间后各组之间某观测指标是否存在差异,从而推断出这种药物对生物机理的影响程度。分析三组定量数据样本均值之间的差异是否具有统计学意义,可采用单因素三水平设计定量资料假设检验方法进行统计分析。

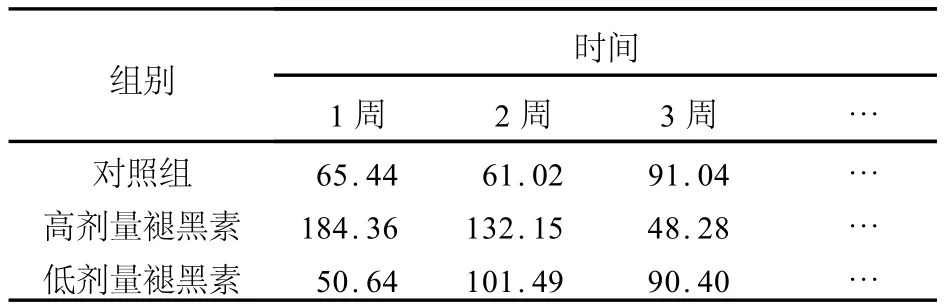
表1 褪黑素治疗后各组大鼠血浆胰岛素浓度的变化aTable 1 Changes of insulin concentrationsafter melatonin treatment in different rat groups (n=8,z B/U·L-1)

1 单因素多水平设计

1.1 单因素多水平设计的定义和特点 试验中涉及一个具有k水平(k≥3)的试验因素,若试验因素独立于受试对象,则可将全部受试对象完全随机地分入该试验的k个水平组中去;反之,将从特定的k个子总体中随机抽取受试对象。观测各组受试对象接受不同处理后,某个或某些定量观测指标的数值,这样安排试验的方法叫做单因素k水平(k≥3)设计或单因素多水平设计。单因素多水平设计的特点是,试验中仅涉及一个具有k水平的试验因素,未对其他任何重要非试验因素进行有计划的安排,仅希望通过随机化分组来平衡所有非试验因素在各组间对观测结果的干扰和影响。在单因素k水平设计中,若定量指标只有1个,则定量资料就叫做单因素k水平设计一元定量资料;若定量指标有m(m＞1)个,则定量资料就叫做单因素k水平设计m元定量资料。1.2 单因素多水平设计定量资料统计分析方法合理选用 (1)试验仅受一个因素影响,并且该因素包含的水平数不小于3,所有观测指标均为定量数据; (2)检测各组定量资料是否同时满足正态性,检测多组定量资料是否满足方差齐性,若满足则采用参数检验(单因素多水平设计一元定量资料方差分析),反之,则采用非参数检验(一元定量资料 Kruskal-Wallis秩和检验);(3)当观测的定量指标为多个时,需采用单因素多水平设计多元方差分析。

2 实例解析

2.1 应用SAS软件分析单因素多水平设计一元定量资料 例2 沿用例1中的资料,试问三组受试对象胰岛素的浓度变化差异有没有统计学意义?

对问题的分析与SAS实现 此资料涉及三组大鼠,试验因素为褪黑素剂量,具有三个水平,分别为“对照组(零剂量组)”、“高剂量褪黑素组”、“低剂量褪黑素组”,观测结果中只有一个定量指标“胰岛素浓度变化”,假定随机分组的方法已经消除或降低了各种非试验因素对观测结果的影响(否则,应按重要非试验因素进行分层随机化),故此定量资料属于单因素三水平设计一元定量资料。对三组大鼠血浆浓度变化分别进行正态性检验,若都服从正态分布,再进一步验证三组试验数据是否满足方差齐性,若观测结果同时满足正态性和方差齐性,可采用单因素三水平设计一元定量资料的方差分析;若有一个条件不满足,可采用 Kruskal-Wallis秩和检验。应用SAS进行分析,程序如下。

程序说明:第1步创建数据集,“group”表示分组因素,“1”是对照组,“2”是高剂量褪黑素组,“3”是低剂量褪黑素组;第3步调用UN IVARIA TE过程,对观测结果进行正态性检验;第4步调用GLM过程对观测结果进行方差齐性检验和参数检验,并利用SN K法进行两两比较,若观测结果同时满足正态性和方差齐性,则查看此部分的结果,若有一个条件不满足,则查看第5步非参数检验的结果。SAS输出结果及结果解释:第3步部分输出结果:

/＊第1步.创建数据集＊/ data new; input group; do i=1 to 8; input x@@; output; end; cards; 1 65.44 61.02 91.0 17.97 105.63 88.24 31.97 40.47 2 184.36 132.15 48.28 99.88 77.99 7.84 14.03 29.62 3 50.64 101.49 90.40 42.37 119.94 45.20 21.18 43.29 ; run; /＊第2步.按组别进行排序＊/ p roc so rt; by group; run; /＊第3步.正态性检验＊/ p roc univariate normal noprint; var x; by group; output out=AA normal= w p robn=p; run; /＊网页格式输出结果＊/ ods html; p roc p rint data=AA noobs; var group w p; run; /＊第4步.方差齐性检验和方差分析＊/ p roc glm data=new; class group; model x=group/ss3; means group/hovtest snk; run; quit; /＊第5步.非参数检验＊/ p roc npar1way data=new wilcoxon; class group; var x; run; ods htm l close; quit;

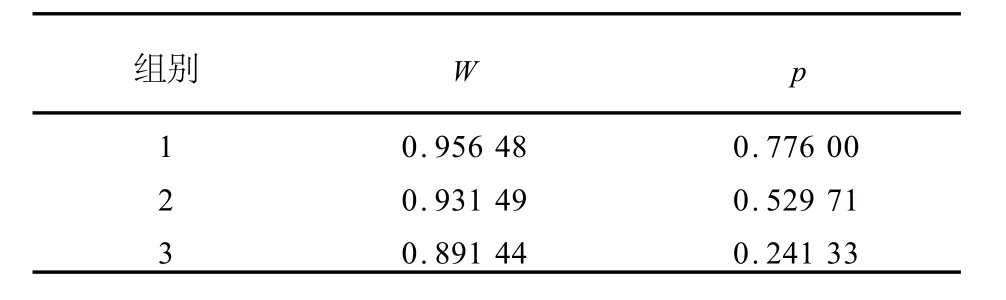
SAS系统正态性检验Test of normality of SAS system

从结果可以看到,三组数据正态性检验的 P值均＞0.05,满足正态性要求。

第4步部分输出结果:

GLM过程The GLM procedure对变量x采用Levene法进行方差齐性检验各组偏差平方的方差分析Levene’s test for homogenety of x variance ANOVA of squared deviations from group means

该部分给出的是方差齐性的检验结果,F值为2.80,P值为0.083 8＞0.05,说明该定量资料满足方差齐性要求。综上可知,需要查看参数检验的结果,也就是GLM过程的输出结果。

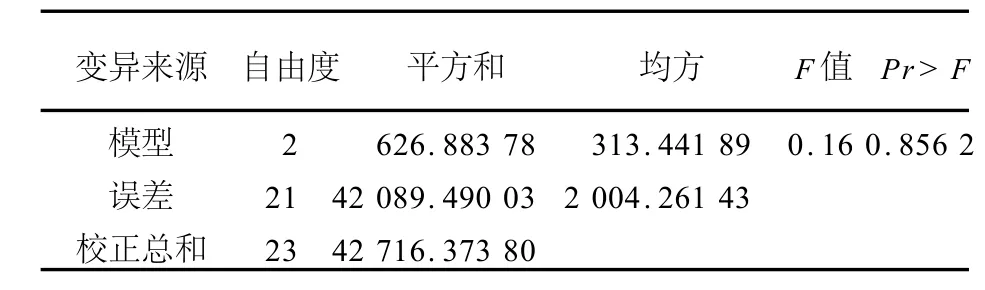
GLM过程The GLM procedure因变量:xDependen t Variable:x

该部分给出的是差异性的统计分析结果,可以看到,F值为0.16,P值为0.856 2＞0.05,因此认为三组数据之间没有统计学差异。

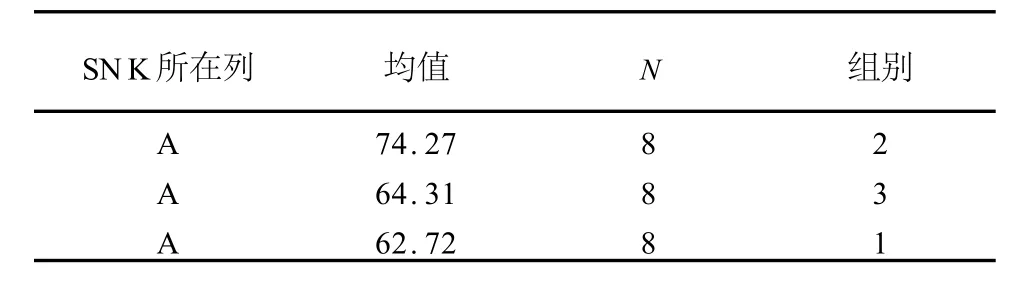
具有相同字母的任何两个平均值之间的差异无统计学意义Means with the same letter are not significantly different

这部分给出的是两两比较的结果,从这里也可以得到三个平均值之间的差别无统计学意义的结论,因为三组数据同属于A类(观察SN K所在列)。

第5步部分输出结果:

Kruskal-Wallis秩和检验Kruskal-Wallis test

这部分给出的是非参数检验的结果,如果观测数据不满足参数检验的前提条件,需要查看此部分的输出结果。由上面的输出结果可以得到χ2= 0.02,P值为0.99。

统计学和专业结论:F值为0.16,P值为0.856 2＞0.05,故按α=0.05水准,认为三组大鼠血浆胰岛素浓度变化之间的差异无统计学意义。即不同的褪黑素剂量对大鼠血浆胰岛素浓度变化的影响程度基本相同。

2.2 应用SAS软件分析单因素多水平设计多元定量资料 上面给出的是单因素多水平一元定量资料的例子,如果观测结果涉及到在专业上有一定联系的多个定量指标时,则需要采用多元方差分析方法处理,联合考察多个定量指标在组间的整体差异(在统计学上称为均值向量之间的比较)是否具有统计学意义,由此得出基于多个定量指标整体评价的统计学和专业结论。

例3 继续沿用例1的试验设计,观测指标和结果见表2[1],请作统计分析。

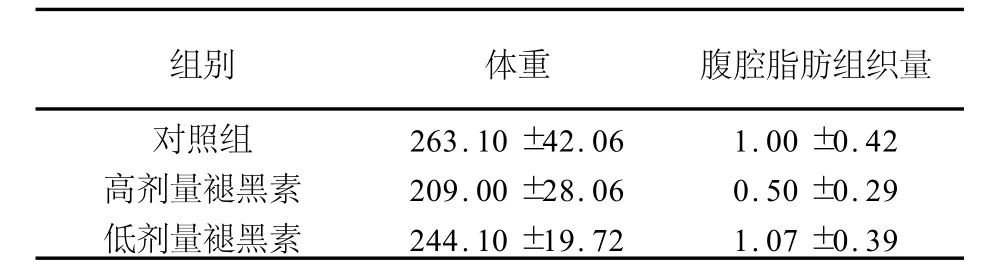
表2 褪黑素治疗3周后各组大鼠体重及腹腔组织量的变化aTable 2 Changes of body weight and mass of intra-abdom inal fat after melatonin treatment for3 weeks in different rat groups (n=8,m/g)

对问题的分析与SAS实现 此例观测的指标是两个定量指标,分别为体重和腹腔脂肪组织量,试验因素仍是褪黑素剂量,具有三个水平,属于单因素三水平设计二元定量资料,采用单因素三水平设计定量资料二元方差分析[2]。假设三组数据均满足参数检验的前提条件,实现此分析的SAS程序如下:

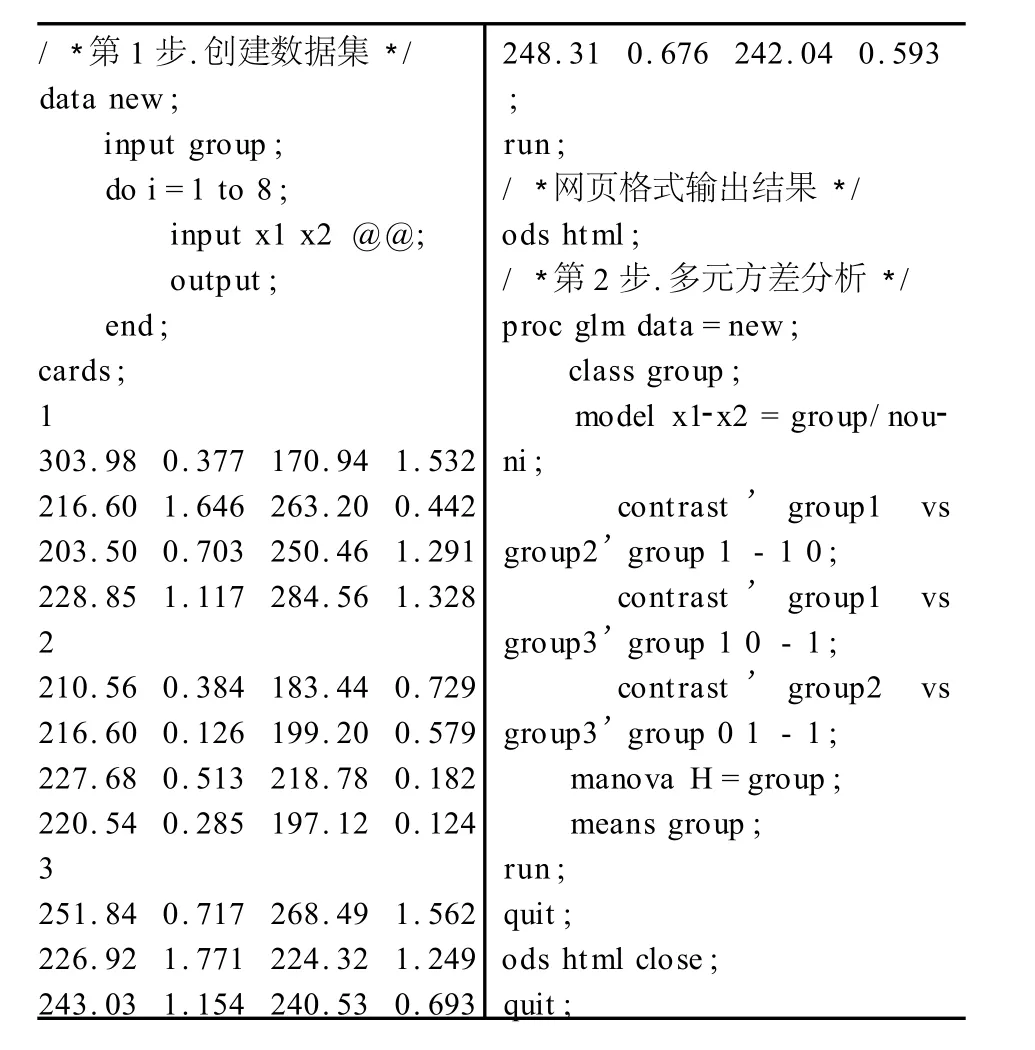
/＊第1步.创建数据集＊/ data new; input group; do i=1 to 8; input x1 x2@@; output; end; cards; 1 303.98 0.377 170.94 1.532 216.60 1.646 263.20 0.442 203.50 0.703 250.46 1.291 228.85 1.117 284.56 1.328 2 210.56 0.384 183.44 0.729 216.60 0.126 199.20 0.579 227.68 0.513 218.78 0.182 220.54 0.285 197.12 0.124 3 251.84 0.717 268.49 1.562 226.92 1.771 224.32 1.249 243.03 1.154 240.53 0.693 248.31 0.676 242.04 0.593 ; run; /＊网页格式输出结果＊/ ods htm l; /＊第2步.多元方差分析＊/ p roc glm data=new; class group; model x1-x2=group/nouni; contrast’group1 vs group2’group 1-1 0; contrast’group1 vs group3’group 1 0-1; contrast’group2 vs group3’group 0 1-1; manova H=group; means group; run; quit; ods htm l close; quit;

程序说明:第二步调用 GLM过程做多元方差分析,nouni表示只做多元方差分析不做一元方差分析,manova H=group是启动多元方差分析的选项;contrast表示对三组数据之间进行两两比较,将对比的两个水平中的一个用“1”表示,另一个用“-1”表示。

SAS输出结果及结果解释:

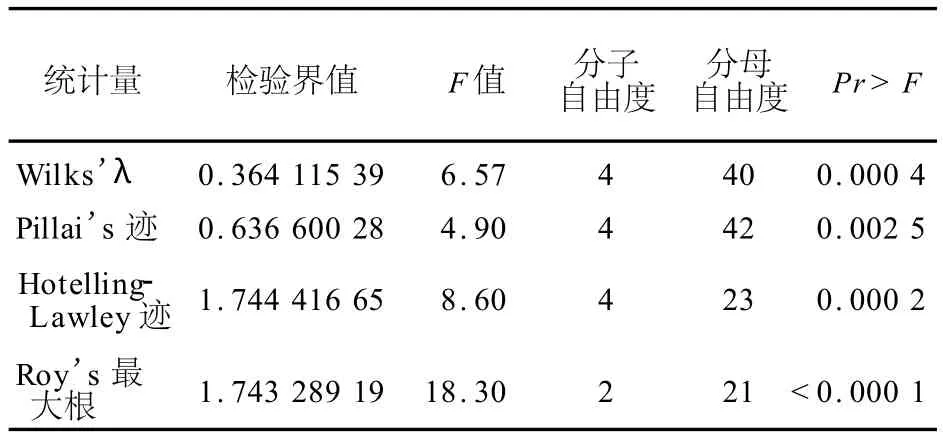
对于没有组间效应的假设所做的多元方差分析的检验界值和近似F值H=组间III型离差矩阵,E=误差离差矩阵M ANOVA test criteria and F approximations for the hypothesis of no overall group effect H=type IIISSCPmatrix for group E=error SSCPmatrix S=2 M=-0.5 N=9

这步给出的是多元方差分析的输出结果,通常只用第一行上的计算结果。故仅关注 Wilks’Lambda统计量,其对应的 F值为 6.57,P值为0.000 4＜0.05,说明就三项定量指标整体而言,三组之间的差异有统计学意义。

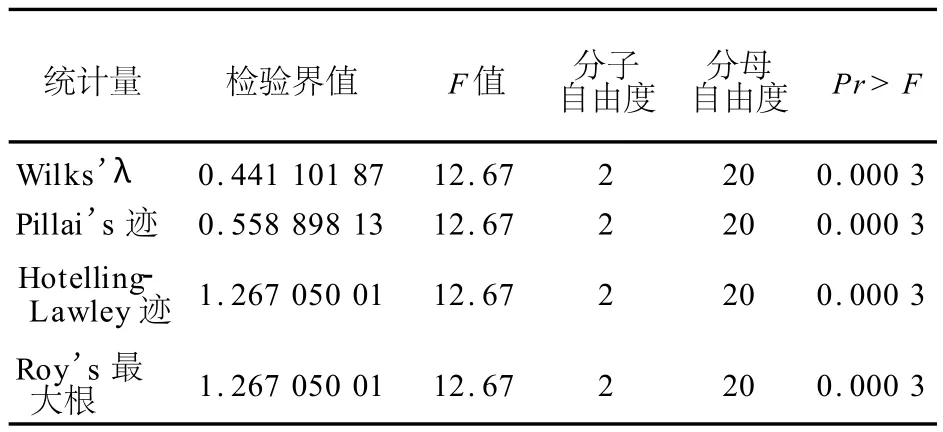
对于没有第一组与第二组组间效应的假设所做的多元方差分析的检验界值和近似 F值H=第一组与第二组组间比较离差矩阵E=误差离差矩阵MANOVA test criteria and exact F statistics for the hypothesis of no overall group 1 vs group 2 effect H=contrast SSCPmatrix for group 1 vs group 2 E=error SSCPmatrix S=1 M=0 N=9

这三部分给出的是三组之间两两比较的结果,通过观察W ilks’Lambda统计量,得到第1组与第2组之间差异有统计学意义(F=12.67、P= 0.000 3＜0.05),第2组与第3组之间差异有统计学意义(F=13.47、P=0.000 2＜0.05),第1组与第3组之间差异没有统计学意义(F=0.02、P= 0.976 7＞0.05)。

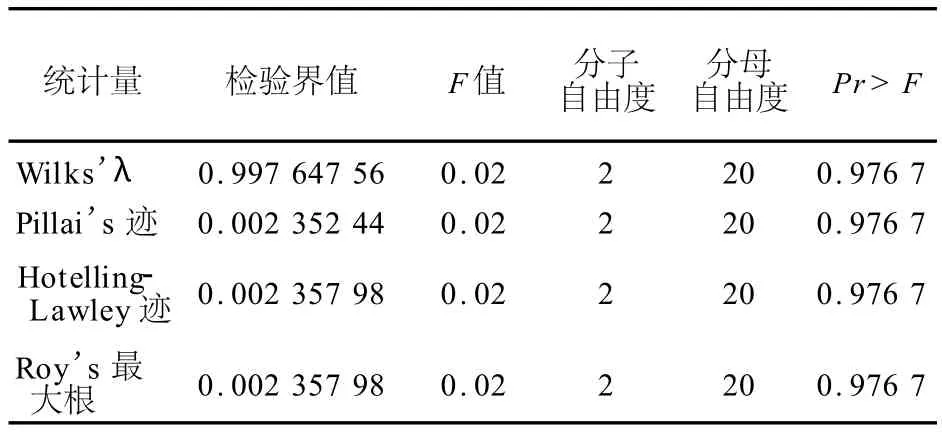
对于没有第一组与第三组组间效应的假设所做的多元方差分析的检验界值和近似 F值H=第一组与第三组组间比较离差矩阵E=误差离差矩阵MANOVA test criteria and exact F statistics for the hypothesis of no overall group 1 vs group 3 effect H=contrast SSCPmatrix for group 1 vs group 3 E=error SSCPmatrix S=1 M=0 N=9

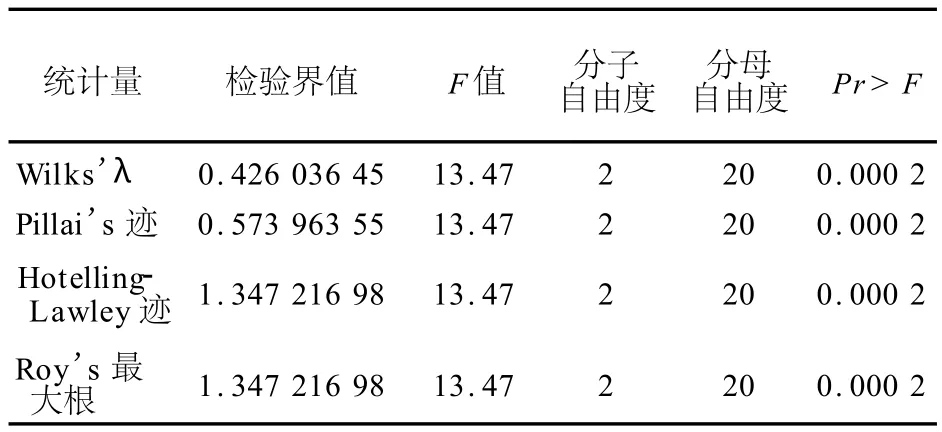
对于没有第二组与第三组组间效应的假设所做的多元方差分析的检验界值和近似 F值H=第二组与第三组组间比较离差矩阵E=误差离差矩阵MANOVA test criteria and exact F statistics for the hypothesis of no overall group 2 vs group 3 effect H=con trast SSCPmatrix for group 2 vs group 3 E=error SSCPmatrix S=1 M=0 N=9

统计学和专业结论:三组观测结果的差异具有统计学意义,根据上面分析可知,高剂量褪黑素组可以明显降低大鼠体重和腹腔脂肪组织量。

[1] 杨凌辉,刘志民,李文桐,等.褪黑素对大鼠腹腔内脂肪组织代谢的影响[J].药学服务与研究,2005,5(1):23-24.

Yang LingHui,Liu ZhiMin,Li Wen Tong,et al.Effect of melatonin on metabolism of intra-abdominal fat of rat[J].Pharm Care Res,2005,5(1):23-24.

[2] 胡良平.医学统计学:运用三型理论分析定量与定性资料[M].北京:人民军医出版社,2009:49.

Hu LiangPing.Medical statistics:analysis of quantitative and qualitative data with triple-type theory[M].Beijing:People’s M ilitary M edical Press,2009:49.Chinese.