包含多重Zeta函数的若干个恒等式

沈忠燕

(浙江外国语学院理工学院,浙江杭州310012)

1 引 言

多重Zeta函数

又称Euler-Zagier和,近年来引起不同方向许多学者的广泛关注.各种多重Zeta函数不仅对一般的Zeta函数理论研究是很重要的,而且对代数几何、上同调理论、扭结理论和量子力学等的研究是非常有意义的.

1997年,Borwein,Bradley和Broadhurst[1]考虑了带符号的多重Zeta函数

其中,σj∈{-1,1},j=1,2,…,k.为了书写的方便,如果σj=1,相应的变量记为sj,如果σj=-1,相应的变量记为-sj.

与多重Zeta函数有关的许多恒等式是非常漂亮而且又有意义的.对某一数列的n次重复,在文献[1]中,Borwein,Bradley和Broadhurst证明了的,如

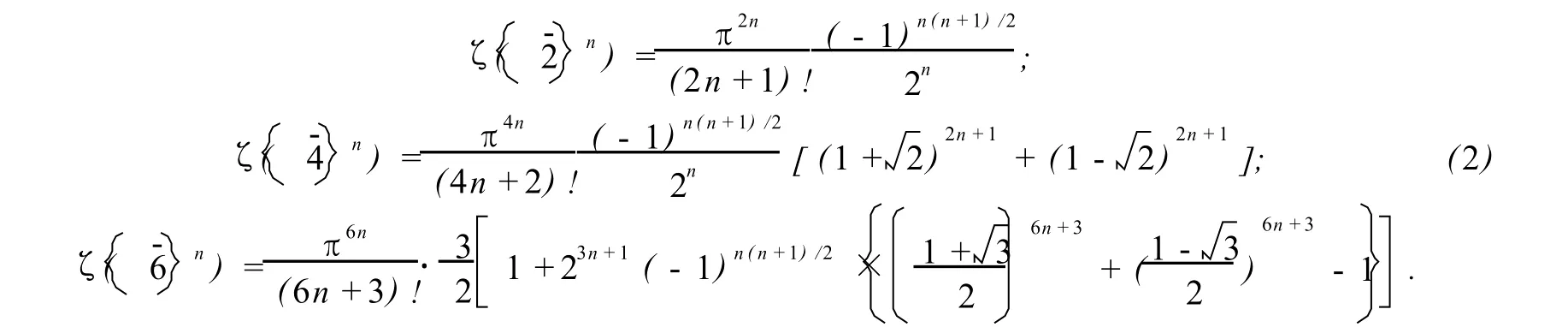
Granville等[2]在2004年证明了若N和r均为正整数,N≥r,则

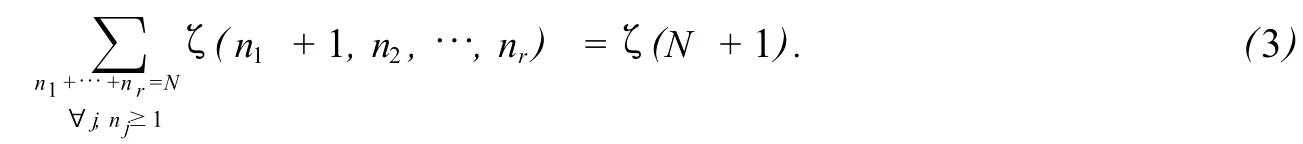
此公式r=3的情形由Hoffman和Moen证明,r=2的情形由Euler证明,即当n≥3时,

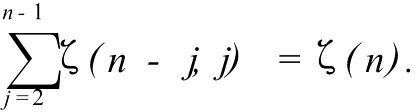
2 定 理

在本文中我们得到了以下定理.

2.1 定理1 当正整数r,s满足rs≥2时,有

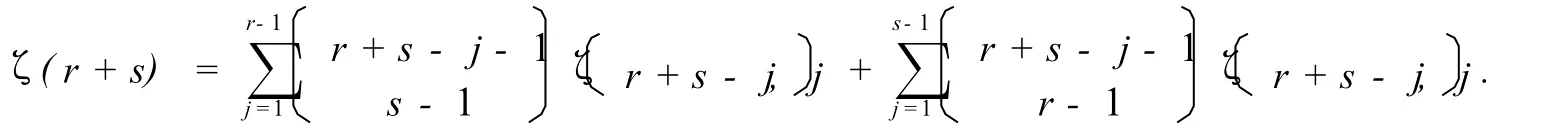
对任意的正整数r,s,有

当正整数r,s满足r≥2,s≥1时,有

推论1 当n≥2时,有

2.2 定理2

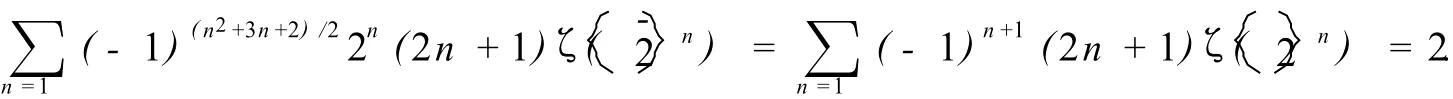
H.Gangle,M.Kaneko和D.Zagier[3]证明了当n≥2时,

2009年,T.Nakamura[4]给出了(4)的一个新的证明.最近,蔡天新和作者证明了当n≥3时,

当n≥4时,

当n≥5时,

利用(4)-(7),我们得到了以下定理.

2.3 定理3 对任意的实数m＞1,有

若在定理3中取m=2,下列等式成立:

最近蔡天新和作者证明了当n≥2时,

当n≥3时,

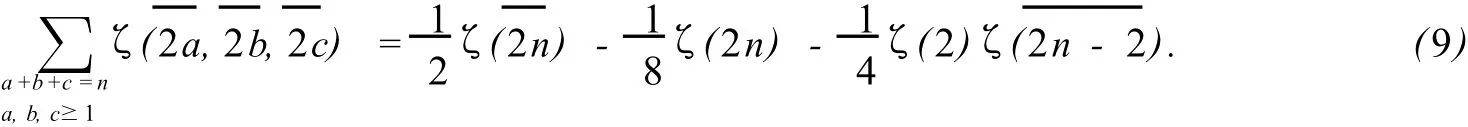
当n≥4时,

利用(8)-(10),我们得到了以下定理.

2.4 定理4 对任意的实数m＞1,有

若在定理4中取m=2,有下列等式成立:

多重Hu rwitz Zeta函数

也受到广泛的关注.蔡天新和作者证明了当n≥2时,

当n≥3时,

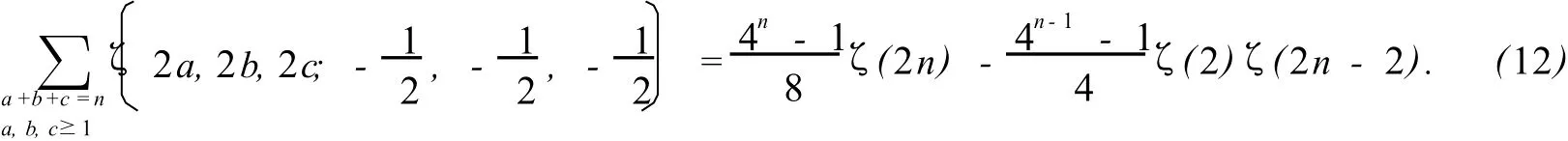
当n≥4时,

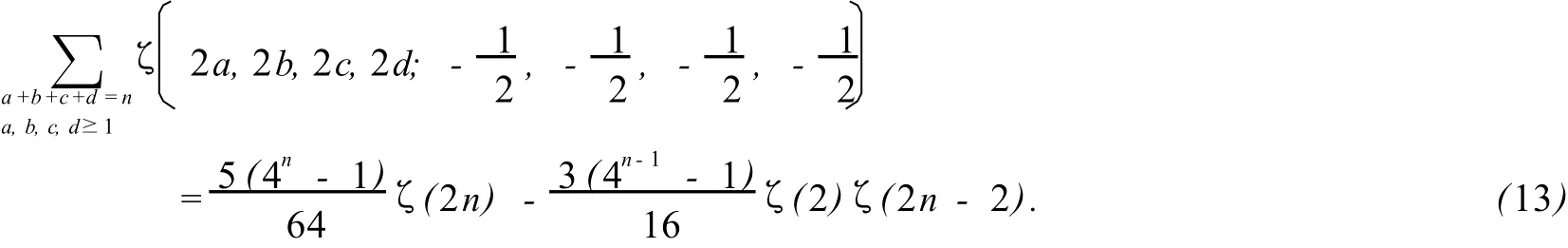
当n≥5时,

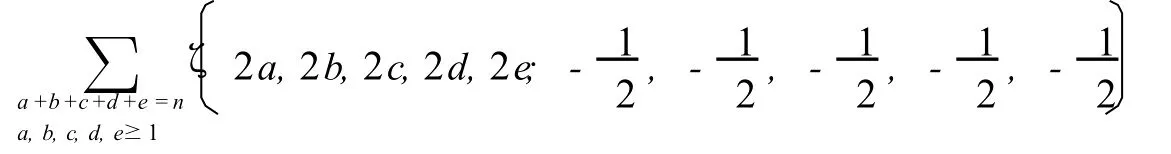
利用(11)-(14),我们得到了以下定理.

2.5 定理5 对任意的实数m＞2,有

若在定理5中取m=4,有下列等式成立:

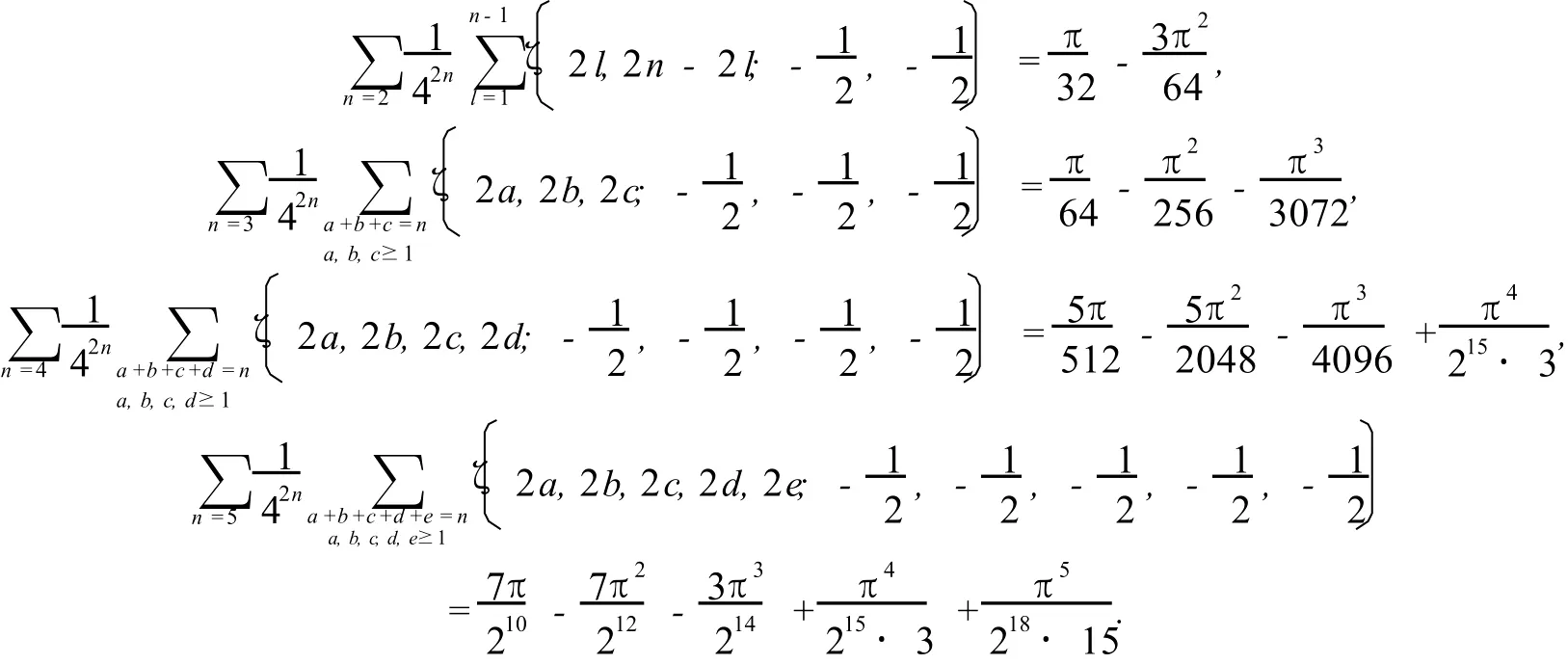
3 引 理

为了证明定理,我们需要下面两个引理.

3.1 引理1[5] 若r-1和s-1为正整数,则

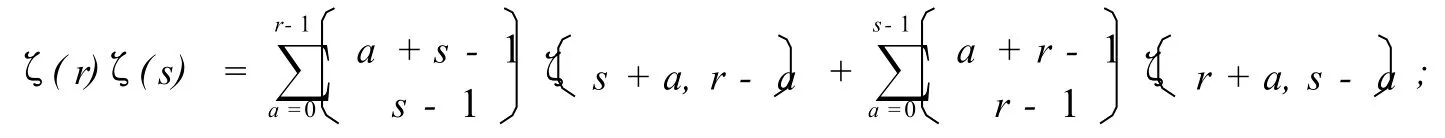
若r和s为正整数,则

若r-1和s为正整数,则

3.2 引理2 对任意的实数m＞1,

证明 因为

这里B是第k个Bernoulli数,满足

k

因此引理2得证.

4 定理的证明

4.1 定理1的证明

由调和乘积公式,当正整数r,s满足r≥2,s≥2时,我们得到

联合引理1我们得到

第一个和式作变量代换r-a→j,第二个和式作变量代换s-a→j,我们有

当r,s中有一个为1时,由(3)式知,上式也成立.

由调和乘积公式,对任意的正整数r,s,我们有

联合引理1以及作相同的变量代换我们得到

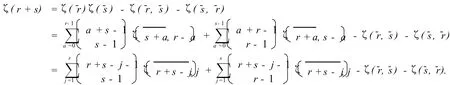
由调和乘积公式,当正整数r,s满足r≥2,s≥1时,我们得到

联合引理1以及作相同的变量代换我们有

因此定理1得证.

在定理1中令r=s=n,我们得到推论1.

4.2 定理2的证明

我们知道ex的幂级数展开式为

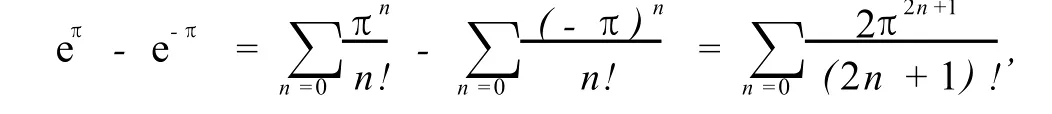
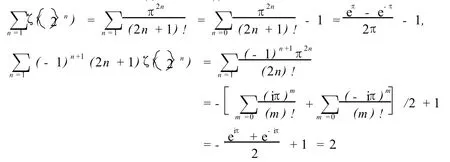
因此定理2得证.

4.3 定理3的证明

因此定理3得证.

4.4 定理4的证明

因此定理4得证.

4.5 定理5的证明

因此定理5得证.

[1]Bor wein J M,BradleyD M,Broadhurst D J.Evaluations of k-fold Euler/Zagier sums:A compendium of results for arbitraryk[J/OL].[2010-12-10].The Electronic Journal of Combinatorics,1997,2(4).http://www.combinatorics.org/Volume_4/PDF/v4i2r05.pdf.

[2]Granville A.A decomposition of Riemann’s zeta function[J].Analytic Number Theory,1996,247:95-101.

[3]Gangl H,KanekoM,ZagierD.Double zeta values and modular for ms[C]//Böcherer S.Proceedings of the conference in memory of Tsuneo Arakawa:Automorphic Forms and Zeta Functions.Singapore:World Scientific,2006:71-106.

[4]Nakamura T.Restricted and weighted sum formulas for double zeta values of even weight[J].Šiauliai Math Semin,2009,4(12):151-155.

[5]Zhou X,Cai T,Bradley DM.Signed q-analogs of Tornheim’s double series[J].Proc Amer Math Soc,2008,136:2689-2698.