往复式压缩机振动的有限元数值分析与实验研究
2011-01-25仲崇明蒋伟康
仲崇明,万 泉,蒋伟康
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
往复式压缩机振动的有限元数值分析与实验研究
仲崇明,万 泉,蒋伟康
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
对某型往复式冰箱压缩机的振动进行了有限元数值模拟,研究了曲轴-连杆-活塞运动系统产生的机械激励引起的压缩机振动响应。研究表明,曲轴-连杆-活塞运动系统是压缩机低频振动的主要激励来源,气体力主要引起压缩机泵体的水平扭转振动。通过仿真结果和试验的对比,验证了数值模拟方法应用于压缩机振动响应分析的可行性。通过数值模拟,可得到机械激励引起的壳体表面振速分布,为压缩机的机械噪声预测提供参考。
往复式压缩机;有限元法;振动响应
压缩机作为电冰箱主要的振动和噪声源,越来越受到冰箱生产厂家的重视。现阶段冰箱压缩机中普遍采用的是往复式压缩机。冰箱压缩机噪声源包含:机械噪声(不平衡力和不平衡力矩,摩擦激发以及阀片的运动冲击等),气动噪声,电机噪声等[1]。其中,曲轴-连杆-活塞运动系统的往复运动产生的不平衡力及力矩和旋转运动产生的离心力是产生压缩机振动和机械噪声的重要原因之一[2]。
之前有关往复式压缩机壳体振动辐射噪声问题的研究,主要集中于不同壳体参数、泵体连接方式及润滑油的存在对壳体固有频率的影响[3-6];或采用压缩机动力学理论计算优化曲轴-连杆-活塞系统结构参数,以降低机械激励[7]。有限元等数值模拟方法在压缩机振动响应预测中的应用尚不多见,仅黄兹思[8]采用有限元方法分析了双转子压缩机壳体在机械激励下的振动响应,而有关往复式压缩机的壳体振动响应的数值模拟未见诸报道。
本文采用有限元法分析了某型往复式压缩机在机械激励下的壳体振动响应,并进行了试验验证,为预测压缩机的机械噪声提供参考依据。
1 往复式压缩机动力学计算
往复式压缩机的运动机构在外界动力的驱动下,受到各种力的作用。由于这些力之间的相互作用,产生了平衡、振动等一系列问题[9]。
1.1 不平衡力
当压缩机正常工作时,作用于曲柄连杆机构上的力主要有三种:① 惯性力;② 气体压力的作用力——气体力;③ 摩擦力。至于各机件本身的重力,因其作用相对较小,故可忽略不计。
曲柄连杆机构中的惯性力包括三方面:一是活塞往复运动产生的惯性力;二是连杆运动产生的惯性力;三是曲柄不平衡旋转质量的离心惯性力。
研究连杆惯性力,就是要找出它传给活塞和曲柄的力的大小与方向。将连杆实际的分布质量用假想的集中质量来代替,使后者所产生的惯性效果与前者相同。连杆质量mc的一部分mc1集中在大头中心,另一部分mc2集中在小头中心。得到下面的方程式:

式中,L为连杆大头质心到小头质心的距离,l1为连杆质心至小头中心的距离。mc1可以视作与活塞一起的往复质量,mc2可以视作与曲柄销一起的旋转质量。
曲柄连杆机构的往复惯性力Fj是活塞组质量和集中质量mc1相加之和mj产生的往复惯性力。

式中,ω为圆频率,λ=r/L,r是曲轴中心线与曲轴销中心线之间的距离,α是曲轴转角。
旋转惯性力Fr是换算到连杆大头中心处的曲轴不平衡旋转质量ms和集中质量mc2所产生的离心惯性力之和。
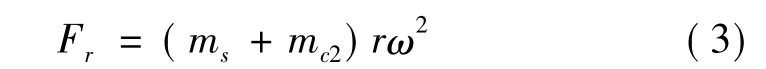
作用于活塞的气体力Fg为活塞两侧气体压力差与活塞面积的乘积:

式中p是气缸内瞬时压力,pca是吸气压力,Ap是活塞横截面积。
作用在活塞上的往复摩擦力Fmp其大小随曲柄转角而变化,但为简化计算,一般假设为常值,而方向则始终与活塞的速度方向相反。
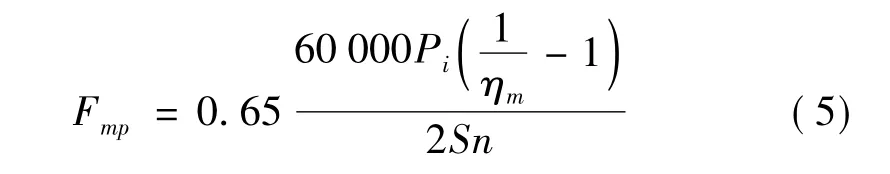
式中Pi是压缩机的指示功率,单位为kW;ηm是机械效率;S是活塞行程,单位为m;n是转速,单位为r/min。
1.2 倾覆力矩
如果忽略压缩机本身各零件重力,主要作用力是气体力、惯性力和摩擦阻力,分析它们对压缩机动力平衡的影响。
活塞力Fp(即气体力、往复惯性力、往复摩擦力)在活塞销处分解出作用于缸壁上的侧向力,而连杆力传到主轴承座处也可分出一侧向力,二者大小相等,但方向相反,形成一力偶,这个力矩使压缩机在水平面内摆振,被称为倾覆力矩MD。

要减少压缩机由倾覆力矩所引起的摆振,一般只能依靠足够大的安装基础或弹性支承方法来达到。旋转惯性力Fr使压缩机有前后左右跳动的趋势,但其几乎可由平衡质量完全抵消掉,故忽略。
1.3 频域激励力和激励力矩
由式(2)、式(5)、式(6)计算得到时域往复惯性力、摩擦力及其引起的倾覆力矩,再进行傅里叶变换,得到频域上的激励力和激励力矩,如图1、图2所示。
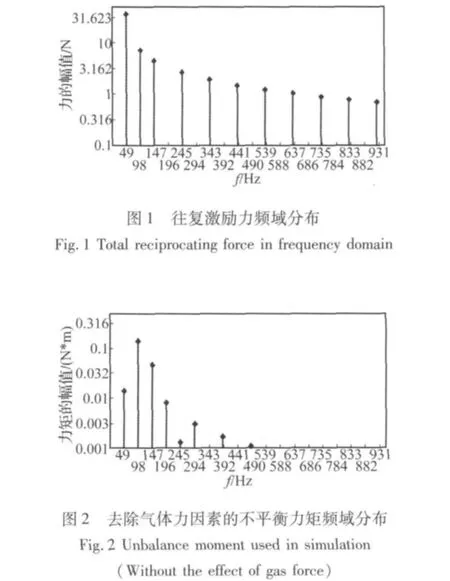
气体力并不直接激励压缩机振动,而是作为活塞力的一部分产生倾覆力矩。根据式(6),计算得到气体力独自引起的倾覆力矩,如图3所示。比较图2、图3可知,气体力在倾覆力矩中占主导。

图3 气体力导致的不平衡力矩频域分布Fig.3 Unbalance moment caused by gas force
2 仿真分析
2.1 有限元模型
压缩机有限元模型包括泵体(由气缸铸件和电机定子组成),弹簧,外壳,机脚等。泵体和外壳之间采用弹簧连接,外壳和机脚采用点焊连接。有限元模型中不包括电机转子,曲柄-连杆-活塞机构,平衡块等运动部件,因为已将它们对系统的作用考虑到激励力之中。
(1)泵体有限元建模:
在保证分析精度前提下,将压缩机泵体Pro/E三维模型(含弹簧)作适当简化以利于网格划分,具体包括:删除零件中的倒角、小孔及小尺寸的圆角等特征,将螺栓连接采用固定连接代替。
若将简化后的实体模型直接导入ANSYS,则由于简化后的模型仍含有内部腔及弹簧细小截面等复杂结构,导入后出现面、体丢失和布尔操作失败。因此,首先采用Pro/E Mechanical模块有限元分析的前处理功能为泵体和弹簧划分网格,保证相邻部件在接触位置处共节点。然后,将划分好的网格导入ANSYS,建立有限元模型,单元类型为Solid92,如图4所示。
(2)壳体有限元建模
在Pro/E模型中对外壳、机脚的实体模型抽取包络面,导入ANSYS中,然后删除多余部分再划分为壳网格,单元类型为Shell63,并定义实常数,如图5所示。
(3)模型连接部分
在有限元模型中,采用ANSYS中的刚性区域(Rigid region)功能模拟弹簧与外壳、机脚和外壳的连接。刚性区域是通过建立约束方程固结两个不同单元类型的区域,实现力及力矩的传递。参照压缩机实际工作情形,约束机脚圆孔所有自由度,如图5所示。

2.2 分析步骤
将图1-图2中不考虑气体力因素的激励力和力矩加载到压缩机泵体上。利用ANSYS软件,在基频48.67 Hz及其整数倍频率上作压缩机泵体、外壳的结构谐振响应分析,得到泵体及外壳的节点位移分布,然后得到泵体节点振速及外壳法向振速分布。
2.3 仿真结果
以前48.67 Hz的谐振响应分析为例,说明压缩机振动特性。定义泵体上气缸轴向为水平长轴方向、与气缸轴垂直方向为水平短轴方向。
48.67Hz激励源特点为:往复激励力(往复惯性力与摩擦力组成)占主导,而不平衡力矩相对小很多。泵体合位移如图6所示,气缸上端合位移幅值最大,合位移在泵体的分布至上而下逐渐减小。
外壳合位移最大处位于壳体顶端,如图7所示。
如图8所示,泵体三个分向位移在水平长轴方向最大,竖直方向次之,水平短轴方向最小,约比其它两个方向上小10倍左右。
泵体分向位移经弹簧传递到外壳,由有限元仿真结果来看,特别是在竖直方向和水平长轴方向上,泵体与外壳分向位移分布趋势一致,传递特征明显。泵体振动传递到壳体振动,分向位移幅值分别下降为原来的1/100、1/40和1/100左右。

图8 48.67 Hz泵体到外壳的三向振动传递Fig.8 Vibration transmission of 48.67 Hz
将有限元节点位移作为边界条件加载到边界元仿真软件的外壳单元模型后,可得到48.67Hz外壳节点的法向振速。如图9,观察法向振速在外壳的分布,发现幅值较高区域集中在压缩机启动器上端及其相对另一侧上端,在外壳顶端、铭牌面及对面中心带、外壳底部和弹簧底座部位振速幅值较小。法向振速在外壳表面过渡均匀、高低变化趋势明显。
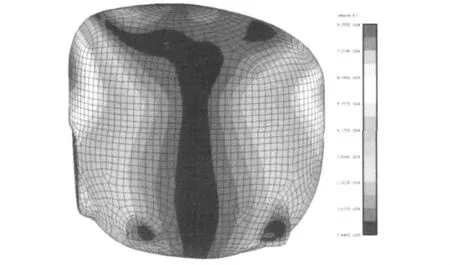
图9 48.67 Hz外壳振速幅值分布Fig.9 Velocity amplitude distribution on shell
类似地,可预测得到其它频率下压缩机振动情况。例如,97.33Hz的仿真结果表明泵体分向位移在水平长轴、短轴和垂直方向上的幅值相差不大,这应该是由于激励力与激励力矩大小相当,导致水平扭转明显。
3 振动测量试验
压缩机试验模型1:将压缩机气缸端盖、阀片、消声器,排气管拆除,去除外壳上盖。
压缩机试验模型2:将压缩机气盖端盖、阀片、消声器,排气管拆除,保持外壳封闭。
3.1 泵体振动测量
通过试验模型1的四只圆孔,用螺栓将机脚压紧在刚性试验台上,如图10所示。
这里,由于拆除了气缸端盖、阀片,消除了气体力影响,只保留机械不平衡力激励。将压缩机接至50 Hz频率交流电运转,使用单向加速度计分别测量泵体(Corner1-4)附近的水平长轴(即气缸轴)、水平短轴(与气缸轴向垂直)和垂直方向的加速度。
3.2 壳体振动测量
在试验前首先将试验模型2内腔用真空泵抽真空,直至腔内压强低至10 Pa-20 Pa,模拟近似真空状态。将压缩机接至50 Hz频率交流电运转。在压缩机外壳上布置3个加速度测点,分别位于:启动器对面,铭牌对面,及壳体顶端。
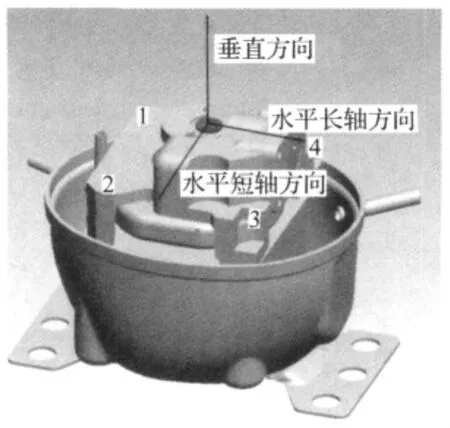
图10 泵体上各测试方向及测试点定义Fig.10 Definition of directions and points
4 振动仿真与测量数据对比
4.1 泵体振动仿真与测量数据对比
将测点上三个方向振速幅值的仿真结果与试验值对比,如表1所示。
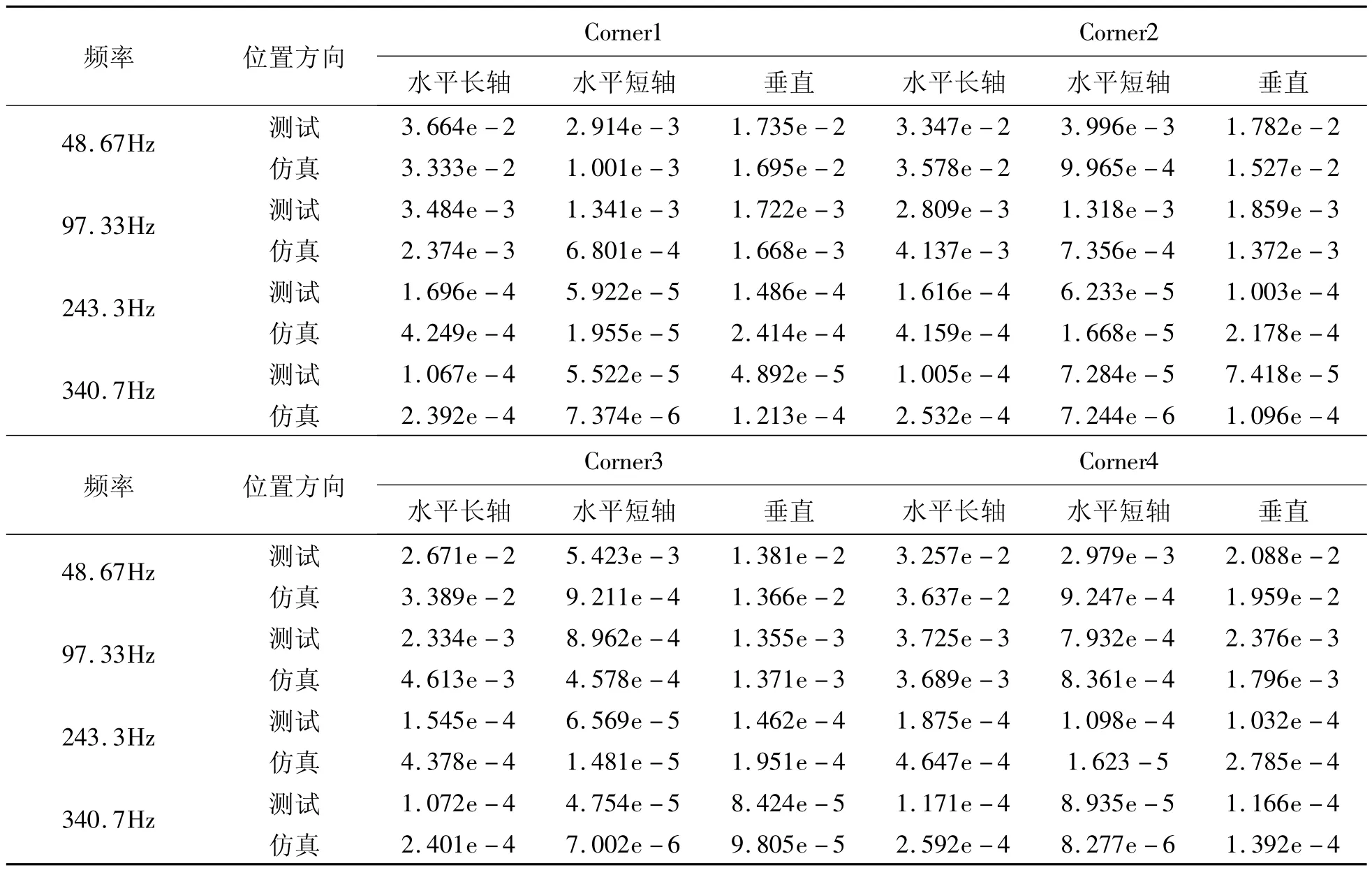
表1 泵体振速的测试与仿真数值比较(单位:m/s)Tab.1 The comparison about the vibration of pump body between simulation and measurement(Unit:m/s)
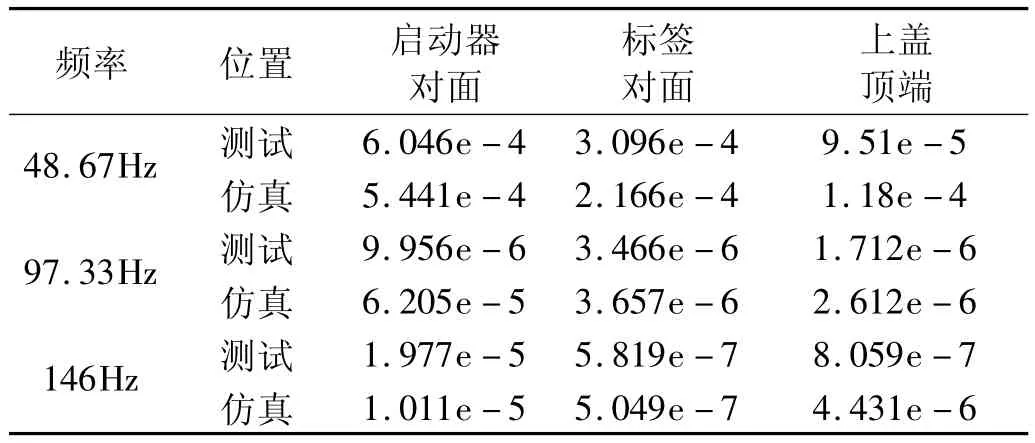
表2 壳体振速的测试与仿真数值比较(单位:m/s)Tab.2 The comparison about the shell vibration between simulation and measurement(Unit:m/s)
对比结果表明,在 48.67 Hz、97.33 Hz 上,仿真结果与试验值吻合较好;在 243.3 Hz 、340.7 Hz上,水平长轴和垂直两个方向上仿真结果与试验值吻合较好;但是,在水平短轴方向,仿真结果远小于试验值,后者甚至相差一个数量级。原因可能是:① 在测试时为去除润滑油与壳体振动的耦合作用,没有添加润滑油,导致旋转摩擦力增大,会加剧水平短轴方向的振动;② 曲轴-连杆-活塞系统加工和安装误差也会增加不平衡力矩,加剧水平方向扭转振动。
4.2 壳体振动仿真与测量数据对比
结果如表2所示,在频率48.67 Hz等较低频率上,仿真结果与测试值吻合较好。但是随着频率增加差异逐渐增加,可能由于以下因素引起:① 压缩机内存留相当容积的油液,影响了壳体振动;② 仿真中没有考虑泵体的电机振动;③ 加工和安装精度误差会加剧壳体振动。
5 仿真分析气体力对泵体振动的影响
考虑气体力因素对机械激励的影响后重新做谐响应分析,在340.7Hz上泵体振动仿真结果的对比如表3所示。从两次不同激励下仿真结果的比较,可以看到:不平衡力矩考虑气体力因素后,泵体振动仿真结果在水平短轴方向有明显增加,说明气体力主要引起压缩机泵体的水平扭转振动。

表3 气体力对泵体振动的影响(单位:m/s)Tab.3 The effect of gas force to pump body vibration(Unit:m/s)
6 结论
采用有限元仿真分析了曲轴-连杆-活塞运动系统产生的不平衡力和力矩引起的压缩机振动响应,通过与试验对比,表明数值模拟能够应用于压缩机振动响应分析,得到机械激励引起的壳体表面振速分布,为压缩机的机械噪声预测提供参考。研究结果表明,曲轴-连杆-活塞运动系统是压缩机低频振动的主要激励来源。气体力对压缩机泵体振动,特别是水平面内的扭转振动影响显著。
在此基础上可对压缩机进行改进,改进措施包括:对曲轴-连杆-活塞机构的动平衡、壳体、气阀、支撑弹簧等进行优化设计;降低泵体重心、改变内排气管的成型布置、调整润滑油量等。
[1] Suzuki S.Noise control of domestic facilities[J].Int.J.Japan.Soc.Prec.Eng,1998,32(3):166 -170.
[2]杨伟成.家用小型制冷压缩机的噪声控制[J].家用电器科技,1999(4):16-19.
[3] Kuznetzov L.Piston compressor vibration and noise reduction[M]. Westminister:ProfessionalEngineering Publishing Ltd,2003.
[4]舒歌群,韩 睿.往复式压缩机噪声诊断及降噪研究[J].压缩机技术,2004(1):8-11.
[5]骆江锋.降低往复式压缩机振动与噪声的设计[J].食品与机械,2006,22(6):91 -94.
[6]陈建良,金 涛,孟晓宏,等.冰箱压缩机壳体噪声辐射数值分析[J].浙江大学学报(工学版),2007,41(5):794-798.
[7]张继德.冰箱压缩机运动系统动平衡探讨[J].机械设计,1999(11):41-44.
[8]黄兹思,蒋伟康,周 易.双转子压缩机振动的有限元数值分析与实验研究[J].机械强度,2004,26(6):620- 623.
[9]缪道平.活塞式制冷压缩机[M].北京:机械工业出版社,1992.
Numerical analysis and tests for vibration response of a reciprocating compressor
ZHONG Chong-ming,WAN Quan,JIANG Wei-kang
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University,Shanghai 200240,China)
The FEM method was used to study vibration response of a reciprocating compressor excited by mechanical excitations of a crank-connectingrod-piston system.It was shown that the crank-connectingrod-piston system is the main excitation source for low-frequency vibration of the reciprocating compressor,and the gas force is the main cause of the horizontally torsional vibration of its pump body.Some tests were implemented to validate the feasibility of the FEM method in the dynamic response analysis of the reciprocating compressor.The normal velocity distributions on the compressor shell due to the mechanical excitations were obtained with FEM method,on their basis the prediction of the mechanical noise became possible for the reciprocating compressor.
reciprocating compressor;finite element method(FEM);vibration response
TB532;TB652
A
2009-12-16 修改稿收到日期:2010-01-26
仲崇明 男,硕士生,1984年生
万 泉 男,讲师,1978年生
