弹簧振子势能问题的探讨

冯蒙丽 宋春荣 刘协权

(石家庄军械工程学院基础部 河北 石家庄 050003)

在大学物理中，以能量守恒和转换的观点去研究具体运动形式所遵循的规律是物理学基本的研究方法[1]．而对于重要的运动基本形式之一——简谐振动,有的教材未对其能量作充分的讨论[2]．

在讲解弹簧振子能量时，由于某些教材及教师对系统内成对保守内力做功、参照系选取等内容强调不够,使学生不能准确理解弹性势能的概念[3]．水平放置和竖直放置的弹簧振子其振动表达式相同，动能和势能表达形式也一样，物理意义却完全不同；前者为单纯振子与弹簧组成系统的弹簧性势能,而后者却是振子在弹性力势场和重力势场组成的复合势场中运动时，复合势场所对应的势能，即为弹性势能与重力势能的叠加．这部分的讲解涉及到对势能定义的理解，也是学生理解的难点.在与水平弹簧振子进行对比的基础上，从两个角度对竖直弹簧振子的能量进行分析．

1 水平放置的弹簧振子能量

水平放置的弹簧振子如图1所示.简谐振动的动力学方程为

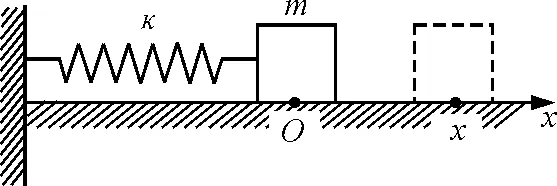
图1

其运动学方程为

x=Acos(ωt+φ)

水平放置的弹簧振子的动能为

势能(弹性势能)为

总机械能

E=Ek+Ep=

2 竖直放置的弹簧振子能量势能零点的选择

竖直放置的弹簧振子能量，教材中通常只给出动力学方程，然后给出弹簧振子势能仍为

2.1 以弹簧平衡点为势能零点

通常研究讨论中会以平衡点作为弹簧势能和重力势能零点． 如图2所示, 竖直放置弹簧振子，设轻弹簧的劲度系数为κ，原长为l0，振子质量为m，平衡状态下弹簧伸长到l．以平衡点为坐标原点，建立如图2所示坐标系．

当振子偏离平衡点x时，则弹簧振子势能为

上式右边方括号内为弹性势能，后边圆括号内为重力势能.

图2 弹簧平衡点为势能零点

又因为

mg=κ(l-l0)=κΔl

所以

可见重力势能恰好与部分弹性势能互相转换而抵消.由mg=κΔl可知，重力被抵消，使系统的总势能不出现重力势能．

这是通常采用的方法.对于两个势能采用一个势能零点，优点在于推导简便，有助于深刻理解势能相对性的内涵；缺点在于按照初学者的惯性思维，对于重力势能的相对性应用熟练，而弹性势能仍旧习惯采用原长为弹性势能零点.笔者认为依照惯性思维循序渐进进行学习讲解，也不失为一个好办法．

2.2 以弹簧原长为势能零点

弹簧振子系统不变，以弹簧原长为弹性势能零点(图3).对于重力势能零点选取待定，为了探讨的方便，我们暂时使重力势能为mgh．则

上式右边方括号内为弹性势能，后边圆括号内为重力势能，即

又因为

mg=κ(l-l0)=κΔl

所以

得

可见只要选取一个重力势能零点，使得此式成立，即可满足系统势能为

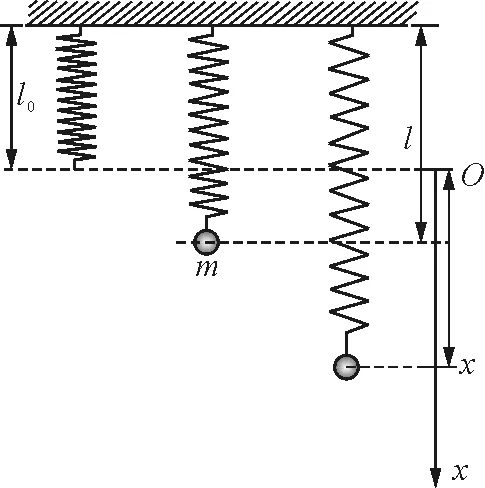
图3 以弹簧原长为势能零点

这种方法优点在于按照学生的认识规律学习，易于理解接受；缺点在于选取两个势能零点稍显繁琐．

3 结束语

实践证明第二种方法对初学者讲解效果更佳.可在第二种方法的基础上再介绍第一种方法，既有利于学生对弹簧振子能量的理解，又能更加深刻理解势能零点选取的相对性．

参考文献

1 杨青勇,李作春.简谐振动系统的势能，南宁师范高等专科学校学报, 2001( 4 )：75～77

2 康颖.大学物理.北京：科学出版社，2005.139～140

4 熊正文.关于弹性势能与势能零点和坐标原点选取问题的讨论.黔东南民族师范高等专科学校学报，2002(12):11～12