双喷嘴挡板电液伺服阀主要参数的优化

黄 浩，周 渊，陈奎生，雷辉虎

（武汉科技大学机械自动化学院，湖北武汉，430081）

电液伺服阀是液压伺服系统中的核心控制器件，起着连接液压和电气的纽带作用，其代表性产品有喷嘴挡板式、射流管式、射流式和动圈滑阀式等类型。双喷嘴挡板电液伺服阀由于具有控制精度高、响应速度快、死区小、运动平稳和结构紧凑等特点，在冶金和军工领域均得到广泛的应用。目前国内外对双喷嘴挡板电液伺服阀的研究主要集中在优化结构参数、采用新材料和新内部结构等方面，而电液伺服阀的动态性能是由液压系统的工况和伺服阀的结构参数决定的，优化伺服阀的结构参数对改善伺服阀的动态性能、提高伺服阀的响应速度具有重要的意义［1］。为此，本文以国产双喷嘴挡板电液伺服阀为研究对象，推导出相关数学模型，并通过分析伺服阀动态性能的变化，从而达到其参数优化的目的。

1 数学模型描述

双喷嘴挡板电液伺服阀由力矩马达和液压放大器组成，第一级为双喷嘴挡板，第二级为四通滑阀，其动态方程可由以下4个基本方程来确定。

1.1 力矩马达运动方程

力矩马达传递函数为

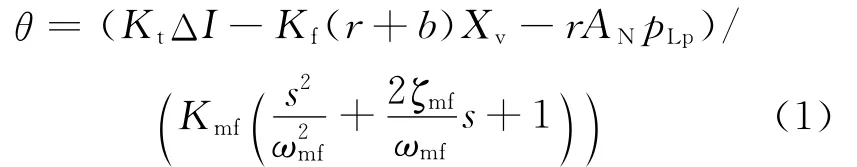
式中：θ为衔铁转角，rad；Kmf为力矩马达的总刚度［2］（综合刚度），N／m；ωmf为力矩马达的固有频率，其中，Ja为衔铁组件的转动惯量，kg·m2；ξmf为力矩马达的阻尼比，ζmf其中，Ba为衔铁的粘性阻尼系数；Kt为力矩马达的电流－力矩增益；ΔI为输入电流，A；Kf为反馈杆刚度，N／m；r为喷嘴中心至弹簧管回转中心的距离，m；b为反馈杆中心至喷嘴中心的距离，m；Xv为阀芯位移，m；AN为喷嘴孔的面积，m2；pLp为两喷嘴孔压力差，Pa。

1.2 挡板位移与衔铁转角的关系

挡板位移Xf与衔铁转角θ的关系为

式中：Xf为挡板的位移，m。

1.3 喷嘴挡板阀控制阀芯的传递函数

喷嘴挡板阀控制阀芯的传递函数为

式中：Kqp为喷嘴挡板阀的流量增益；Av为主阀芯端面面积，m2；ωhp为滑阀的液压固有频率，rad／s；ξhp为滑阀的液压阻尼比。

1.4 伺服阀传递函数

伺服阀简化后总的传递函数为式中：Kvf为力反馈回路开环放大系数，Kvf＝r（r＋b）KtKqp／（AvKmf）；Kxv为伺服阀增益［3］，Kxv＝Kt／（r＋b）Kf；Ka为伺服放大器增益，Ka＝2Ku／（Rc＋rp），其中，Ku为放大器每边的增益；Rc为每个线圈的电阻，Ω；rp为线圈回路的放大器内阻，Ω。

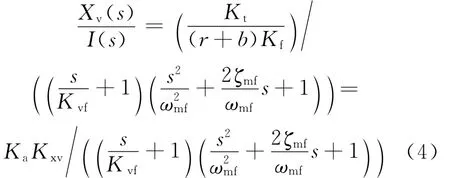
2 目标参数

影响伺服阀综合性能的主要参数有：Kt、和Kf，其中Kt是力矩马达增益，它处于闭环系统之外。当力矩马达装入伺服阀后，Kt可由放大器数字调节，单独研究的价值不大。Kqp为喷嘴挡板阀流量增益，它取决于第一级泄漏流量和喷嘴与挡板之间的零位间隙大小，且Kqp受泄漏流量和力矩马达功率的限制，对固定型号的喷嘴挡板阀变化不大。属于力矩马达机械阻尼比。所以对伺服阀动态性能的影响主要研究四个参数［4］。考虑到4个参数之间的耦合关系，在此引入另一个力反馈回路开环放大系数Kvf，即：

当喷嘴挡板上液动力忽略不计、衔铁挡板的净刚度Kan＝0时，即：

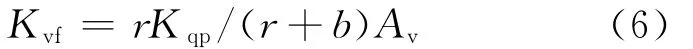
由式（6）可知，Kvf和Av呈反比，与r／（r＋b）的比值和流量增益Kqp呈正比［5］，即：

由式（7）可得，ωmf与力矩马达的综合刚度Kmf根号呈正比，与衔铁组件的转动惯量Ja根号呈反比。从频率法上看，对于任何伺服阀，当0.707时，系统具有较好的稳定性和较好的动态性能，但实际上伺服阀的阻尼比难达到此理想值，因此对伺服阀参数的优化主要集中对3个参数进行优化［5］。

3 参数优化

伺服阀参数优化的通常方法是利用Parseval定理，再将函数优化转化为变量优化。选择电液伺服阀的结构参数作为设计变量，以系统稳定性、快速性、稳态误差最小为目标函数，建立伺服阀机构优化模型，从而达到伺服阀参数优化的目的［6］。

通过分别对4个目标参数求偏导数，然后再进行全微分，就可以得到主要参数与系统的关系。我们求得一组在稳定性条件下的伺服阀参数，运用Matlab软件中的Simulink模块仿真，对伺服阀的闭环传递回路进行仿真。通过改变目标函数的大小，得出伺服阀闭环伯德图。对比仿真图形，分析改变目标参数后的系统频宽变化，从而得到目标函数与伺服阀动态性能的关系，完成了目标参数的优化。

3.1 力反馈回路开环增益Kvf的优化对比

当Kvf＝900、Kvf＝1 400时，其他参数不变，依据Simulink仿真得出力反馈系统闭环伯德图如图1所示。由图1可看出，增大开环增益使伺服阀的频宽明显增加，但增量有限。

图1 Kvf不同时力反馈回路闭环伯德图对比Fig.1 Force feedback loop closed－loop Bode graph at different Kvf

3.2 力矩马达固有频率ωmf和综合阻尼比的优化对比

图2 ωmf和不同时力反馈回路闭环伯德图对比Fig.2 Force feedback loop closed－loop Bode graph at differentωmf and

4 结论

（1）伺服阀动态性能与很多参数相关，必须在仿真前确立系统的目标函数，只有将耦合度降至最低，才能求出目标函数对系统的影响。

（2）为增大Kvf，可适当增大Kqp和减小Av，以增大伺服阀的频宽来提高响应速度，但增幅有限，因为Kvf受到稳定性的制约，当无限增大时，伺服阀稳定性就会降低。

（3）为增大ωmf和主要可增大力矩马达的综合刚度Kmf和减小衔铁组件转动惯量；也可增大以达到增大系统频宽的目的。

［1］ 方群，黄增.电液伺服阀的发展历史、研究现状和发展趋势［J］.机床与液压，2007，35（11）：162－165.

［2］ 卢长耿，李金良.液压控制系统的分析与设计［M］.北京：煤炭工业出版社，1991：180－200.

［3］ 王春行.液压控制系统［M］.北京：机械工业出版社，2000：90－97.

［4］ Stefanov Y P，Makarov P V，Urkov P V，et al.Dynamic simulation of chip generation and formation in metal cutting［J］.Theoretical and Applied Fracture Mechanics，1997，28：117－124.

［5］ 王幼民.电液伺服阀结构参数优化［J］.安徽机电学院学报：自然科学版，2002，17（2）：13－16.

［6］ 凌俊杰，周自振.提高电液伺服阀频宽的途径［J］.机床与液压，2004，32（18）：113－118.