赋广义Orlicz范数的Orlicz空间中点到EM距离的刻画

段丽芬,杨德清,许 晶

(通化师范学院 数学系,吉林 通化 134002)

1 引言

广义Orlicz范数是段丽芬和崔云安[1]于2006年最先引入的,它与由Orlicz本人[2]于1932年引进的Orlicz范数和Luxemburg[3]于1955年引进的Luxemburg范数等价.但赋广义Orlicz范数的Orlicz空间与赋Orlicz范数的Orlicz空间及赋Luxemburg范数的Orlicz空间理论上有许多不同之处.本文对赋广义Orlicz范数的Orlicz空间中的闭线性子空间EM进行了准确刻画,并讨论了赋广义Orlicz范数的Orlicz空间中的点到EM之间的距离与θ(u)=inf{λ>0∶ρM(u/λ)<∞}的关系.

2 定义及符号

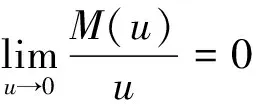
及其闭子空间

EM={x∶∀λ>0,ρM(λx)<∞}

关于Orlicz范数:

Luxemburg范数:

‖x‖M=inf{λ>0∶ρM(x/λ)≤1},

以及广义Orlicz范数:

均成为Banach空间.另外，除特别声明,文中其他符号和定义均同[5].

3 主要结果及证明

证明 对任给ε>0,选正整数n,使得ρM(un)>ρM(u)-ε,其中

因un∈D,故

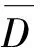
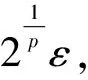
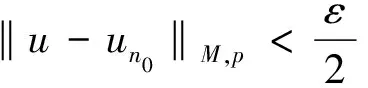
‖χE‖M,p≤‖(u-un0)χE‖M,p+

‖un0χE‖M,p<ε,

⑶⟹⑴记Gn=G(|u(t)|>n),则μGn→0(n→∞).故

‖u-un‖M,p=‖uχGn‖M,p→0(n→∞).

因为un∈EM,EM为闭集,所以u∈EM.

其中θ(u)=inf{λ>0∶ρM(u/λ)<∞}.

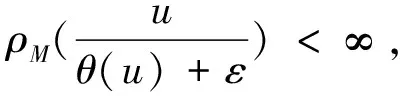
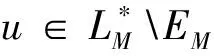
|u(t)-w(t)|>(1-a)|u(t)|

于是

[1]段丽芬,崔云安.广义Orlicz范数和广义Luxemburg范数[J].兰州理工大学学报,2006,32(2):131-134.

[2]ORLICZW.überEineGewisseKlasseVonRäumenVomTypusB[M].Poland:BullAcadPolonaiseA,1932.

[3]LUXEMBURGWAJ.BanachFunctionSpaces[D].Delft-Netherland:TechnischeHogeschoolteDelft,1955.

[4]段丽芬,崔云安.赋广义Orlicz范数的Orlicz空间的端点.[J].浙江大学学报:理学版,2007,34(3):252-256.

[5]CHENST.GeometryofOrliczSpaces[M].Warszawa:DissertationsMath,1996.