基本遗传算法遗传策略优化与Java实现
2011-01-23吴力荣
吴力荣
(浙江工业职业技术学院 人文社科部,浙江 绍兴 312000)
1 引言
遗传算法(Genetic Algorithm,GA)是Darwin生物进化理论的哲学思想启发的搜索技术.GA的基本概念和理论框架,是由Holland首先提出的[1],并由Goldberg作了广泛的探索[2].GA最具有吸引力的特点是它不需要指导搜索的附加知识.一般而言,GA通过生物进化启发的复制、交叉和变异算子搜索字符串的各种结构.模式定理证明了GA具有全局搜索的能力.但经研究表明,若算法结构、操作和参数设计不合理,则遗传算法容易产生早熟收敛.因此,GA研究的重点在于如何避免早熟收敛及均衡GA的全局搜索和局部趋化能力[3-4].迄今已提出许多改进策略,譬如参数自适应、混合或并行GA算法[5].GA早熟收敛的原因本质上可归结为遗失种群多样性.因此,本文一方面引入最优策略,使杂交后适应度高的个体能进入下一代,同时增加筛选策略以维持种群多样性,即基于种群性能差别和种群地域差别删去一些性能相对差的冗余个体,同时随机产生新个体的方法保持种群的多样性.基于典型函数的仿真表明,本遗传算法的全局收敛速度和命中全局最优解的概率均好于传统方法.
2 基本遗传算法
2.1 问题描述
一般需要进行优化计算的实际问题可以表示如下:
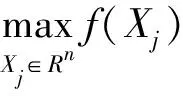
2.2 基本遗传算法过程
Step1:确定决策变量和约束条件,建立优化模型(如2.1).决策变量Xj=(x1,x2,…,xn)(即染色体,也称为个体),组成问题的解空间(即染色体搜索空间).
Setp2:确定编码方法.由于基本遗传算法采用二进制编码,染色体长度根据问题的精度确定,并设计好相应的解码方法.
Setp3:确定个体评价方法.
Setp4:初始化种群.在约束条件下,利用随机生成函数initialize随机生成popsize个个体Xj(j=1,2,…,popsize)作为初始种群P(t),t=0.
Step5:遗传操作.设计遗传算子,对群体P(t)执行遗传操作,产生新种群P(t+1),即下一代群体.遗传操作是遗传算法的精髓所在,主要包括选择、交叉和变异等基本遗传运算.本文将主要对此进行优化.
Setp6:是否满足终止条件.t=t+1,若条件满足输出最优解,结束.否则转向Step5.
3 基本遗传算法遗传策略优化
3.1 交叉保优算法

3.2 筛选策略
在交叉算法中结合保优算法,虽然会提高遗传算法的收敛性和收敛速度,但是降低了种群的多样性,容易使遗传算法收敛到局部最优解.因此需对遗传算法结束后的种群个体进行筛选,将一些冗余个体淘汰,同时随机增加新个体来提高种群的多样性.
为衡量种群的多样性,给出如下定义:
定义1定义种群性能分散度为D(f(X1),…,f(Xn)),即种群P={X1,X2,…,Xn}中各个体性能的方差.
定义2定义种群地域分散度为E(‖X1-G‖,…,‖Xn-G‖).其中,G=E(X1,…,Xn)为种群的重心,‖‖定义欧氏距离.
对种群P筛选步骤如下:
(1)对种群P进行性能筛选.设置阀值为ε,按个体性能的好坏顺序删掉不满足|f(Xi)-f(Xj)|≥ε的个体.剩余个体构成的种群为
P'={X|X∈P,∀i≠j,|f(Xi)-f(Xj)|≥ε}
(2)对P'进行基于地域差别的筛选.记‖Xi-Xj‖=max{|xi,k-xj,k|},设置阀值ω,按个体地域好坏依次删除不满足‖Xi-Xj‖≥ω的个体,得到种群
P"={X|X∈P',∀i≠j,‖Xi-Xj‖≥ω}
(3)若size ofP" 基于二维Rosenbrock函数 Java实现代码见(http://my.oschina.net/thinkinginc/blog/11472). 4.1中的二维Rosenbrock函数,有两个局部极大值,分别是 f(2.048,-2.048)=3897.7342和f(-2.048,-2.048)=3905.9262,其中后者为全局最大值.我们用基本遗传算法和本文优化后的遗传算法分别进行100次运算,得到如下数据: 表1 100次Rosenbrock函数的GA仿真结果 基本遗传算法进化过程与优化后的遗传算法进化过程分别如图1、图2所示: 图1 基本遗传算法进化过程 图2 优化后的遗传算法进化过程 从图中可以看出,优化后的遗传算法,在进化的初始阶段,种群适应度平均值较低,个体具有较好的多样性.在进化的中期,能迅速找到最优值,并收敛于最优值,与基本遗传算法相比较,优化后的遗传算法全局收敛速度和命中全局最优的概率大大提高. 典型的遗传操作在解决问题时存在较大的缺陷,如算法不稳定、易陷入局部极值等.仿真结果表明,本文提出的遗传策略优化后的GA算法,它具有高效率的全局寻优以及良好的稳定性的优点. 参考文献: [1]Holland J H.Adaptation in Natural and Artificial Systems[M].USA:Univ.of Michigan,1975. [2]Goldberg D E.Genetic Algorithms In Search,Optimization,and Machine Learning[M].Addison-Wesley professional,1989. [3]王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001. [4]Gong D,Sun X,Guo X.Novel survival of the fittest genetic algorithm [J].Control and Decision,2002,17(6):908-911. [5]Guo G Q,Yu S Y.Evolutionary parallel local search for function optimization[J].IEEE Trans. on Systems,Man,and Cybernetics,2003,33(6):864-876.4 算法的Java实现与数值仿真
4.1 Java实现代码

4.2 数值仿真



5 结论
