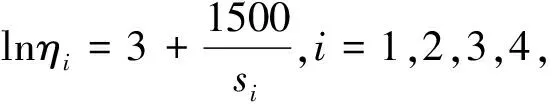Weibull分布恒加试验的Bayes推断
2011-01-23汤银才
武 东,张 青,汤银才
(1.安徽农业大学 理学院,安徽 合肥 230036;2.华东师范大学 金融与统计学院,上海 200241)
1 引言
随着科技的发展和用户对产品质量的要求越来越高,高可靠长寿命的产品越来越多,通常的截尾试验不能满足要求,而加速寿命试验有助于缩短试验时间,常用的加速寿命试验有: 恒定应力加速寿命试验(简称恒加试验)、步进应力加速寿命试验和序进应力加速寿命等.文[1-5]对在CE模型下Weibull分布场合恒加试验进行了统计分析,但上述文献均没考虑到产品在正常应力水平下的先验信息.本文讨论了CE模型下定数截尾情形Weibull分布场合恒加试验的Bayes分析, 对后验分布参数进行了重参数化, 并结合自适应舍选抽样算法和Gibbs抽样法对后验参数进行了Bayes估计.最后,利用蒙特卡罗方法对定数截尾情形Weibull分布场合恒加试验的Bayes估计进行了仿真,通过仿真得到该估计是有效而实用的.
2 基本假定与试验安排
假设1 在正常应力水平S0和加速应力水平S0 (1) 其中ηi,i=0,1,…,k称为应力水平Si下的特征寿命. 假设2 在各种应力水平下,产品的失效机理相同,即m0=m1=…=mk=m. 假设3 产品的特征寿命ηi与加速应力水平Si满足下列加速模型, 即 (2) 其中a,b为参数,φ(Si)是应力水平Si的已知减函数. 在加速应力水平Si下取ni个产品进行定数截尾恒加试验,设在应力Si下的失效时间为 (3) 其中ri为预先给定的中止试验的样本数. 由加速方程知 ηi=η0exp{-b[φ(S0)-φ(Si)]}=η0θ-φi, 于是得到样本的似然函数为 根据工程经验得到加速系数θ的取值范围为1≤k1<θ (4) 产品在S0下, 取ηm的自然共轭分布为逆Gamma分布, 其概率密度为 (5) 其中η>0,a>0,b>0,a和b为超参数. 通常情况下依据历史数据或专家的经验可以确定形状参数m是小于1(对应的失效率单调递减)还是大于1(对应于失效率单调递增).因此若已知m∈(0,1)中,则取b的先验分布为Beta分布, 若已知m∈(1,+∞) 则取m-1的先验分布为Gamma分布.记m的先验分布为π(m)[7].至此,得到m,η,θ的联合后验密度为 (6) 为了计算方便,对参数进行重参数化,作变换 其Jacobi行列式为 则得到λ,μ,m的联合密度为 (7) 下面利用马尔可夫链蒙特卡罗(MCMC)方法的Gibbs抽样来获得参数λ,μ,m的后验分布及Bayes估计. 由(7)知,λ的边际后验分布为 (8) μ的边际后验分布为 (9) m的边际后验分布为 (10) 只要有失效数据, 即r≥1,从而有 容易验证μ和m的边际后验分布均为对数上凸函数,因此μ和m的抽样可按自适应舍选抽样法[7,8]获得. Weibull分布场合恒加试验的Bayes估计可按以下步骤进行: (1)假设起始点为(λ(0),μ(0),m(0)); (2)从边际后验分布π(λ|μ(i-1),m(i-1))抽取λ(i); (3)从边际后验分布π(μ|λ(i),m(i-1))抽取μ(i); (4)从边际后验分布π(m|λ(i),μ(i))抽取m(i); (5)令i=i+1,并返回到(2),直到达到给定终止迭代次数. 则(λ(i),μ(i),m(i),i=1,2,…,M1,M1+1,…,M)为参数(λ,μ,m)的一个Gibbs迭代样本.其中M1为Gibbs迭代抽样达到稳定状态之前舍弃的样本容量,M>M1为总的样本容量.于是λ,μ和m的Bayes估计可用舍弃后的M-M1个Gibbs抽样的样本均值获得, 进而可以得到η,θ,和m的Bayes估计. 以上已经得到Weibull分布步加试验的η,θ和m的Bayes估计,现用Monte Carlo方法进行模拟.步骤如下: (2)从Weibull分布Wei(ηi,m)产生应力水平Si下的定数截尾寿命数据,其中m=0.85,此时Si下的特征寿命η=2422.24,而加速系数θ=1.4924. (4)重复上述模拟100次,然后分别计算不同情形下Bayes估计的相对偏差和相对均方误差. 表1给出了Weibull分布恒加试验的Bayes估计的相对偏差和相对均方误差表.模拟结果表明:在各种情形下,Bayes估计的效果均较好. 表1 Bayes估计的相对偏差和相对均方误差表 参考文献: [1]王炳兴.Weibull分布基于恒加寿命试验数据的统计分析[J].应用概率统计,2002,18(4):413-418. [2]王炳兴.Weibull分布场合具有非常数形状参数恒加试验的参数估计[J].应用数学学报,2004,27(1):44-51. [3]林昌盛.Weibull分布基于恒加试验尺度参数估计[J].纯粹数学与应用数学,2007,23(2): 226-230. [4]仲崇新.威布尔分布场合下恒定应力加速寿命试验的Bayes方法[J].应用数学学报, 1992, 15(3):373-379. [5]程皖民,冯静,周经伦.Weibul1分布产品恒加应力缺失数据下的Bayes可靠性评估[J].电光与控制,2008,15(1):47-50. [6]茆诗松,汤银才,王玲玲.可靠性统计[M].北京:高等教育出版社,2008. [7]汤银才.CE模型下Weibull分布序加试验的Bayes分析[J].系统科学与数学,2006,26(3):342-351. [8]Gilks,W. R.and Wild P. Adaptive rejection sampling for Gibbs Sampling[J].Applied Statistics, 1992,41:337-348.3 Bayes估计
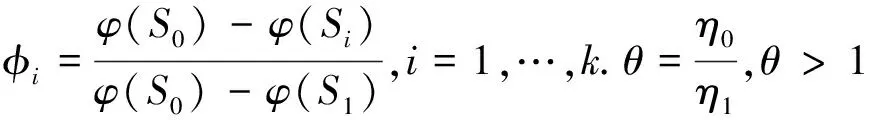




4 仿真例子