矿山地表三维模型实时重建方法的研究
2011-01-23陈晓青任凤玉张国建
陈晓青,任凤玉,张国建
(1.辽宁科技大学,辽宁 鞍山 114044;2.东北大学,辽宁 沈阳 110004)
1 问题提出
虚拟现实技术是计算机图形学领域中发展起来的一种模拟人在自然环境中视、听、动等行为的人机交互技术,在实时仿真领域具有重要的应用。矿山虚拟现实技术涉及大规模复杂虚拟地表模型的动态生成,现代高精度的扫描测绘手段为复杂物体基于多边形网格表示的三维几何建模提供了新的高效手段,但由于采样精度高,由此建立起的三维模型的复杂程度远远超过了当前计算机图形工作站的实时处理能力。
如何降低这些模型的复杂度,减少图形系统需处理的多边形数目,实现复杂虚拟环境的实时快速生成成为研究的关键。
本文通过数据简化、分块处理、闭合多边形提取和闭合多边形快速建立三角网等几个步骤完成矿山大规模复杂虚拟地表模型的动态生成。
2 数据的简化
地表模型主要采用高程数据通过规则格网模型或不规则三角网模型两种方式来表现。
规则格网将区域空间切分为规则的格网单元,每个格网单元对应一个高程值。数学上可以表示为一个矩阵,在计算机实现中则是一个二维数组。算法比较简单,其显示速度取决于网格分辨率,降低分辨率可相应加快速度,但规则格网本身对地貌的特征描述就比较弱,分辨率降低程度受到一定限制。在全分辨率下,对大规模数字地表模型可见网格直接绘制难达到实时的要求。
不规则三角网模型根据区域有限个点集将区域划分为相连的大小各异、疏密不同的三角网,能用更少的空间和时间更精确地表示复杂的表面。特别当地形包含大量特征(如断裂线、构造线)时,能更好地顾及这些特征,从而可以更精确合理地表达地表形态。由于其描述教率高,长期以来受到人们的普遍关注,但由于三角化过程本身的复杂性以及非规则网格拓扑关系的繁杂性,使得各种基于非规则网格模型的自动生成算法难以达到实时。
矿山图纸主要采用等高线来描述高程,利用等高线矢量数据生成地表模型比较直接。
在地形数据量十分庞大时,数据量和要求的精度一直是一对不可调和的矛盾。在实际应用中,特别是在普通PC机实验环境下,为了达到更流畅的实时显示目的,必须以牺牲地表显示的精度为代价。
模型必须在不失真的情况下,先经过一定简化才能满足要求。网格简化算法的实质就是减少模型的点和面,但又要逼近原始网格。
本文采用基于距离和拐点旋转角阈值相结合的简化方法,生成具有一定真实性的简化地表模型,对原始等高线点删除操作的原则为:①累计距离大于某一给定阈值,中间点删除;②遇到拐点时,如果拐点处夹角大于某一给定阈值,该拐点保留。
3 分块处理
地表模型数据往往由上万甚至上百万个数据组成,如果仅凭前一节描述的简化算法,在正常条件下还是很难实现地表模型的实时生成的。
为此,根据矿山开采的特点,首先将模型数据划分成块,分别处理。
当地下开采时,由于地形长期不变化,模型可以预先处理,由于非规则网格模型数据量少,一般采用非规则网格模型,当然也可采用规则网格模型全网格直接绘制。
当采用露天开采时,随着露天矿的生产,地形可能随时发生变化。但由于露天境界外部分基本上是长期不变化的,这样可以将露天矿山地表分成境界线以外和境界线以内两部分分别处理。露天境界以外部分可以预处理,只对境界线以内部分进行实时构网,这样大大减少了实时处理的数据量。由于露天矿地表采用分块处理,就不能采用规则网格模型,只能采用非规则网格模型。
境界内部分又可分为采坑以内和采坑以外两部分,由于采坑以内部分地表已经揭露,等高线需要删除,采场内部结构采用特殊的台阶构网法单独处理,本文不讨论;采坑以外部分是在境界内部分去除采坑后留下的部分,模型的实时处理实质上只是对这部分进行处理,如图1所示。
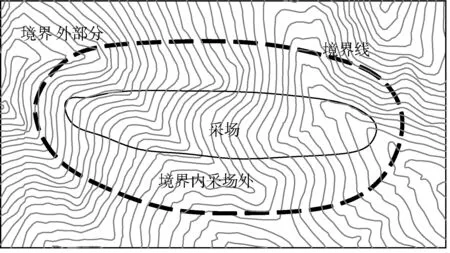
图1 区域分块
4 构建三角网
在简化和分块的基础上,对需要三角化的部分实行三角网的构建。
要实现地表模型的实时显示,就应设计好整个地表网格模型的点、线、面关系,避免复杂的三角化过程。三角化算法是影响实时显示效率的关键。
目前在不规则三角网的各种算法中,大多数是通过三角形的边来扩展新的三角形或在三角形内插入新的点形成三角形,这需要根据很多点或三角形进行判断,从而大大影响了构网速度,不适合矿山大数据量的三角网实时生成。所有这些算法中,Delaunay三角网算法比较有代表,应用也广泛,其算法主要有区域生长法、逐点插入法和分治法三类,这三类方法各有特点。区域生长法思路简单,易于编程,但在搜索“第三点”每次寻找最优点时需要遍历整个点集并比较,往往需要耗费大量的时间;逐点插入法是采用点插入的方式,实现较简单,占用内存较小,但在插入的过程中需要对边界点和边界边进行判断,在时间复杂度上太大,不适合实时生成;分治法综合其它算法,采用递归分割区域进行处理,比较高效,但在合并网的过程中,空间复杂度太大。
本文运用分治法的原理,提出将区域划分为闭合多边形,再对闭合多边形进行三角化,较好地解决了传统算法在构建大数据量不规则三角网时的不足,提高构网速度。
4.1 区域分区
如图2所示,要对该地表区域进行三角化。由图可以看出,整个区域是由等高线与边框线构成的闭合多边形区域组成的,只要能提取这些闭合多边形,直接对各闭合多边形进行三角化即可,这样可以大大降低算法的复杂度,提高三角化速度。
在提取闭合多边形的过程中,经常会出现环形区域,也称为空洞,如图3所示的阴影部分,这给闭合多边形描述增加困难。
为了消除空洞,只需在等高线某点处作竖线或横线,把空洞割成两份即可。这种处理同时也把整个区域划分为若干条区,对每个区实行分治处理,可以大大减少每次三角化时顶点的分析比较次数。
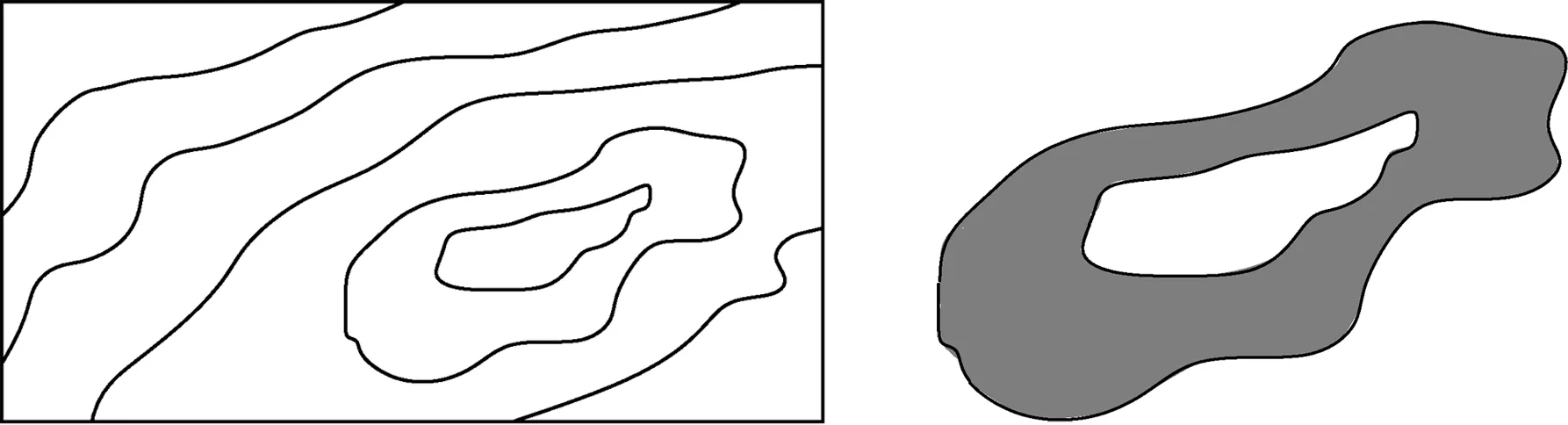
图2 待处理的区域地形 图3 空洞现象
增加分割线,同时也增加了顶点数,因此,应该尽量减少分割线数。具体做法是:先计算区域长轴方向,确定采用竖线或横线进行分割。把每条等高线标记“未处理”,对每条“未处理”的等高线在其起点处作分割线,再把该分割线穿过的等高线标记“处理过”,这样逐条等高线进行处理,直到每条都处理过。如图4所示,采用了两条竖线分割,将区域分为三个区。

图4 分区
4.2 闭合多边形的提取
本文采用多叉树的方法提取闭合多边形。首先计算等高线与边框的交点,图5(a)中1~12数字为交点,以这些交点为节点,构造多叉树。从根节点出发,通过树的遍历,逐个节点进行比较,遇到同一个交点,即构成一个闭合圈,如图5(b)中虚线构成闭合多边形。
4.3 闭合多边形三角网的构建
通过以上闭合多边形的提取,我们可以对闭合多边形进行三角化,算法如图6所示。
取多边形长轴方向(以X方向为例)的中值作竖线,如图6中第1次的竖线交多边形于1~4点。为了不增加额外的顶点,直接在多边形上找离交点最近顶点代替1~4交点作为分割点,这种做法同时也保证了三角形间的无缝拼接问题。通过分割点两两的连线在多边形的内外来判断两两是否作为分割线。如图6中线段23在多边形外,不可作为分割线,而线段12和34在多边形内,可以作为分割线,将多边形分割为三部分。
采用递归法,分别对分割出的各多边形再进行分治,直到该多边形顶点数为3时,直接构成三角形,终止递归。这样完成整个多边形的三角化。
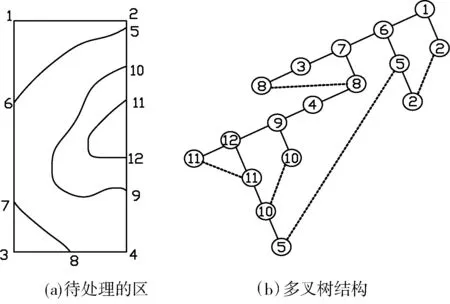
图5 多叉树提取闭合多边形
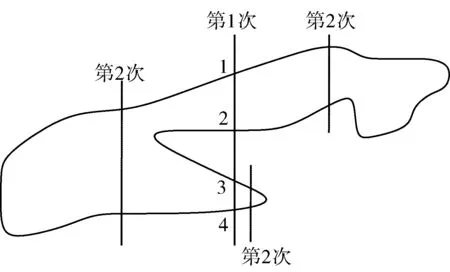
图6 中值递归分治法实现闭合多边形三角化
5 实例
通过以上方法的处理,建立起三角网,在OpenGL支持下,经过模型生成与变换、视点变换、投影变换、纹理生成就可以生成真实感地形。图7为一虚拟矿山地表模型的实例。

图7 一个虚拟矿山实时场景
6 结论
针对矿山开采的特点,本文算法在保证地形正确性的同时,提升了运算速度,能够对大规模地表模型进行有效的实时重构。本文的建模结果已成功地应用到矿山虚拟现实技术的三维构模中。
[1] 谢传节,万洪涛.基于四叉树结构的数字地表模型快速生成算法设计[J].中国图象图形学报,2002,7(4):394-399.
[2] 张凯选,潘梦清,方辉.利用等高线生成DEM方法的研究[J].测绘工程,2007,16(3):15-18.
[3] 翁巧琳,姜昱明.基于等高线的三角网建模及真实感地形重建[J].计算机仿真,2007,24(10):188-191.
[4] 刘学慧,吴恩华.基于图象空间判据的地表模型加速绘制技术。软件学报[J],1998,9(7):481-486.
