主成分聚类分析在矿井安全评价应用中的思考

王德青

(江苏省有色金属华东地质勘查局， 江苏 南京 210007)

在矿山开采过程中，如何对矿井的安全状况进行全面的分析和评价，采取合理的防范措施降低安全风险以确保安全生产，是矿山企业一直关注的热点问题。由于矿山开采是一个复杂的系统，存在的各种风险，有害因素也不尽相同，因此对矿井安全的科学评价关键，在于找到适合不同矿井、不同危险因素的安全评价方法。根据多年的实践和总结，笔者认为，对矿井安全的科学评价需要满足：①从整体出发，在全方位考虑影响矿井开采安全因素的基础上，构建科学的安全评价指标体系；②不断地创新安全评价方法，以适应新的矿井安全评价需要。作为《中国矿业》的忠实读者，笔者一直关注发表在期刊上的关于矿井安全评价文章，如《中国矿业》2009年第2期刊登的论文《主成分聚类分析法在煤矿安全评价中的应用》(以下称《王文》)，提出一种基于主成分因子得分的聚类方法，不妨称作主成分聚类分析。通过相关文献的分析比较，笔者发现，主成分聚类的思想可取，但该方法的理论论证及方法改进有待进一步深化。鉴于以上认识，笔者略作拙文，提出主成分聚类的改进方法，以期与王旭、霍德利两位作者商榷，共同促进矿山安全评价的进步。

1 主成分聚类分析的理论基础及改进

主成分聚类分析，顾名思义即主成分分析和聚类分析的结合使用。主成分分析和聚类分析作为两种基本的处理复杂数据集的数值分类技术,在自然科学和社会科学研究领域均有广泛的应用,并有许多成功应用的例子。尽管这两种方法很有用,但它们都有自己的适用场合和需要满足的条件。如果忽略方法使用的前提条件,盲目地将二者结合使用,不仅不能取得理想的分类效果,反而可能因为错误的分类结果影响决策的正确制定。主成分分析本质上是一种线性变换，其目的是通过线性变换，将原始指标组合成相互独立并能充分反映总体信息的指标，从而在不丢失重要信息的前提下，避开指标间共线性问题，相当于从空间上转换看数据的角度，突出数据变异的主要方向，归纳重要信息。聚类分析是研究“物以类聚”问题的一种统计方法,目的在于使同类对象之间的同质性和不同类对象之间的异质性最大化。但是，当变量存在共线性时，如果直接聚类分析,会放大变量的作用,使得分类结果不科学[1]。由主成分的性质[2]知，主成分变量之间是线性不相关的，因此可以将主成分与聚类分析结合起来，即先做主成分分析，再提取若干主成分对样本进行聚类分析[3]，即《王文》提出的主成分聚类分析。笔者认为，主成分的方差贡献率是递减的，也即主成分的重要性存在差异,而传统的距离公式将参与聚类分析的变量等权对待，不能体现主成分重要性的差异，因此主成分聚类分析的分类结果有待进一步商榷。显然地,如果两个样本第一主成分变量之间相似性，相对这两个样本的其他主成分变量之间的相似性更高,则这两个样本聚为一类的可能性较大。鉴于主成分变量重要性的不同,笔者认为可，赋予不同的主成分变量不同的权重来体现这种差异。因此，《王文》提出的主成分聚类分析可作如下的改进：

(1)加权欧氏距离主成分聚类。如果变量之间是正交的，则欧氏距离有明确的空间距离概念，而主成分公因子之间是正交的，因此改进的主成分聚类分析采用欧氏距离定义样本之间的相似性。但是，主成分公因子的重要性是不同的，第一主成分的方差贡献率最大，因此主成分重要性的差异必须得到体现。本文定义如下的加权欧氏距离公式：

(1)

式中，Fk为主成分公因子；αk为公因子Fk的方差贡献率。下同。

(2)加权主成分因子综合得分聚类分析。由于主成分方法提取的公因子之间信息不重叠，并且每个主成分公因子的重要性由其方差贡献率体现。因此，可以根据各公因子的方差贡献率比重作为权重加权汇总,得出各个样本的综合得分,即:

(2)

将各样本的公因子得分值Fk代入式(1) 、式(2)，以式(1) 、式(2)的计算结果为基础,按传统的聚类分析便可将样本分类。需要说明的是，为了达到数据简化的实际意义，并不需要提取全部的主成分公因子，但当样本之间相似性较高，少数几个公因子不能有效地将样本分类时，需要提取全部的公因子。

改进的主成分聚类分析与传统聚类分析的核心区别，在于考虑了聚类分析过程中常见的变量共线性对分类的强影响；在于最大程度地综合使用剔除共线性、线性化变换、剔除弱影响项等手段，有效降低最终分类模型误差；在于指标的赋权科学、合理。改进的聚类分析，每一步都有充分的理论保证其合理性、必要性，有着同类复杂分类问题下的普遍适应性。

2 各种分类方法的实证比较

2.1 样本选取及数据来源

本文将两种改进的主成分聚类分析方法，用于矿井安全水平的分类问题研究，通过比较新方法的分类结果与《王文》的聚类分析结果，目的在于论证两种改进的主成分聚类分析方法的科学性,解释不同矿井安全水平的差异,以发现安全工作中的盲点。为了最大程度地增强对比的效果,本文直接采用《王文》的数据为处理数据。需要说明的是，本文并未选择全部的7个主成分公因子,而是选取方差贡献率较大的前3个主成分公因子。公因子命名及原始数据如表1所示。

表1 公因子命名及方差贡献率[3]

2.2 数据分析过程

本文使用SPSS(12.0) 统计软件作为分析工具,先对3个主成分公因子原始数据进行标准化处理,然后调用SPSS(12.0)中的聚类分析程序,采用组间联结系统聚类法[3]，分别按加权主成分因子综合得分和加权欧氏距离两种方法进行聚类分析。为了增强可比性,本文亦对矿井进行了直接聚类分析,结果见图1～图3、表2。

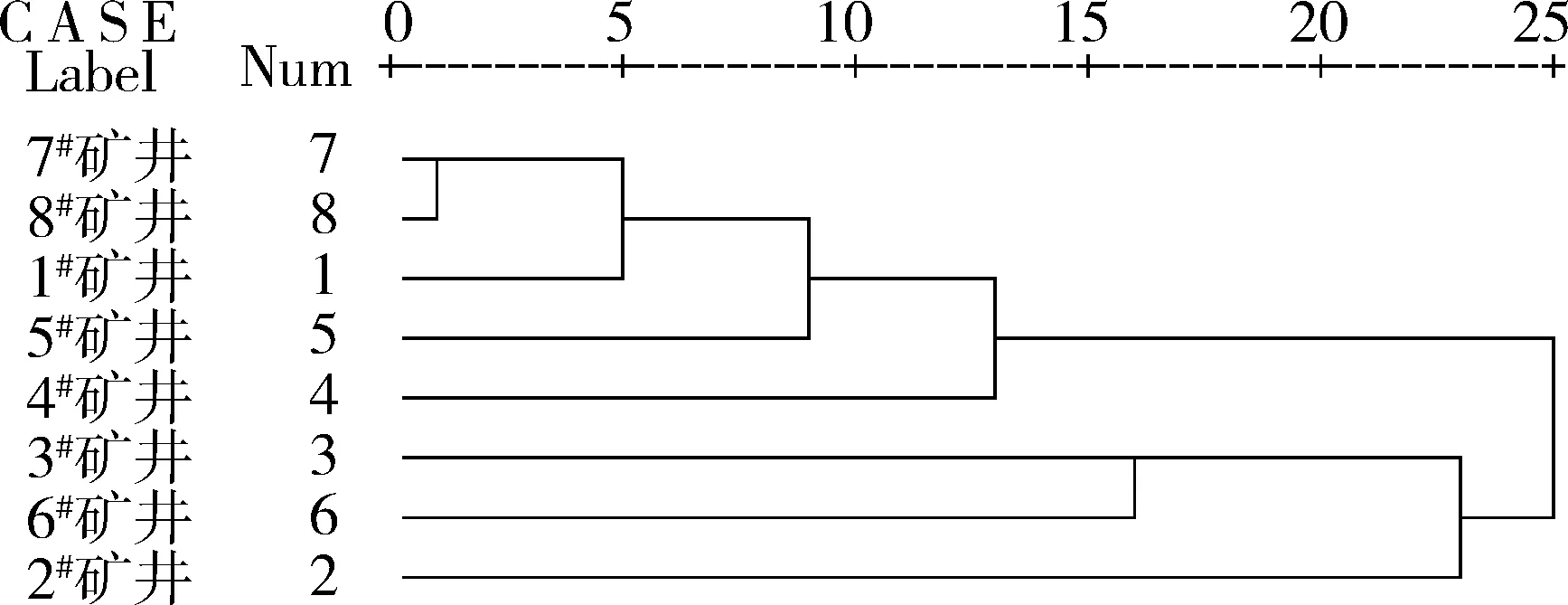
图1 直接聚类分析谱系图

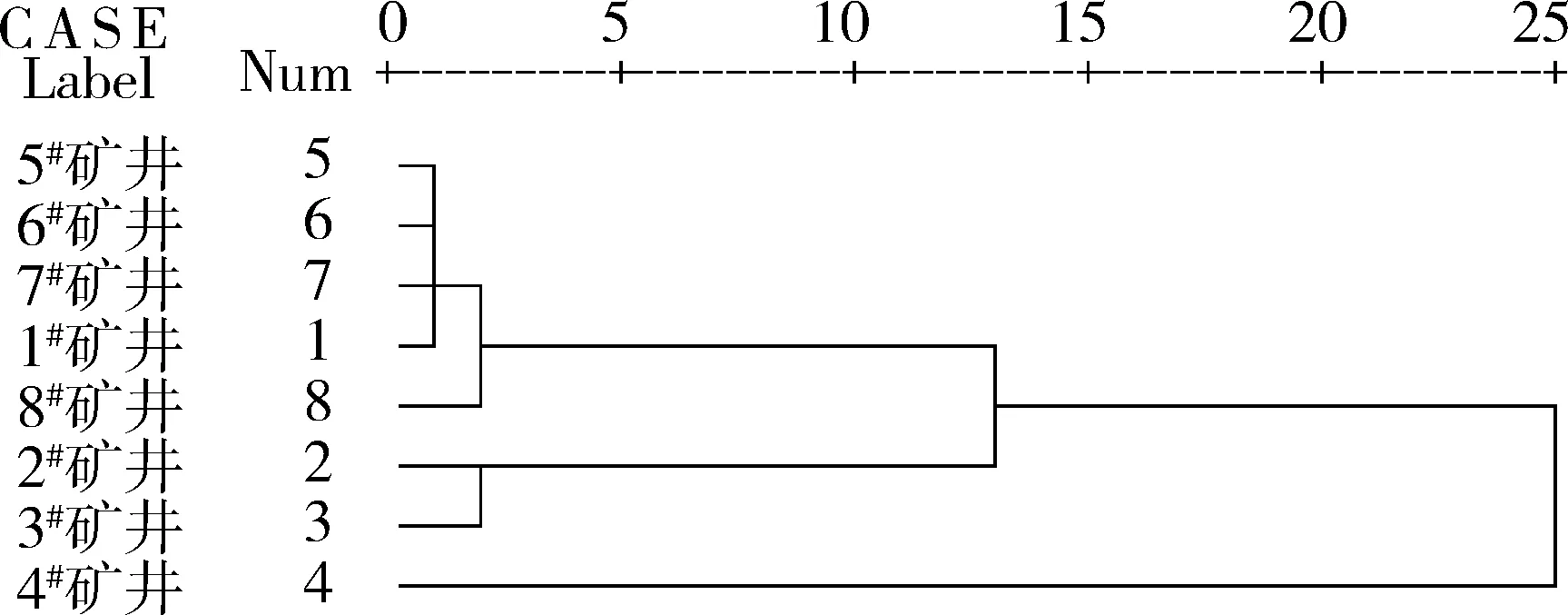
图2 主成分因子综合得分聚类谱系图

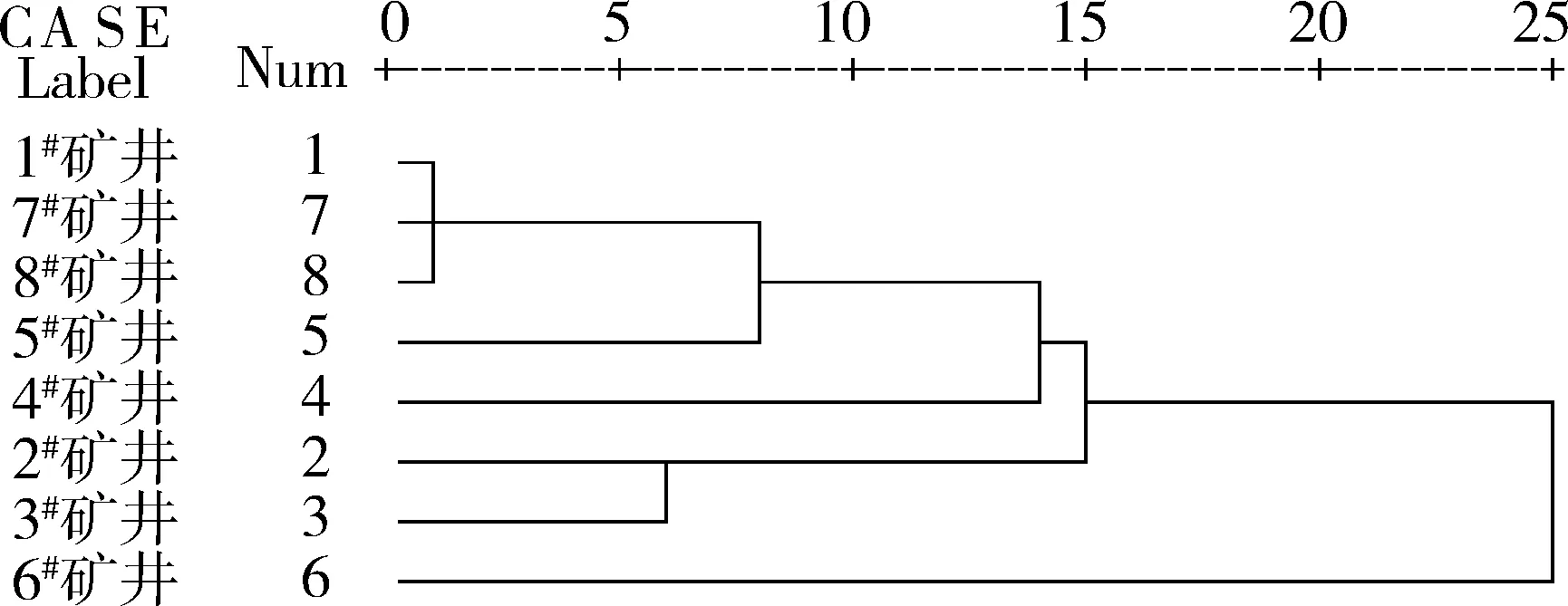
图3 加权欧氏距离聚类谱系图

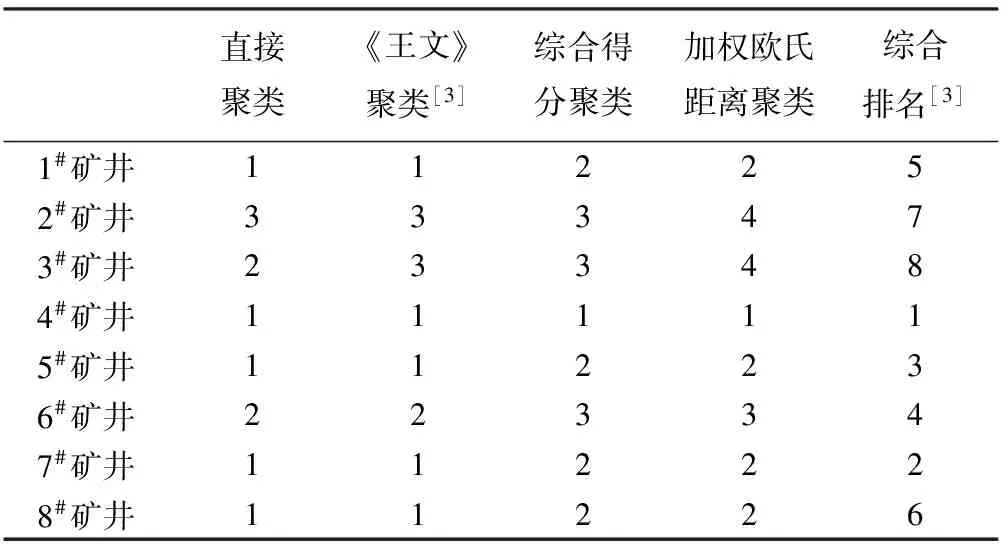
表2 各种聚类方法分类结果比较

2.3 结果评价

基于表2中各种聚类方法的分类结果发现,4种聚类分析的分类结果存在较大差异。图1及表2第一列为直接聚类分析的结果,不难发现,直接聚类分析对矿井的区分度不大,分类效果不佳,难以结合分类结果分析矿井的安全问题。《王文》的分类结果与直接聚类分析的结果相差不大，结合综合排名发现，6#矿井的聚类分析结果排序与其综合排名先后顺序颠倒。图2、图3及表2的四、五两列为两种改进的主成分聚类分析结果。由图2、图3聚类分析谱系图及聚合系数可知，改进的主成分聚类分析对矿井的区分度增强，尤其是加权欧氏距离聚类分析对矿井安全水平差异区分度最大。为了形象地对八个矿井的安全水平进行分析,本文绘制矿井安全水平的雷达图，如图4所示。在绘制雷达图时,为了绘图方便和图示清晰,本文对公因子数据进行了0～1化处理,并添加了间隔轴。

两种改进的主成分聚类分析结果都显示，4#矿井和6#矿井单独成一类。结合这两个矿井的原始指标数据和主成分因子得分数据不难发现，4#矿井的各项指标数据都是八个矿井中最好或接近最好的，特别是4#矿井的自然灾害管理公因子在八个矿井中排名第一，并且与其他矿井的差距较大，领先地位明显。由于自然灾害管理公因子的方差贡献率远大于其他两个公因子，因此4#矿井在此公因子上的领先优势，提升了其在八个矿井安全评价中的排名。尽管6#矿井的F2、F3两个公因子排名都是第一，但是6#矿井的自然灾害管理公因子却排名第六，因此6#矿井是安全管理极不平衡的典型矿山，影响了其安全评价的综合排名。1#、5#、7#、8#矿井为第三类，这四个矿井的三个公因子取值均处于八个矿井中的平均水平，属于各项安全管理比较平衡的矿井。2#和3#矿井为第四类，这两个矿井的公因子取值均是八个矿井中最低或接近最低的，两个矿井的综合排名也是最后两位，属于安全管理落后的典型代表，必须引起管理部门的足够重视。鉴于自然灾害管理公因子的方差贡献最大,体现了矿井安全管理的主要方面,因此,在经济能力受限的条件下,2#、3#和6#矿井应集中主要精力加强自然灾害安全方面的管理,这也是抓住了工作的重心。

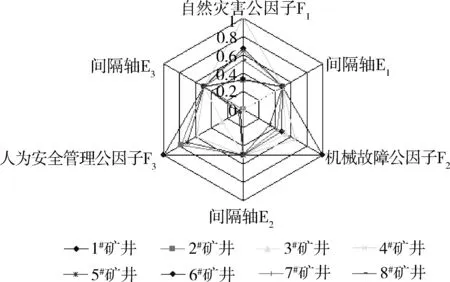
图4 矿井安全水平主成分得分雷达图

3 结语与建议

矿井安全评价是以安全系统工程理论为基础，合理选择评价方法，对矿井已经存在和潜在的危险有害因素进行识别和分析，并提出合理可行的安全技术和安全管理对策措施的系统工程，目的是把生产过程中的不安全因素和作业场所的隐患消灭在萌芽阶段。由于同一类事物之间具有更多的近似特性,分门别类地进行研究,要远比在一个复杂多变的集合中更清晰明了。因此，科学地

将不同类型的矿井分类，不仅大大减少了安全评价数据处理的工作量，而且可以准确发现危险因素所在，及时地为安全生产管理和决策提供合理的参考依据。

矿井的安全评价，是一项动态的、复杂的系统工程，安全评价的数据分析量大、不确定因素多。基于传统统计技术建立的聚类分析假设条件较多，实际应用中面临诸多的局限，因此对传统聚类分析的改进是迫切需要解决的问题。尽管主成分聚类分析克服了传统聚类分析无法处理共线性变量的缺点,但主成分聚类的距离公式等权对待主成分公因子,不能体现主成分重要性的差异。本文提出的两种改进方法,弥补了主成分聚类指标赋权不科学的不足。实证分析表明,改进的主成分聚类相对原始的主成分聚类分类效果更佳,理论更充分。但是，强调对传统聚类方法的改进，并不是说传统聚类分析方法不重要。应该注意到，传统聚类分析无论是理论推导还是实际应用方面都是比较成熟的，当矿井安全评价数据满足传统聚类方法的条件时，分类问题应该首选传统聚类方法。

[1] 朱建平.应用多元统计分析[M].北京：科学出版社，2006.

[2] 何晓群.多元统计分析(第二版)[M].北京：中国人民大学出版社，2008.

[3] 王旭，霍德利.主成分聚类分析在煤矿安全评价中的应用 [J].中国矿业，2009，18(2)：86-89.

[4] 王德青.统计分类方法的比较 [J].中国统计，2008(9)：44-45.

[5] 汪文雄，等.基于因子与聚类分析的中国建筑业产业竞争力研究 [J].数理统计与管理，2008，27(2)：329-337.

[6] 王庆丰，等.基于因子与聚类分析的县域经济发展研究 [J].数理统计与管理，2009，28(3)：495-501.

[7] Sharma S. Applied Multivariate Techniques [M].John Wiley & Sons,Inc.,1996.