有色金属价格指数关联性的VAR分析

方 兰，沈 镭

(1.中国科学院地理科学与资源研究所,北京100101;2.兰州银行股份有限公司，甘肃 兰州 730030)

上海有色金属价格指数(SMMI)，选择了产量占全国有色金属总产量90%以上的铜、铝、铅、锌、锡、镍六个有色金属品种为代表品种，指数的采标涵盖了中国铝业、江西铜业等100多家行业内主要企业。采用了加权调和平均数法和交叉权数法编制，能够较为客观、真实地及时反映国内有色金属市场的运营状况、景气程度、价格的总体走向，被认为是有色金属市场风向标，甚至有学者指出其拥有定价权之作用。出于对数据保存的最大化及稳健性考虑，本文选取2009年以来每周五公布的SMMI，对国内铜、铝、铅、锌、锡、镍六个有色金属市场进行研究。以分析上述六个有色金属市场间，是否存在着长期稳定的均衡关系、一个市场价格波动对其他市场是否将产生影响，以及产生的影响是否显著。

1 价格指数的联动特性

上海有色金属价格指数(SMMI)，包括SMMI、SMMI-Al、SMMI-Cu、SMMI-Ni、SMMI-Pb、SMMI-Sn、SMMI-Zn六项，分别对应铝、铜、镍、铅、锡、锌六个有色金属品种(为简化起见，下文模型中简称为Al、Cu、Ni、Pb、Sn、Zn)。根据运算的连续性、可比性与一致性要求，对中国钼业证券市场研究的数据样本区间为2009年1月1日至2010年7月2日，遴选出每周五的六项有色金属价格指数，并以对日原则将任一处数据空白的日期剔除(图1)。

由图1可见，以分项价格指数代表的六个有色金属市场价格波动态势并不近似。通过运用偏度-峰值比较，对上海有色金属价格指数序列进行分析，计算出SMMI-Pb、SMMI-Sn序列峰值均小于2，说明其分布形态相对于正态分布是平坦的，具有低峰、薄尾的特征；反之， SMMI-Al、SMMI-Cu、SMMI-Ni、SMMI-Zn序列峰值均大于2，说明其分布的凸起程度大于正态分布，具有尖峰、厚尾的特征。此外，除SMMI-Sn序列外，其余序列偏度均为正，其右向尾部比左向尾部更长。当上述六种有色金属之间相互独立时,市场价格可被视为是大量独立随机事件的总合，即其波动应服从高斯分布，而这种非高斯分布，说明了上述六种有色金属价格波动相互独立或弱相关的假设并不成立。 铝、铜、镍、铅、锡、锌金属价格之间的联动性，是有色金属市场结构本身具有的特性之一。上海有色金属价格指数序列描述性统计结果见表1。

图1 上海有色金属价格指数序列图较

表1 上海有色金属价格指数序列描述性统计结果

2 VAR模型建立与脉冲函数分析

为了具体分析铝、铜、镍、铅、锡、锌金属价格波动之间相互影响的程度，本文在向量自回归模型(Vector Auto Regressive Model，简称VAR模型)基础上，研究其动态特性。向量自回归模型以数据本身来确定模型的动态结构，是一种非结构化的多方程模型，通常用于相关时间序列系统的预测和随机扰动对变量系统的动态影响分析，且不需要对变量的内生性和外生性进行假定，即可以将向量自回归模型中所有的变量都看作是内生的。

在一个含有n个被解释变量的VAR模型中，每个被解释变量都对自身以及其余被解释变量的若干期滞后值回归，令滞后阶数为k，则向量自回归模型的一般形式为

Yt=A0+A1Yt-1+…+ApYt-p+εt

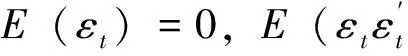
六个方程的检验结果表明,其均有较好的拟合效果。向量自回归动态方程系数估计见表2。向量自回归动态方程整体检验结果见表3。

向量自回归模型中的内生变量共同组成了封闭系统，但其单个参数估计值的经济意义并不明确，应借助脉冲响应函数(Impulse Response Functions，IRF)等衡量来自随机扰动项的一个标准差冲击对内生变量当前值和未来值的影响。

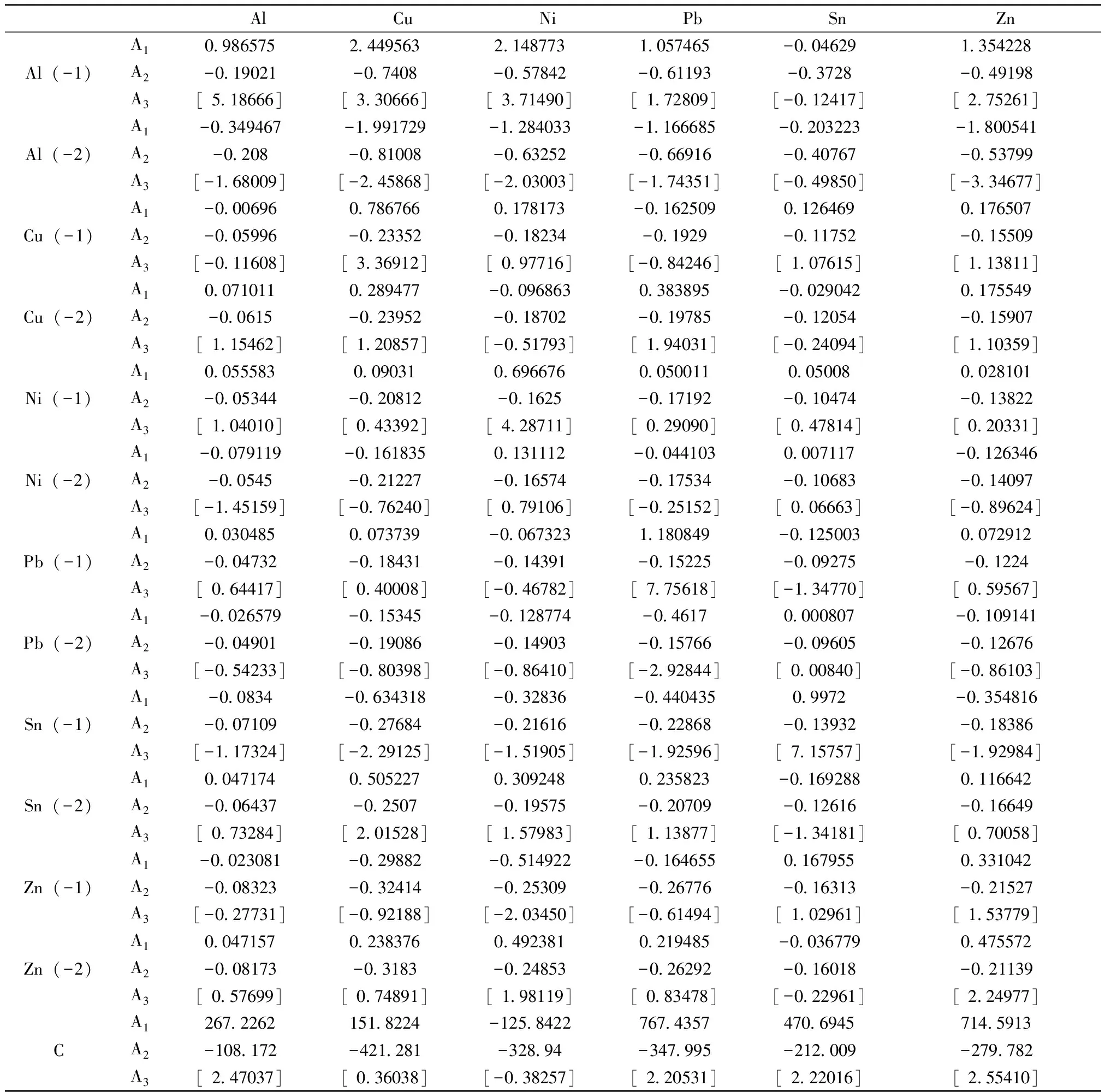
表2 向量自回归动态方程系数估计

表3 向量自回归动态方程检验结果

设有双变量一阶向量自回归模型VAR(1)如

Qt=α11Qt-1+α12Mt-1+ε1,t，Mt=α21Qt-1+α22Mt-1+ε2,t

其中，Q和M是VAR(1)中的内生变量；ε是随机扰动项。在VAR(1)中，因Q的滞后项在两个方程中都是解释变量，ε1,t发生变化会立刻改变Q的当前值，也会通过当前的Q值影响到变量Q和M今后的取值。脉冲响应函数就是试图描述这些影响的轨迹，显示任意一个变量的扰动如何通过模型影响所有其他变量，最终又反馈到自身的过程。常引入一个变换矩阵Z与信息εt相乘，使Vt=Z·εt～(0,Ω)，把εt的协方差矩阵变换为一个对角矩阵，将脉冲响应函数绘制成脉冲响应曲线图，则可以更直观地分析冲击对每个内生变量的动态影响。如果脉冲响应曲线趋于零，说明一变量暂时波动，对另一变量没有持久影响；如果趋于某一数值，则说明一变量暂时波动，对另一变量有持久影响；如果脉冲响应曲线位于零坐标线上方，即显示一变量暂时波动，可引起另一变量同向变化；若曲线位于零坐标线下方，则表示一变量暂时波动，可引起另一变量反向变化。

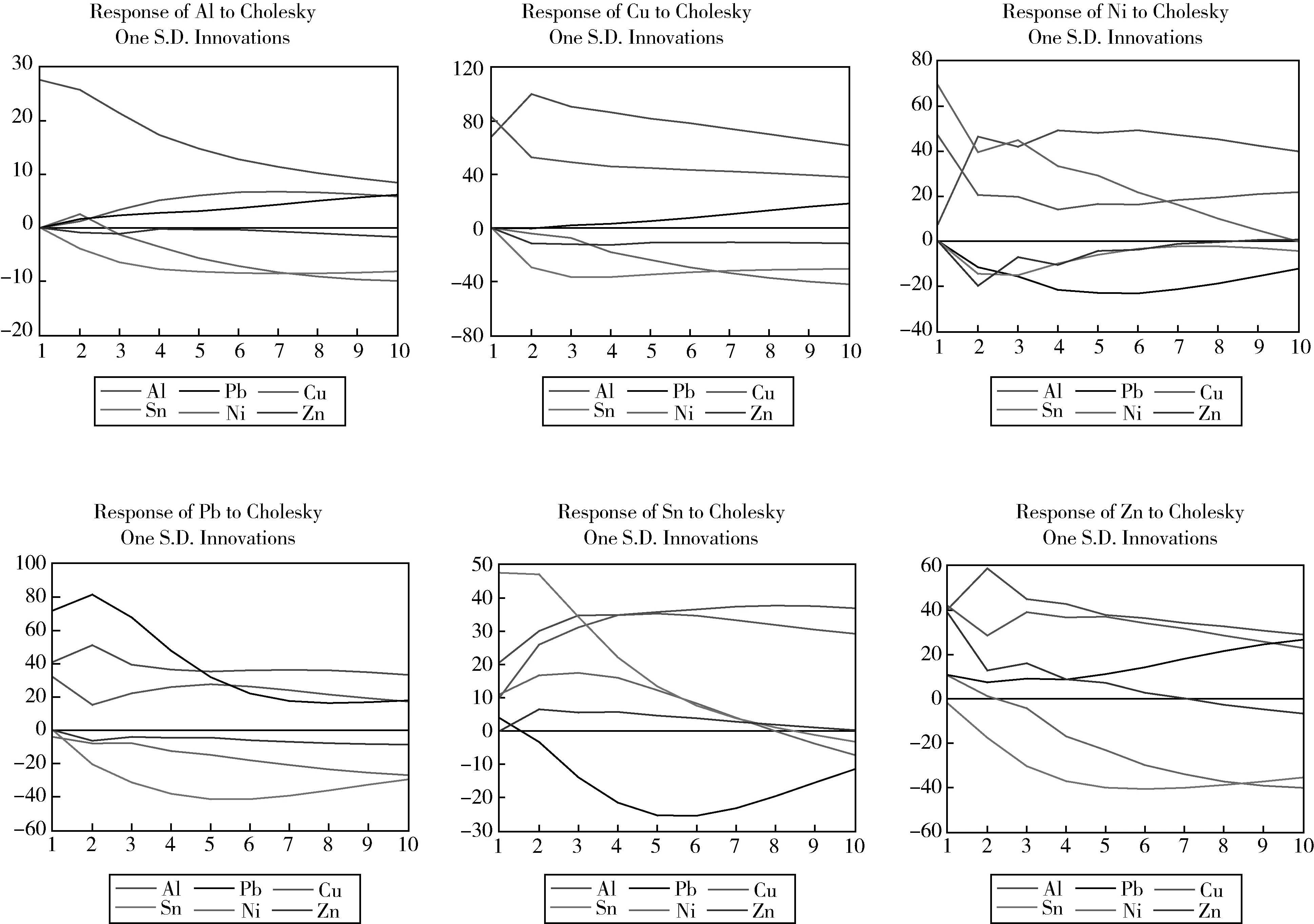
图2 脉冲响应曲线(10期)

图2清晰地揭示了铝、铜、镍、铅、锡、锌金属价格波动之间相互影响的程度与时滞：铝金属价格受其他金属价格扰动后，当即产生正向波动，铜影响最为显著；铅、锌影响基本持平，次于铜；而锡、镍对其影响仅分别为铅、锌影响的1/2与1/4左右。铝金属价格一个标准差扰动，引起其余五种金属价格变化时滞约为1期，其中，锌金属价格受铝金属价格扰动较小；铜、铅金属价格受扰动后产生正向波动；锡金属价格受扰动后2期内为正向波动，随后为反向波动；镍金属价格受扰动后产生反向波动。铜金属价格受镍、铅、锡、锌金属价格扰动后，当即产生正向波动，影响幅度依次为镍、锌、铅、锡。而铜金属价格一个标准差扰动，引起这四种金属价格变化时滞也约为1期，其中镍、锡、锌金属价格受扰动后产生反向波动，铅金属价格受扰动后产生正向波动。镍金属价格受铅金属价格扰动后当即产生反向波动，受锡、锌金属价格扰动后当即产生正向波动，影响幅度依次为锡、锌、铅。镍金属价格一个标准差扰动，引起除铝、铜金属价格当期变化，引起其余四种金属价格变化时滞也约为1期。铅金属价格受锡、锌金属价格扰动后，当即产生正向波动，锌较锡影响力更高。铅金属价格一个标准差扰动，

引起锡、锌金属价格变化时滞约为1期，并引起镍金属价格当期反向变化。锡、锌金属价格扰动对彼此的影响时滞约为1期。

3 结论与讨论

借助基于向量自回归模型构建的脉冲响应函数，对2009年1月1日至2010年7月2日之间的铝、铜、镍、铅、锡、锌金属价格波动进行研究，可以得出结论：就价格的总体影响力或引导力而言，由强至弱分别为锌、锡、铅、镍、铜、铝；而就具体金属品种而言，铝金属价格最易受其他金属价格扰动而波动。六个有色金属市场间，的确存在着长期稳定的均衡关系，一个市场价格波动对其他市场将产生显著的影响，其间时滞是短暂的。未来应在此基础上，进一步健全完善价格监测体系，密切监测有色金属市场价格变化，加强对有色金属价格波动的预警工作，更好地服务于经济社会发展。

[1] 史爱萍. SMMI谋求有色金属定价权[J]. 上海有色金属，2007(03)．

[2] William Greene. Econometric Analysis. Third Edition Prentice Hall,1997．

[3] 孙敬水．计量经济学教程[M]．北京：清华大学出版社，北京交通大学出版社，2005．

[4] Sims,Christopher A． Macroeconomics and Reality,Econometrica,Econometric Society,1980,48(1).

[5] Kincho H.Law,David R.Mackay,A parallel row-oriented sparse solution method for finite element structural analysis. International Journal for Numerical Methods in Engineering,1993，36．