一种混合属性数据的聚类算法

张艳丽，郑 诚

（安徽大学 计算机科学与技术学院，安徽 合肥 230039）

一种混合属性数据的聚类算法

张艳丽，郑 诚

（安徽大学 计算机科学与技术学院，安徽 合肥 230039）

提出一种基于属性分解的随机分组的改进方法，以提高聚类算法的稳定性和适用性。实验仿真结果表明，改进算法具有很好的稳定性和应用性。

聚类；混合数据；分类属性

所谓聚类，就是将物理或抽象对象的集合构成为由类似的对象组成多个类或簇的过程。由聚类所生成的簇是一组数据对象的集合，同一簇中的数据对象尽可能相似，不同簇中的数据对象尽可能相异[1]。聚类算法在许多领域获得了广泛应用[2]，但是，由于在实际应用中，许多数据集不仅包含数值属性的数据，同时也包含如地图颜色、几何纹理等分类属性的数据。因此使得基于传统的欧式距离划分的聚类算法难以适用于混合属性数据集的要求。为此各研究学者就此问题进行了深入地研究和探讨。

MacQueen所提出的 k-means方法[3]是最早、也是最简单的聚类方法，但是该方法只能对数值属性的对象集进行聚类，无法对分类属性和混合型属性的对象集进行聚类。Huang提出的k-modes算法和k-prototypes算法[4]推广了k-means方法，使之可以对分类属性和混合型属性的数据集进行聚类。同时陈宁、陈安、周龙骧进一步提出了模糊k-prototypes算法，并利用引进模糊聚类算法来提高聚类结果的准确性[5]。

上述方法在聚类过程中，均利用分类型属性简单匹配相异度，将分类型属性的数据转化为数值型属性数据间的基于距离的计算问题，从而解决了对混合属性数据集的聚类问题。但是上述方法在对分类属性数据和混合型属性数据进行聚类时，总会存在一些如聚类结果的随机性和不稳定性等缺点，甚至有时会出现空聚类[6-7]现象。

为此，本文在k-prototypes算法的基础上进行改进，利用随机分组的思想动态地选取初始原型点，同时对分类属性数据采取属性分解的方法进行处理，从而提高算法的稳定性和适用性，使聚类结果更加理想化。

1 相关观念

聚类是将数据对象分成类或簇的过程，使同一个簇中的对象之间具有很高的相似度，而不同簇中的对象高度相异[2]。其中对象间的相异度度量用来表示对象间的相异程度，代价函数用来表示对象间的相似程度。

1.1 相异度度量

对象X、Y的相异度定义为对象中不相等的分类属性值的数目。设X、Y是数据集中两个包含m种分类属性的数据对象，也可以说X、Y是数据集中任意两个具有 m（x1，x2，x3，…，xm）维分类属性值的数据对象，对象间的相异度 d（i，j）定义为：

如果xif或者 xjf缺失（即对象 i或对象 j没有变量 f的度量值），或者 xif=xjf=0，且变量 f是非对称的二元变量，则指示项=0；否则，指示项=1。为了方便计算，假定每一个属性中的全部属性值以同等概率出现，即式（1）中的指示项=1。由此得到简化的相异度公式为：

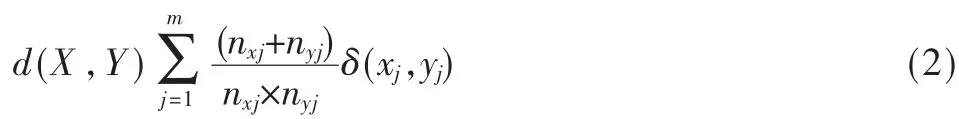
其中，当xj=yj时，δ（x，yj）=0；当 xj≠yj时 ，δ（xj，yj）=1。 nxj，nyj是数据集中属性j所包含属性值xj，yj的个数，举例如表1所示。

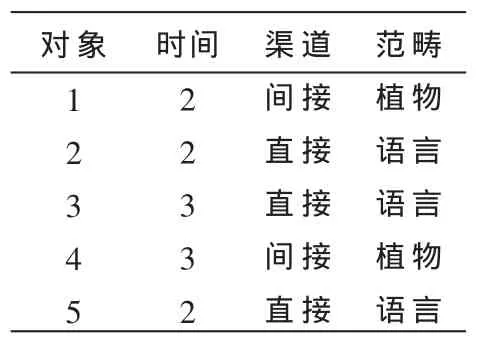
表1 举例所用数据

根据公式计算：d（1，2）=2+2=4；d（1，4）=0；d（1，3）=2+2=4；d（1，5）=2+2=4。

该公式说明两个对象不相等的分类属性值的数目越大，则两个对象越不相似。

由此可以得出，计算数值型数据和分类型数据的混合数据的相异度度量的距离为：

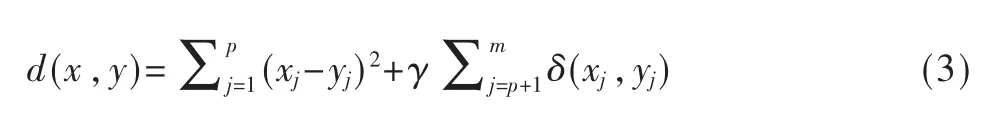
1.2 代价函数的计算

代价函数用来表示对象间的相似程度，扩展kmeans算法代价函数的计算方法，使其可以计算数值型数据和分类型混合属性数据对象的代价函数。定义X是具有m种属性值总数为n的对象的数据集，即X={X1，X2， … ，Xn}，Xi=（x1，x2， … ，xm）， 其 中 包 含 m1个 数 值型的数据，m2个分类型的数据，m=m1+m2，k是正整数，表示聚类的个数。则代价函数的计算总公式为：

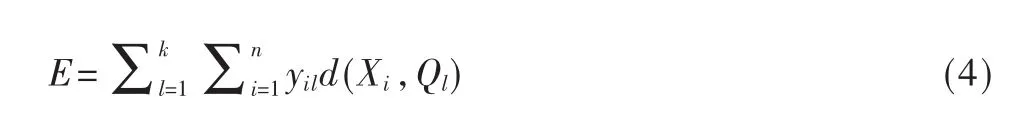
其中，Ql=[ql1，ql2，…，qlm]是聚类 I的模式或者原型，yil是划分矩阵Yn×l中的任意一个元素，d表示相似度量值。在该公式中，Y有以下两个特性：

在式（4）中，针对于混合属性的数据，引用了混合属性数据中的数值属性数据和分类属性数据的计算相异度的式（3），得到总的代价函数公式为：

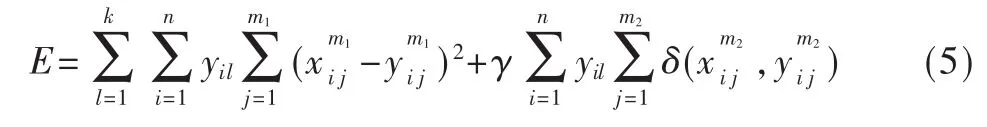
2 算法的改进

k-modes算法和k-prototypes算法在聚类混合属性数据时，对初值有明显的依赖，导致聚类结果不理想，甚至出现聚类空集的现象。因此本文在原有算法的基础上进一步改进，利用随机分组确定初始原型的方法，然后对随机分组得到的初始原型进一步加工处理，使得聚类结果对初值的依赖性有所降低，从而使聚类结果更合理、稳定，达到改进算法的目的。

2.1 分类属性处理算法

假定数据对象x是具有m维属性的数据对象，其中含有m1个数值型数据和m2个分类型属性。那么，可以直观地将数据对象x看成分别有m1维数值属性和m2维分类属性组成，其中m2维分类属性又可以分别看成由多维数据值组成。例如：表2中的分类型属性“渠道”可以看成是由 “直接”、“间接”2维分类数据值组成的；分类型属性“语义范畴”可以看成是由“植物”、“语言”2维分类数据组成的。在计算中，分别将分类型属性看成是由多维的分类属性数据值组成的。

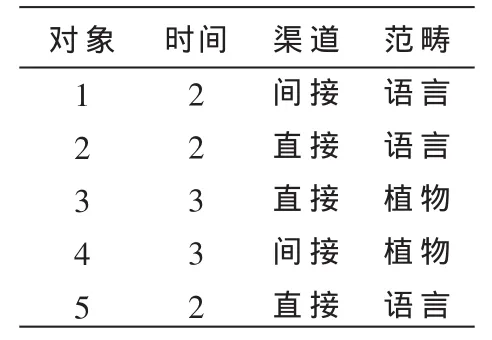
表2 属性分解原型举例

对象1的分解原型表示为：

1={2，{0（直接），1（间接）}，{1（植物），0（语言）}}；

对象2的分解原型表示为：

2={2，{1（直接），0（间接）}，{0（植物），1（语言）}}；

对象3的分解原型表示为：

3={3，{1（直接），0（间接）}，{1（植物），0（语言）}}；

对象4的分解原型表示为：

4={3，{0（直接），1（间接）}，{1（植物），0（语言）}}；

对象5的原型表示为：

5={2，{1（直接），0（间接）}，{0（植物），1（语言）}}；

则对象1，2，5组成的聚类Q1的分解原型可以表示为：

Q1={2，{2/3（直 接 ），1/3（间 接 ）}，{0（植 物 ），3/3（语言）}}；

则对象3，4组成的聚类Q2的分解原型可以表示为：

Q2={2，{1/2（直 接 ），1/2（间 接 ）}，{2/2（植 物 ），0（语言）}}；

然后利用式（2）计算对象与聚类之间的距离，得到其中的最小距离。通过这种方式，可以有效地避免在分类属性中出现频率少的属性值丢失的现象，从而得到更合理的聚类的结果。

2.2 随机分组算法

随机分组算法的基本原理是依据需要聚类的个数k和数据集中所包含数据的个数n。将总数为n的数据集划分为count=n/k组，然后从count组中分别选择数据对象k次，构成k个聚类的初始原型值。

算法流程：

（1）分组数据集。已知数据集 X={x1，x2，…，xn}是包含n个数据对象的集合。依据数据集中数据个数n和需要聚类的个数k，将整个数据集分组成为count=n/k组，即数据集 X={[x1，x2，…，xk]，[xk+1，…，x2k]，…}。 如果分组后数据集中还有剩余的对象未分配，则将剩余的对象分配到任意组中，本文选择将其分配到第一个分组中。

（2）随机获得一个初始点。将数据集分组成为子数据集后，依次从count个子数据集中随机选择一个数据对象，形成由count个数据对象组成的新的子数据集。将这个新的子数据集中的所有m1个数值型属性中的值利用式（5）计算平均值作为初始点的对应的数值型属性的值，对于分类型属性的值，则利用2.1节的分类属性数据处理方法进行处理后作为初始值的对应分类型属性的值。

（3）重复步骤（2）k次，得到k个初始点，作为聚类分析的k个原型点。

2.3 聚类算法描述

改进算法的流程和k-prototypes算法的流程基本相同。具体算法描述如下：

（1）将数据集中的每一个数据对象按照2.1节中的分类属性数据值的处理方法进行处理。

（2）利用随机分组算法获得k个初始原型点，每一个初始原型点对应一个聚类原型初值。

（3）将数据集中剩下的任一个对象分配给一个聚类，根据相异度度量的距离公式计算的结果确定一个聚类的原型与它最近，分配给该聚类后，将聚类的原型更新。

（4）在所有的数据对象全部分配给聚类之后，重新计算该数据对象与当前每一个聚类之间的距离。如果发现一个数据对象它的最近原型属于另一个聚类而不是当前的聚类，将该数据对象重新分配给另一个聚类并更新两个聚类的原型。

（5）重复算法（4），直到数据集中的所有数据对象再没有对象变更聚类为止。

3 实验分析

一般评价聚类结果均是采用“误分率”等统计方法。在本文的仿真实验中，通过将本文的改进算法和kprototypes算法进行比较，采用错误的分类数目来评价聚类算法性能。错误的分类数目，即对算法的聚类结果和数据集本身进行比较，聚类结果中没有被正确分配到相应聚类的数据对象的数目。本文通过两个数据集进行实验。

（1）采用UCI数据集中的abalone数据集进行测试。该数据集包括涉及生活领域的8个类别的4 177个数据对象，其中含有1个分类型属性，1个整数型属性和6个实数型属性。分类属性数据对象中含有1 528个记录为F（父）值，1 307个记录为M（母）值，还有1 342个记录为I（未成年人）值。

如图1所示，在改变聚类个数的情况下，通过比较两种算法的聚类结果的错误分类数目可知，改进算法在一定程度上比原有算法的稳定性更高。

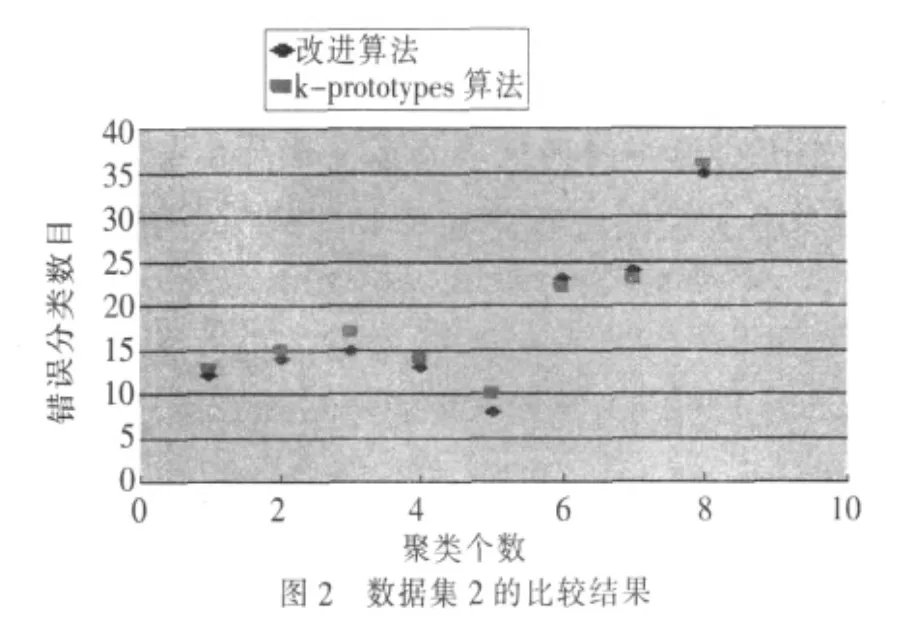
（2）采用UCI数据集中的post-operative patient数据集。该数据集中还有涉及生活领域的9个类别的90个数据对象，其中还有8个分类属性和1个整数型属性，包含有2个记录为I（病人送加护病房），24个对象为S（病人准备回家），64个对象为A（病人送去普通病房）。

由图2可知，在分类属性较多的混合属性数据集中，改进算法的稳定性仍在一定程度上优于原型算法，保证了改进算法对于混合属性数据聚类结果的稳定性和有效性。

对于数值型数据和分类型数据的混合数值的聚类，目前虽然有一些算法，如k-modes算法和k-prototypes算法。但是这些算法在选择聚类初始点时过于随机，导致聚类结果不理想。因此本文提出了一种基于分类属性数据分解的随机分组选择初始原型的改进算法。但是在本文的改进算法中，仍然存在一些缺点，例如，聚类个数仍是人为确定，不能动态确定适合数据集合理的聚类的个数。因此，为了使改进算法的适应性和稳定性更好，同时使数据集的聚类结果与输入数据对象的顺序无关，动态确定聚类合理的聚类个数是今后的研究重点。

[1]王欣，徐腾飞，唐连章，等.SQL Server2005数据挖掘实例分析[M].北京，中国水利水电出版社，2008.

[2]Han Jiawei，KAMBER M.Dataminingconceptsand techniques[M].北京：机械工业出版社，2001.

[3]CHRISTOPHER J，BURGESC.A tutorialonsupport vector machines for pattern recognition[J].Data Mining and knowledge Discovery，1998：2（2）：121-167.

[4]VAPNIK V N.An overview of statistical learning theory[J].IEEE Trans on NeuralNetwork， 1999； 10（5）：988-999.

[5]张文生，王珏.利用支持向量机构造函数型连接网络的研究[J].计算机科学，2001，28（5）：172-177.

[6]赵立江，黄永青.混合属性数据聚类初始点选择的改进[J].广西师范大学学报：自然科学 报，2007，25（4）：102-105.

[7]林培俊，王宇.对类属性和混合属性数据聚类的一种有效地算法[J].计算机工程与应用，2004，40（1）：190-191.

A cluster algorithm of categorical attribute data

Zhang Yanli，Zheng Cheng

（Computer Science and Technical Institute，Anhui University，Hefei 230039，China）

This article proposed a kind of the stochastic grouping improvement method which decomposes based on the attribute，enhances the cluster algorithm the stability and the service ability.The experimental simulation result indicated that，the improvement algorithm has the very good stability and the utility.

clustering；mixed data；categorical attribute

TP301

A

1674-7720（2011）03-0064-03

2010-07-12）

张艳丽，女，1982年生，在读硕士，主要研究方向：数据挖掘，聚类。

郑诚，男，1964年生，副教授，硕士生导师，主要研究方向：数据挖掘，语义 WEB。