基于最小二乘法的工作面上隅角瓦斯浓度分析方法研究

李红晓，汤友谊

(1. 河南理工大学资源环境学院，河南 焦作 454000；2. 河南省煤层气开发利用有限公司，河南 郑州 450016)

目前我国的国有重点煤矿中，49.8%是高瓦斯和突出矿井。在这些矿井中，工作面上隅角的巷道为直角转弯，风流在此容易形成涡流，并且此处是采空区漏风的交汇处，易形成工作面上隅角瓦斯积聚。当遇到高温热源时，就会造成瓦斯爆炸，从而造成人员伤亡和财产损失。

为了控制上隅角瓦斯积聚，实践中一般是采取每日对上隅角瓦斯进行监测，当测得瓦斯浓度超过允许界限时便采取一定的防治上隅角瓦斯积聚的措施，如：在工作面上隅角附近设置木板隔墙或帆布风障；将回风巷道后的联络眼的密闭打开，并在工作面回风巷中设置调节风门或挂风帘，迫使一部分风流经上隅角后由采空区经联络眼排除等措施[1]。在分析研究上隅角气体变化规律时，经常需要分析大量规律性不强的数据，一般难以通过观察预测气体未来变化趋势，需要找到一种方法来拟合和分析数据的变化趋势。最小二乘法可以较好地对上隅角瓦斯气体变化规律进行理论分析和拟合，拟合结果对防治工作面上隅角瓦斯积聚具有指导作用。

1 数据分析模型

在科学实验的统计方法研究中，往往要从一组实验数据(xi,yi)(i= 1,2,…,n)中寻找出自变量x和因变量y之间的函数关系y=φ(x)。由于观测数据不够准确，并不要求y=φ(x)经过所有的点(xi,yi)，只要求在给定xi上误差δi=φ(xi)-yi按照某种标准最小。通常采用欧氏范数‖δ‖2作为误差量度的标准，这就是最小二乘法。在选择了曲线的数学模型之后，使用最小二乘法求取曲线方程中的待定系数，一般通过对偏差的平方和对每个待定系数求偏导数，使偏导数为零，来建立方程组[2]。

1.1 最小二乘法多项式拟合过程

实践中得到一组数据(xi，yi) (i=1, 2,…,n)时，常会遇到因变量y与自变量x之间根本不存在线性关系。此时可以考虑用一个次数低于n-1次多项式[3]

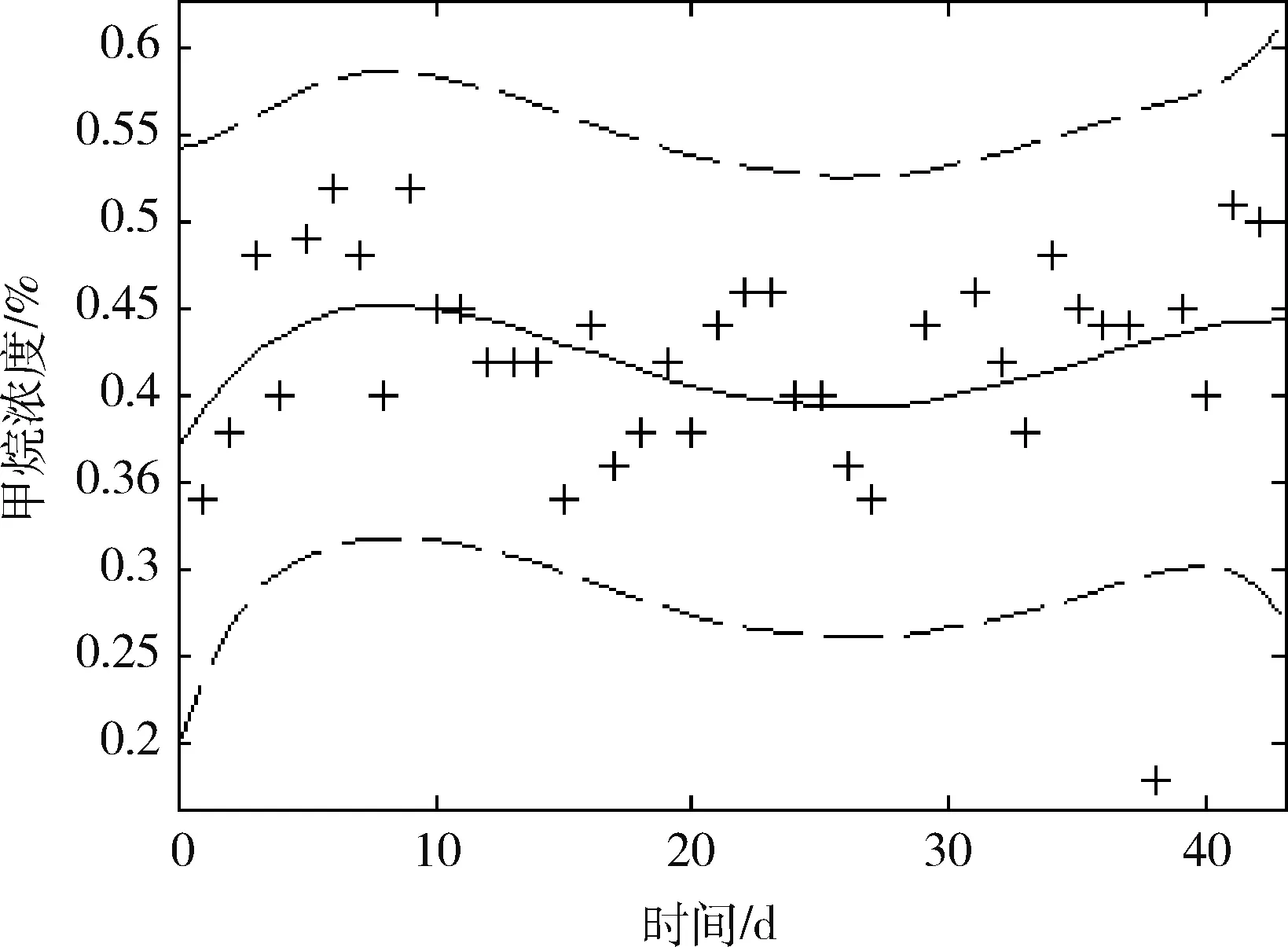
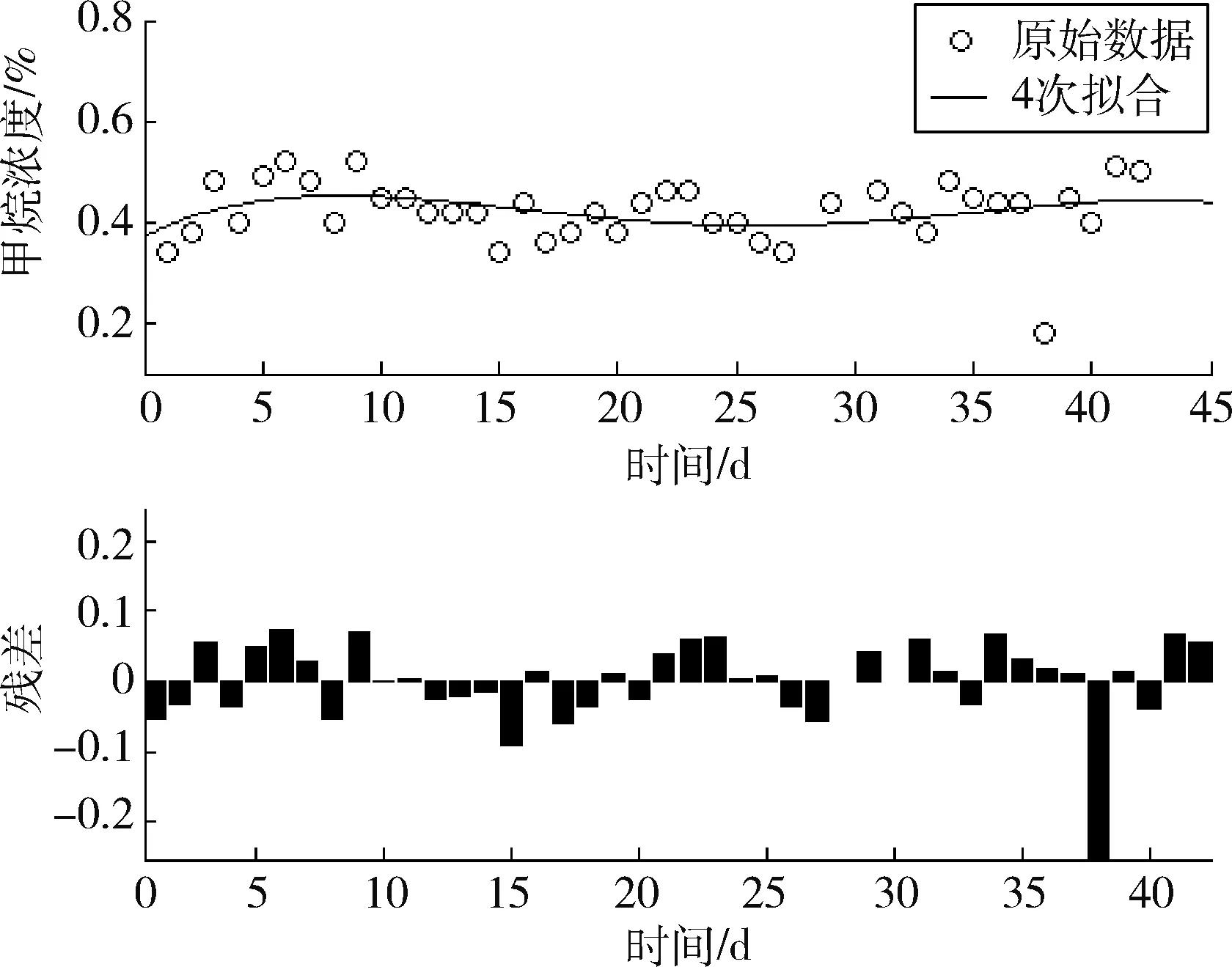
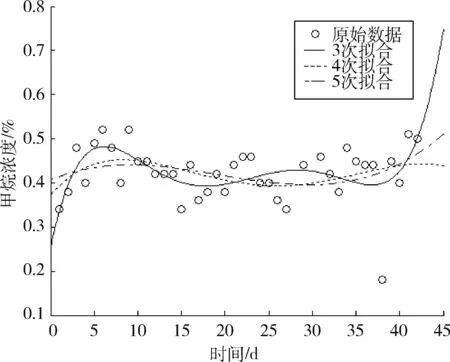
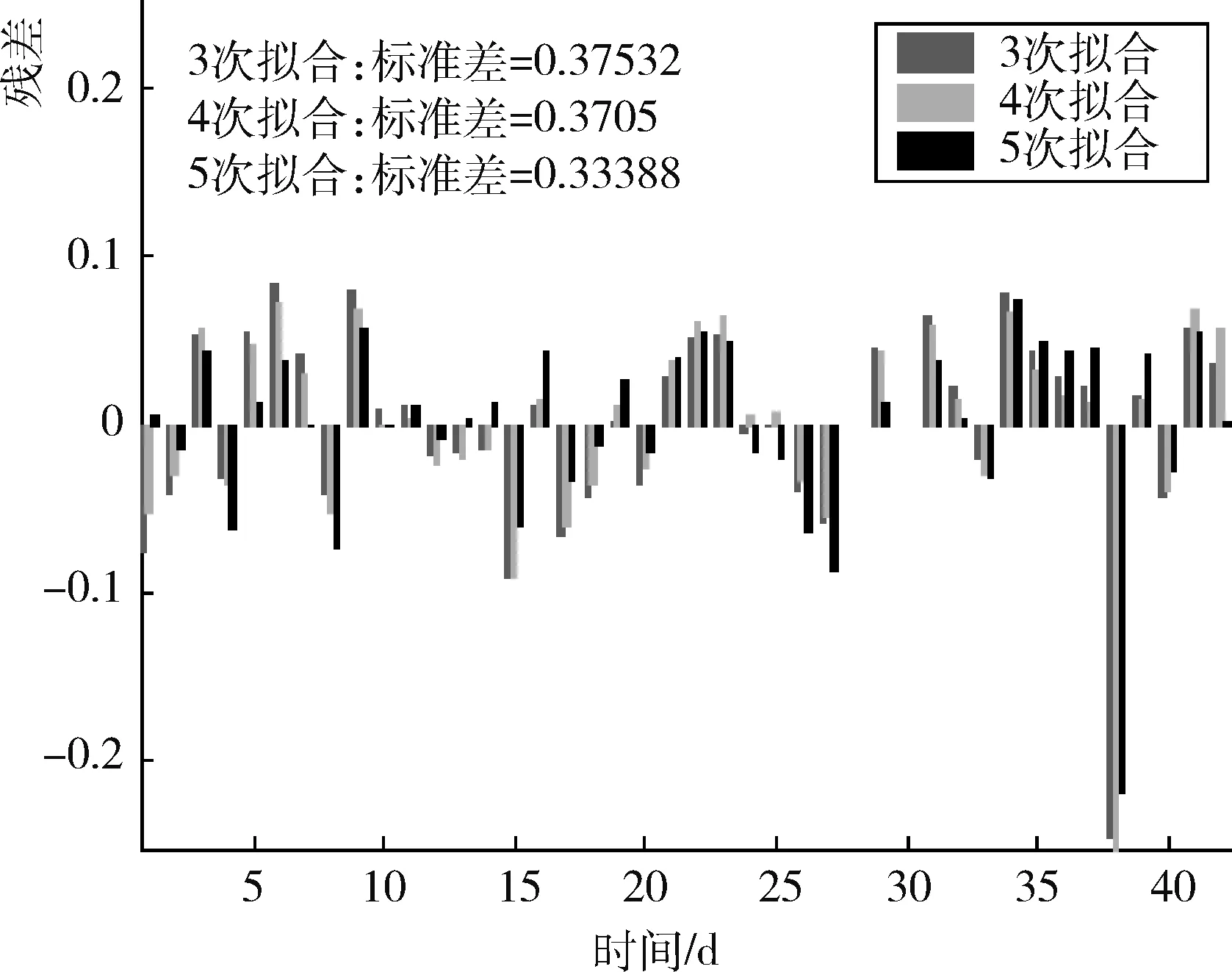
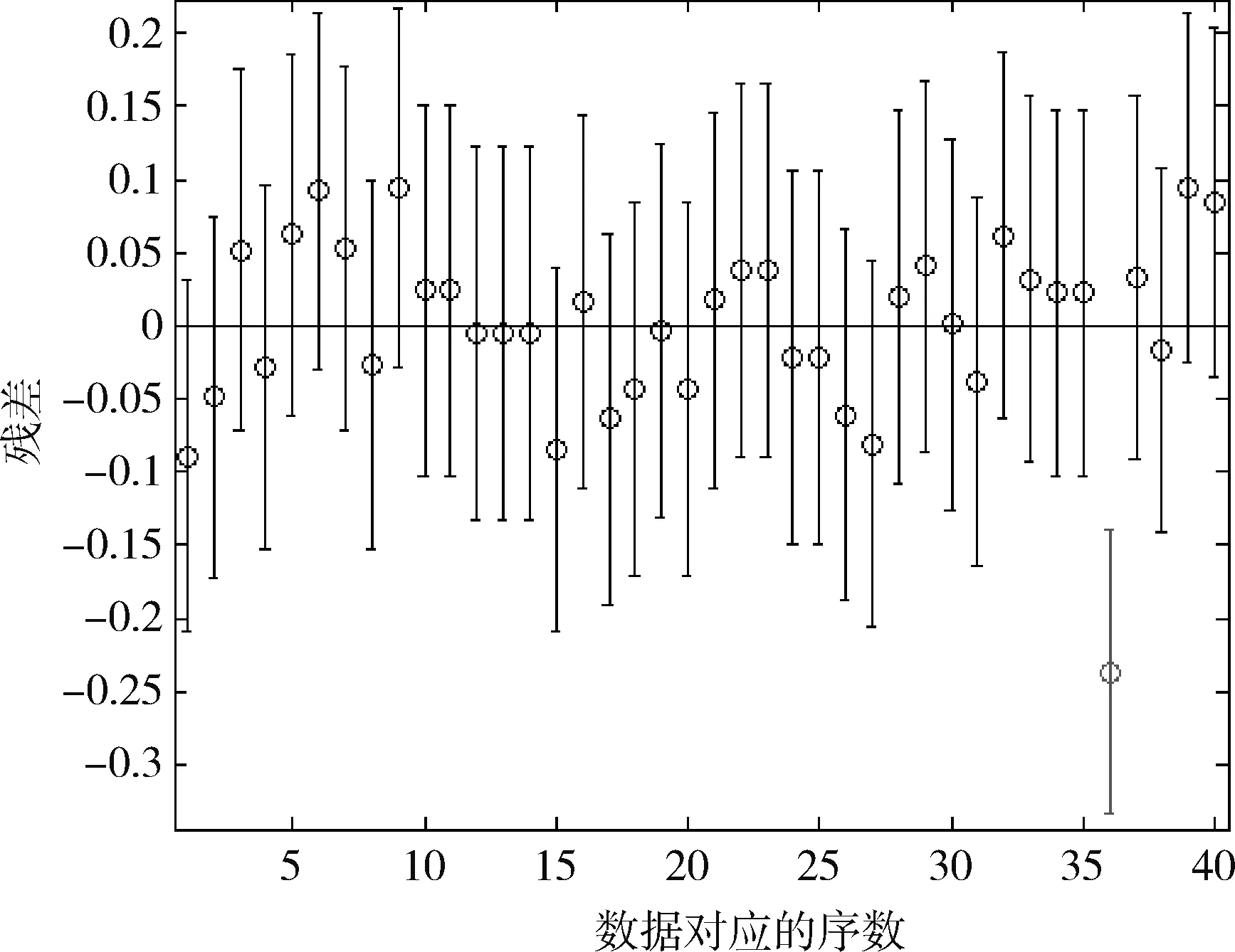
y=φ(x)=a0+a1x+a2x2+…+amxm(m

其中，a0，a1，…，am为待定系数，使其“最好”地拟合这组数据。“最好”的标准是：使得φ(x)在xi的偏差

的平方和

达到最小。

拟合曲线y=φ(x)通常不过点(xi,yi)。把(xi,yi)代入y=φ(x)，便得到以a0,a1,…,am为未知量的矛盾方程组，写为矩阵形式为

Ax=b

其中

那么以上矛盾方程的最小二乘解，也就是正则方程组ATAx=ATb的解，其中AT是矩阵A的转置。

由此方程组得到的唯一解代入拟合多项式y=φ(x)，即得所求的拟合曲线。可利用上隅角处n组气体观测数据(xi,yi) (i=1, 2, ...,n)，xi代表时间，yi代表某种气体的浓度，通过最小二乘拟合得出气体随时间的变化关系式y=φ(x)。

1.2 气体相关性分析

为了分析各种指标气体浓度之间的相关关系，可引入相关系数进行分析。由概率论可知[4]，两个随机变量的相关系数ρX，Y定义为：

式中：X代表某种气体的浓度；Y代表另一种气体的浓度；Cov(X，Y)为随机变量X和Y的协方差；D(X)、D(Y)分别为随机变量X、Y的方差。相关系数ρX，Y的取值范围为[-1，1]，ρX，Y的绝对值越大，说明随机变量X和Y的相关性越好，反之越差。当ρX，Y为负值时，说明随机变量X和Y的的变化方向相反，反之变化方向相同。

2 工程实例应用

2.1 拟合数据选取

为了分析实测工作面上隅角的瓦斯浓度，按照上述方法，选取2009年11月18日到2010年1月4日观测的瓦斯数据40组进行分析，观测数据如表1所示。

2.2 最小二乘法多项式拟合

对上隅角40组CH4气体数据，利用MATLAB中的polytool工具进行拟合，可以得到CH4浓度的大致分布，如图1所示。其中，横坐标代表第几天测量的数据，d；纵坐标代表CH4浓度，%。

从图1中可以看出，中间的实线能大致反映观测数据的变化规律，用polytool函数的目的是便于选取拟合函数模型。选用4次多项式进行拟合。在MATLAB中利用命令[P, S]=polyfit(x, y, 4)得出P值，这个值就是拟合多项式的系数，由y=poly2str(P, ‘x’)值得到拟合多项式为[5]：

y=(-0.06306x4+ 6.4603x3-211.16x2+ 2315.5x + 37170)×10-5

拟合后的图形及其残差如图2所示。从图2中发现，第36天观测的数据残差很大，这是因为那天工作面处于停采状态，测得的数据不能代表正常开采时上隅角瓦斯的浓度。

表1 瓦斯观测数据

3 曲线拟合分析

3.1 拟合方法的分析

理论上，提高多项式的次数可以提高拟合的精度。实验中有40组数据，最大可进行39次多项式拟合。高次多项式拟合确实使得曲线经过大部分的已知试验点，但曲线两端精度很差，不能很好的反映气体的变化规律。即高次多项式拟合的效果并不理想，如图3所示。从图4中我们可以看出，3、4、5次多项式拟合的标准差分别是0.37532、0.3705、0.33388，4次拟合优于3次拟合。高次多项式会产生Runge现象[6]，除非已知数据来自高次多项式，否则多项式拟合的次数一般不超过6次。图3中表明5次拟合效果并不理想，因此，4次拟合较合适。

3.2 拟合效果分析

图5所示为利用MATLAB中的regress和rcoplot函数得到的残差及其置信区间。从图5上可以看出，39组数据的残差都在置信区间里。拟合效果比较理想，所以拟合曲线成立。如果想更精确的去分析数据，可以通过判断残差剔除不理想的数据后多次拟合。

3.3 拟合结果分析

从图2看出，CH4的浓度在一定的范围内波动，这是由工作面开采条件决定的。工作面的风量和工作面的开采进度是不断变化的，造成采空区漏风的不同和工作面瓦斯释放速度的不同，使得CH4在工作面上隅角积聚的浓度发生变化波动。

图1 CH4浓度的大致分布

图2 拟合图形及其残差分布

图3 3、4、5次多项式拟合对比

图4 3、4、5次多项式拟合残差分布

图5 残差及其置信区间

3.4 气体的相关性分析

为了更好的分析工作面上隅角瓦斯的变化规律，以及考虑上隅角瓦斯的来源，本文引入相关系数来分析上隅角和其他气体的相关性。利用表1中的数据，在MATLAB中利用函数r=corrcoef(x，y)计算出上隅角瓦斯气体与工作面的瓦斯气体的相关系数r为

上隅角瓦斯气体与工作面的瓦斯气体的相关系数为0.441。说明上隅角瓦斯的来源只有一小半来自于工作面采煤释放的瓦斯，而一多半来自于采空区漏风带出的瓦斯。因此，该工作面的漏风是比较严重的。漏风把采空区的瓦斯带出，一部分停留在上隅角，造成上隅角的瓦斯浓度高于其他地方的瓦斯浓度。因此，为了控制采空区瓦斯被大量带到工作面，应控制采空区漏风量。

从整体来说，上隅角的瓦斯浓度还没有达到瓦斯积聚的浓度。这主要和该工作面的通风方式有关。该工作面采用回风尾巷法排放瓦斯，使得大量瓦斯从尾巷排除，上隅角不容易瓦斯积聚。

4 结论

本文利用MATLAB，基于最小二乘法对实测工作面上隅角的CH4浓度进行了拟合分析。结果显示，该工作面上隅角CH4浓度在正常开采时，CH4浓度符合4次多项式分布。根据矿上实际条件和相关性分析结果，得出工作面上隅角的瓦斯一小半来自于工作面，一多半来自于采空区漏风携带的瓦斯。由此判断出采空区的漏风情况有利于控制上隅角瓦斯的积聚。最小二乘法提供了一种分析数据的方法，可以在煤矿数据分析中加以推广。

[1] 王德明. 矿井通风与安全[M]. 徐州: 中国矿业大学出版社, 2007: 258-259.

[2] 余明高, 常绪华, 贾海林, 等. 基于最小二乘法的高抽巷CO浓度变化规律分析[J]. 防灾减灾工程学报, 2010, 30(2): 190-195.

[3] 黄永安, 李文成, 高小科. MATLAB7.0/Simulink6.0应用实例仿真与高效算法开发[M]. 北京：清华大学出版社, 2008.

[4] 高雷阜, 李伟. 新编概率论与数理统计[M]. 沈阳：东北大学出版社, 2000.

[5] 苏金明, 阮沈勇. MATLAB实用教程[M]. 北京：电子工业出版社, 2005.

[6] 林永. 高次插值Runge现象的可视化教学初探[J]. 宿州学院学报, 2008, 23(5): 147-149.