考虑井筒变质量流动的砾石充填水平井产能预测

李明忠，李彦超，王卫阳，姚志良，王一平，孟维龙

(1.中国石油大学 石油工程学院，山东青岛 266555;2.中国石油冀东油田分公司陆上作业区，河北唐山 063200)

考虑井筒变质量流动的砾石充填水平井产能预测

李明忠1，李彦超1，王卫阳1，姚志良1，王一平1，孟维龙2

(1.中国石油大学 石油工程学院，山东青岛 266555;2.中国石油冀东油田分公司陆上作业区，河北唐山 063200)

应用质量守恒和动量守恒原理推导砾石充填水平井井筒内变质量流动压降方程，并采用拟三维思想，将地层内流体在三维空间的流动分为水平面内的向垂直裂缝流和近井区域垂直平面内的径向流，建立油藏渗流模型。提出将井筒变质量流与油藏渗流耦合的数学模型及求解方法。结果表明：利用该模型计算的水平井产能与实测结果平均误差仅为3.79%，沿井筒流量分布计算值与生产测井值基本一致;越靠近水平井跟端，井筒内流体流速越大，加速度损失和摩擦损失越大，压力下降越明显;随着砾石充填层渗透率增加，产量先急剧增加，后趋于平稳，合理选择砾石充填层渗透率对提高水平井产能有重要意义。

水平井;井筒变质量流动;砾石充填;产能预测;耦合模型

水平井技术作为开发稠油、低渗、古潜山等特种油气藏的技术近年来得到了迅速发展，国外研究者Joshi等［1-2］主要利用无限导流假设，对水平井的天然产能进行研究。20世纪80年代以后，国内外一些学者在砾石充填防砂技术方面开展了大量的研究工作，部分学者在Joshi公式的基础上引入钻井和完井表皮系数，得到砾石充填等不同完井方式下水平井的产能预测公式［3-6］，以上研究均未考虑井筒变质量流动对产能的影响。实际生产中随着地层流体的不断流入，水平井筒中形成了流量渐增的变质量流动，此时如果忽略水平段内压降势必对计算结果产生较大影响［7］。20世纪90年代末开始，许多学者在有限导流的基础上对水平井筒内的流动规律进行了研究［8-12］，但针对砾石充填防砂水平井产能的研究较少。笔者在综合研究裸眼砾石充填水平井油藏渗流和井筒变质量流动的基础上，建立该类水平井油藏渗流与井筒变质量流动耦合模型，运用四阶Runge-Kutta数值方法对模型进行求解，准确计算该类水平井的产能及沿井筒的压力、流量分布。

1 油藏渗流与井筒变质量流动耦合模型

水平井生产过程中地层流体的径向入流改变了水平井井筒内的主流边界层，因此井筒内的流动规律不同于常规管流;同时，井筒内流体流量逐渐增加，须考虑加速度损失。井筒内的压力分布影响了油藏流体径向入流量，油藏入流量又会影响管内压力分布(图1)。因此，综合考虑油藏渗流与井筒变质量流动的耦合才能准确预测水平井的产能。

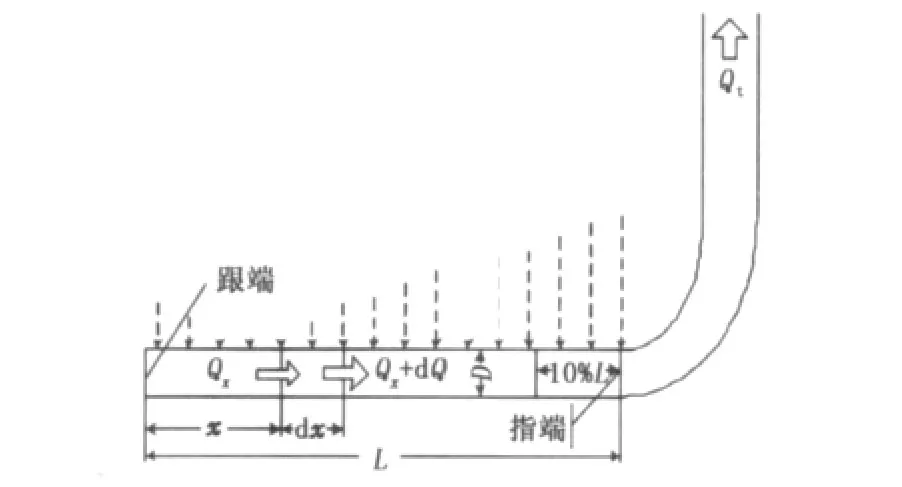
图1 水平井井筒变质量流动示意图Fig.1 Schematic diagram of variable mass flow in horizontal wellbore

1.1 井筒变质量流动压降计算模型

取任一水平井井筒微元段(图2)，管内流体为单相不可压缩流体，设井筒长为L，直径为D，由质量守恒原理得

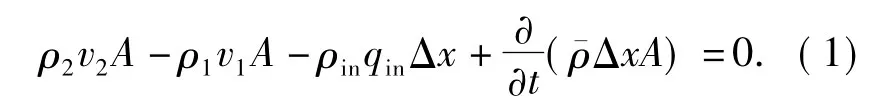
式中，A为井筒微元段截面积，m2;Δx为井筒微元段长度，m。ρin为流体密度，kg/m3;¯ρ为微元段流体平均密度，kg/m3;ρ1和ρ2分别为井筒微元段截面1、2处流体的密度，kg/m3;v1和v2分别为在井筒微元段截面1、2处的流速，m/s;qin为油藏向井筒微元段的入流量，m3/(s·m)。

当Δx→0时，式(1)可以简化为式中，x为井筒内任意一点到井筒指端的距离，m;ρ为井筒内任意点的流体密度，kg/m3;v为流体在井筒内任意点的流速，m/s。

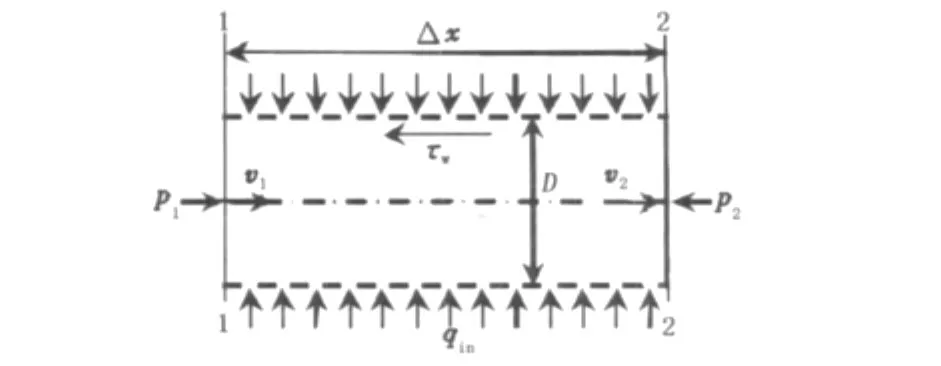
图2 水平井井筒微元段Fig.2 Volumetric control element of horizontal wellbore

假设油藏流体向井筒的流动为径向流，流动方向与井筒轴向垂直，对图2微元段，由动量守恒原理得

式中，θ为井筒微元段与水平方向的夹角，rad;τw为井筒微元段内壁剪切应力，N/m2;p1和p2分别为井筒微元段截面1、2处的压力，MPa。

当Δx→0时，式(3)可化简为

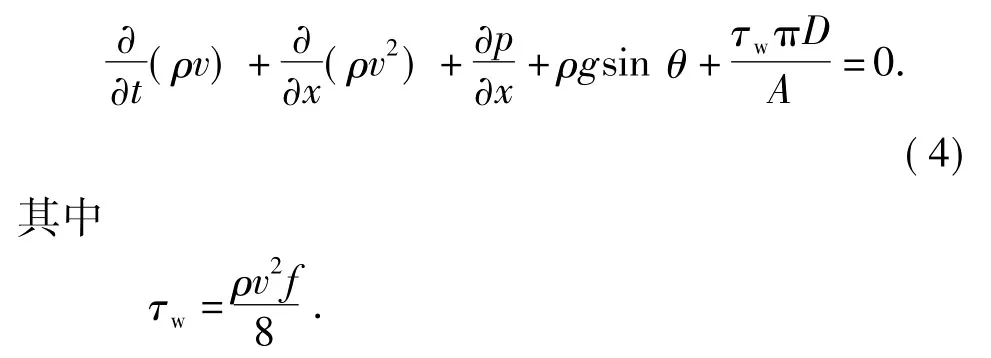
式中，f为井筒摩擦系数;p为井筒内任意一点的压力，MPa。

当井筒内为单相不可压缩流体稳态流动时，式(2)和式(4)可简化为

筛管内主流边界层受到油藏流体径向入流的影响，其流动规律不同于常规管流，因此该类管中摩擦系数的计算需要考虑油藏流体径向入流的影响［11］：式中，fo为常规管紊流摩擦系数;ε为常规管璧面粗糙度，m。

1.2 地层渗流模型

对于裸眼砾石充填防砂水平井开发的疏松砂岩油藏，若忽略油水黏度差或油井的含水率较低，则流体的流动可以看作单相流，应用拟三维思想，三维空间中流体流动分为两部分：流体由油藏供给边缘向水平井近井地带的流动，即水平地层内流体由油藏供给边缘向一条垂直裂缝的流动;流体由水平井近井区向井筒的径向流动，即垂直面内的径向流动［4］。

1.2.1 水平面内向垂直裂缝的流动

油藏内流体向垂直裂缝流动的流动方程为

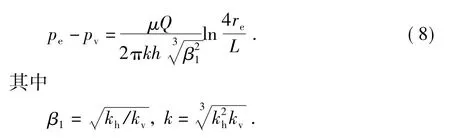
式中，re为泄油半径，m;Q为水平井产量，m3/d;pe和pv分别为油藏边缘、近井区域外缘压力，MPa;kh和kv分别为储层水平、垂直渗透率，μm2;μ为原油黏度，mPa·s;h为油藏厚度，m。

1.2.2 垂直平面内的径向流动

垂直平面内的径向流动可以看作3个区域流动的组合：Ⅰ区是由外部流动区域向圆形等压区的流动;Ⅱ区是由圆形等压区到砾石充填层外缘的流动;Ⅲ区是砾石充填层外缘到井筒的流动。

流动Ⅰ区的产量－压差公式为

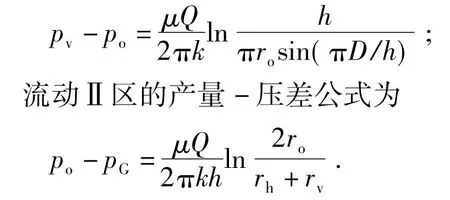
式中，pG和po分别为砾石充填层外缘和圆形等压区的压力，MPa;rh和rv分别为椭圆区域长、短轴半径，m。

流动Ⅰ区和Ⅱ区地层受到钻井污染，污染表皮系数Shd的计算式为

式中，kd为钻井损害区的渗透率，μm2;rd为钻井损害半径(井眼半径+损害厚度)，m;rw为井筒半径，m;β为地层各向异性系数。

水平井钻井污染区域的流动方程为

1.3 井筒变质量流动与渗流耦合模型及其求解

假设油藏储层均质各向异性，油藏边界为定压边界，单相不可压缩流体，油藏中水平方向的压力梯度较垂向的压力梯度可忽略不计，则沿水平井比采油指数Jsp(Jsp=Js/L)为常数［13］。油藏向单位长度井筒的入流量qin为

式中，vt为井筒指端流速，m/s;pt为井筒指端压力，MPa。

应用四阶Runge-Kutta法对油藏渗流与井筒变质量流耦合模型进行求解，在Matlab中可以应用自适应步长算法进行求解。求解过程中，用户可以定义合理的容差来检测计算精度、调整步长Δx，该算法既提高了运算速度又有较高的计算精度。

2 模型验证及计算结果分析

应用某油藏砾石充填防砂水平井数据(表1)进行模型的验证及计算结果分析，计算结果见表2。本文中计算的砾石充填水平井产能与试井实测结果基本一致，较Joshi公式有更精确的计算结果，与试井实测结果平均误差仅为3.79%，这说明井筒变质量流动对水平井产能产生较大影响。

表1 砾石充填水平井基本数据Table 1 Basic data of gravel-packed horizontal well

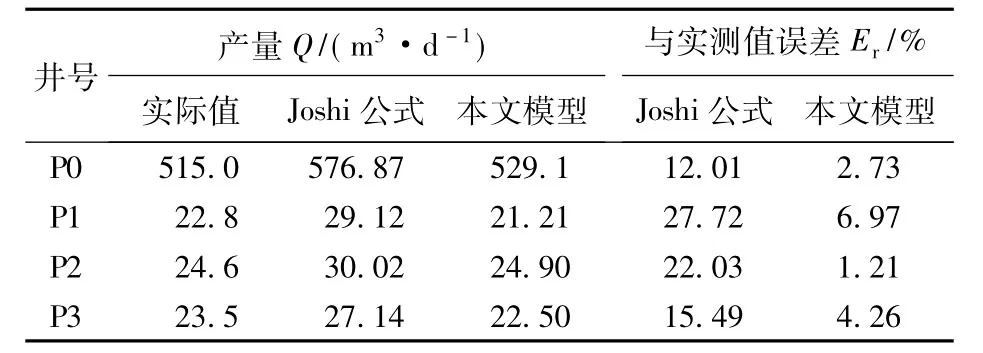
表2 砾石充填水平井计算结果Table 2 Calculation result of gravel-packed horizontal well

以P0井为例，计算了沿井筒的压力和流量分布(图3)。由图3可以看出：计算所得沿水平井井筒流量分布与生产测井资料所得流量分布基本一致;从井筒指端到跟端压力逐渐降低，越接近跟端，压力下降越快，以井筒跟端为起点，取20%的井筒长度，压力下降占全井总压降的39.3%，主要原因是井筒跟端压力最低，越接近井筒跟端，油藏与井筒压差越大，油藏流体向井筒入流流速越大，井筒加速度损失和摩擦损失越大。从产量沿水平段长度分布(图4)可以看出，生产时水平井筒中的流动是流量渐增的变质量流动，越接近井筒跟端，单位长度井筒流量越大。

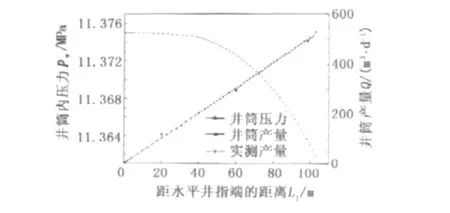
图3 沿水平井井筒压力和产量分布曲线Fig.3 Pressure and productivity distribution along horizontal wellbore

不同砾石层渗透率下该类水平井产能计算结果如图5所示。随着砾石层渗透率增加，产量先急剧增加，后趋于平稳。因此，在现场应用该类防砂水平井开发时，合理选择充填砾石层渗透率对提高水平井产能有重要意义。

3 结论

(1)考虑井筒变质量流动影响建立的裸眼砾石充填水平井井筒变质量流与油藏渗流耦合模型计算产量平均误差仅为3.79%。

(2)生产时水平井筒中的流动是流量渐增的变质量流动。随着井筒的加速度损失和摩擦损失增加，靠近指端，压力下降较慢，越接近跟端，压降下降越快。

(3)随着充填砾石层渗透率增加，产量先急剧增加，后趋于平稳，合理选择充填砾石层渗透率对于提高该类防砂水平井产能有重要意义。

［1］GIGER F M，REISS L II，JOURDAN A P.The reservoir engineering aspect of horizontal drilling［R］.SPE 13024，1984.

［2］JOSHI S D.Augmentation of well productivity using slant and horizontal wells［R］.SPE 15375，1986.

［3］李爱芬，姚军，寇永强.砾石充填防砂井产能预测方法［J］.石油勘探与开发，2004，31(1)：103-105.

LI Ai-fen，YAO Jun，KOU Yong-qiang.A method of calculating productivity for gravel packed well［J］.Petroleum Exploration and Development，2004，31(1)：103-105.

［4］ 刘月田.各向异性油藏水平井渗流和产能分析［J］.石油大学学报：自然科学版，2002，26(4)：40-47.

IIU Yue-tian.Analysis on seepage flow and productivity of a horizontal well in an anisotropic reservoir［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2002，26(4)：40-47.

［5］董长银，武龙，王爱萍，等.基于平衡流速的水平井砾石充填α波砂床平衡高度预测与试验［J］.中国石油大学学报：自然科学版，2009，33(5)：80-88.

DONG Chang-yin，WU Long，WANG Ai-ping，et al.Prediction and experiment for wave equilibrium sand bed height in horizontal well gravel-packing based on equilibrium velocity［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(5)：80-88.

［6］董长银，武龙，王爱萍，等.水平井及大斜度井砾石充填过程试验［J］.中国石油大学学报：自然科学版，2010，34(2)：74-82.

DONG Chang-yin，WU Long，WANG Ai-ping，et al.Experimental simulation of gravel-packing in horizontal and highly deviated well［J］.Journal of China University of Petroleum(Edition of Natural Science)，2010，34(2)：74-82.

［7］张琪，周生田，吴宁，等.水平井气液两相变质量流的流动规律研究［J］.石油大学学报：自然科学版，2002，36(6)：46-50.

ZHANG Qi，ZHOU Sheng-tian，WU Ning，et al.Laws of gas-liquid two-phase varible mass flow in horizontal wellbore［J］.Journal of the University of Petroleum，China(E-dition of Natural Science)，2002，36(6)：46-50.

［8］YUAN H J.Effect of perforation density on single-phase liquid flow behavior in horizontal wells［R］.SPE 57395，1999.

［9］李明忠.井筒变质量流与油层中渗流耦合的水平井产能计算方法研究［D］.北京：中国矿业大学力学与建筑工程学院，2003.

LI Ming-zhong.Research on method to calculate produtivity of horizontal wells with variable mass flow in well bore coupling with seepage in reservoir［D］.Beijing：School of Mechanics＆ Civil Engineering，China University of Mining ＆ Technology，2003.

［10］汪志明，赵天奉，徐立.射孔完井水平井筒变质量湍流压降规律研究［J］.石油大学学报：自然科学版，2003，27(1)：41-44.

WANG Zhi-ming，ZHAO Tian-feng，XU Li.Pressure drop of variable mass flow in horizontal perforated well bore［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2003，27(1)：41-44.

［11］王小秋，汪志明，魏建光.井筒与油藏藕合条件下水平井变质量流动规律研究［J］.水动力学研究与进展，2005，20(3)：311-326.

WANG Xiao-qiu，WANG Zhi-ming，WEI Jian-guang.Investigation of variable mass flow in horizontal well with perforation completion coupling reservoir［J］.Journal of Hydrodynamics，2005，20(3)：311-326.

［12］黄世军，程林松，赵凤兰，等.考虑多段流动耦合的鱼骨刺井产能评价模型［J］.中国石油大学学报：自然科学版，2010，34(2)：83-88.

HUANG Shi-jun，CHENG Lin-song，ZHAO Feng-lan，et al.Production evaluation model of fishbone well considering coupling among multi-segments flow［J］.Journal of China University of Petroleum(Edition of Natural Science)，2010，34(2)：83-88.

［13］刘慈群.水平井流量公式［J］.石油钻采工艺，1991，13(1)：32-32，40.

LIU Ci-qun.Horizontal well flow equation［J］.Oil Drilling ＆ Production Technolgy，1991，13(1)：32-32，40.

Productivity prediction for gravel-packed horizontal well considering variable mass flow in wellbore

LI Ming-zhong1，LI Yan-chao1，WANG Wei-yang1，YAO Zhi-liang1，WANG Yi-ping1，MENG Wei-long2
(1.College of Petroleum Engineering in China University of Petroleum，Qingdao 266555，China;2.Land Oil Production Plant of Jidong Oilfield Company，PetroChina，Tangshan 063200，China)

According to the principle of mass and momentum conservation theorem，the pressure drop equations of variable mass flow in the gravel-packed horizontal well were derived.The fluid flow in 3-D space was divided into flowing towards vertical fracture in the horizontal plane and radial flowing in the vertical plane near the wellbore.Using pseudo-three dimensional idea，the reservoir seepage model was developed.The model coupling seepage in reservoir with variable mass flow in wellbore was established and the solving method was given.The results show that the calculated results of well production by this model have high precision and the average error with field data was only 3.79%.The calculated flow rate along wellbore is consistent with the logging derived flow rate.The smaller the distance from root end of wellbore，the greater the fluid velocity in wellbore，the acceleration loss，the friction loss and pressure drop.With the permeability of gravel-packed layer increasing，the production increases sharply，after stabilizing，so a reasonable choice for permeability of gravel-packed layer is important to improve horizontal well productivity.

horizontal well;variable mass flow in wellbore;gravel-packing;productivity prediction;coupling model

TE 358.2

A

10.3969/j.issn.1673-5005.2011.03.018

1673-5005(2011)03-0089-05

2010－07－10

李明忠(1963－)，男(汉族)，山东利津人，教授，博士，博士生导师，从事采油工程、井筒多相流动理论研究。

(编辑 李志芬)