高职院校学生综合素质的多属性评价方法
2011-01-20黄会明
黄会明
(浙江机电职业技术学院电气电子工程学院,浙江杭州310053)
大学生综合素质测评是高等院校学籍管理中一项重要而复杂的工作,是提高教育管理水平,激励、引导大学生德、智、体、美等方面全面发展重要措施。学生管理部门通过综合素质测评,掌握大学生在校期间德、智、体等方面的表现情况,测评结果常作为学生评优评奖、推荐就业的主要依据,同时也是学生推优入党的一个重要依据[1]。随着我国高等教育改革的不断深入,综合素质测评工作不仅可激励学生培养广泛的兴趣爱好、提高专业学习的积极性及科技创新意识,而且在为社会、企业培养与选拔高素质人才等方面也发挥着越来越重要的作用。
目前,各高校在进行综合素质测评时,大多将考试成绩作为衡量大学生综合素质和能力的主要评价标准,常采用量化计算的方法,即将德育、智育、体育等各项素质全部量化,然后计算得出各学生的综合素质总分或加权平均分,再根据分值的高低来确定综合素质的优劣。这种简单的量化评价方法易受到主、客观因素的影响,难免出现不同程度的失真偏差,使大学生综合素质水平难以得到准确评价。由于综合素质测评是属于多属性综合评价的范畴,现尝试将TOPSIS和秩和比方法相结合,探索出综合素质评价的科学化途径。
1 综合素质评价体系与数据来源
1.1 综合素质评价体系
大学生的综合素质是一个庞大而复杂的系统,反映其水平、影响其变化的因素比较多,如何建立科学的评估体系是各大学学生工作者多年来一直在探索的问题。为了客观、准确、完整地对学生的综合素质做出评价,必须要筛选出能够全方位、多角度反映学生综合素质的评价指标,反映其多指标评价的层次结构[2]。
参照相关综合素质评价文献[3][4][5],通过发放调查表,并征求专家意见,根据评价指标体系全面、科学、可比性及可操作性的要求,结合高职教育的特点,最后建立了以思想政治素质为核心的,以知识素质为基础的,以能力素质为关键的高职学生综合素质评价指标体系。该指标体系主要由思想政治素质、理论素质、实践素质、体育素质等4个方面共13项指标组成,详见表1。
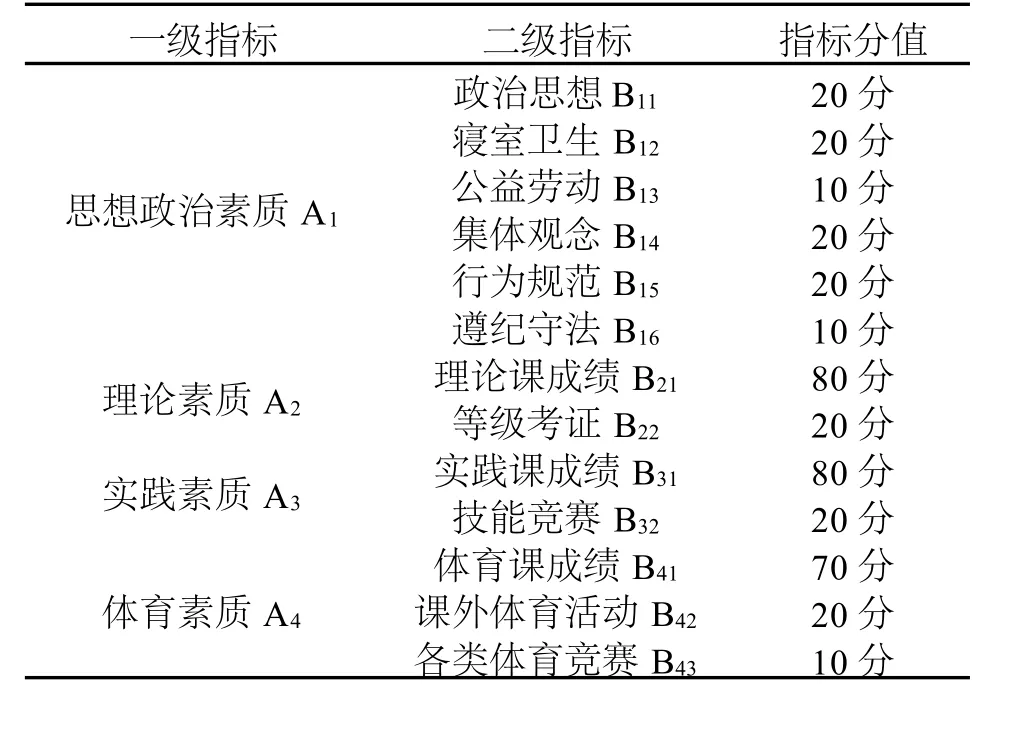
表1 大学生综合素质评价指标体系
1.2 数据来源
本文以某高职院校08级汽车检测与维修专业学生为研究对象,综合素质的测评数据采自二年级第一学期。理论课程有:微机原理、专业英语、汽车构造、汽车传感器原理等;实践课程有:微机原理实训、发动机构造实训、汽车底盘构造实训等。同时,结合学生的等级考证、各级各类技能竞赛及体育比赛等,汇总后得出学生的理论素质、实践素质及体育素质得分。思想政治素质得分综合学生各方面的表现,采用记实量化得出。现选取学号为 XS1至XS13的学生的各项素质成绩,汇总后见表2。

表2 综合素质计算数据表
2 应用 TOPSIS法评价
2.1 TOPSIS法理论与方法
TOPSIS法(Technique for order preference by similarity to ideal solution),即逼近理想解排序法,是一种多属性决策方法。TOPSIS法的基本思想是:基于归一化后的原始数据矩阵,找出有限方案中的最优方案和最劣方案(分别用最优向量和最劣向量表示),然后分别计算各评价对象与最优方案和最劣方案的距离,获得该评价对象与最优方案的相对接近程度,以此作为评价优劣的依据[5]。计算步骤如下:
(1)决策矩阵的构建。设某一多目标决策问题有p个评价指标,同时有n个评价单元,得到各评价对象在某指标下的取值 xij,X=(xij)n×p即为决策矩阵。
(2)计算加权标准化决策矩阵。为了反映各指标的相对重要程度,排除由于各项指标单位不同所带来的影响,避免不合理现象的发生,需要对决策矩阵作加权标准化处理。令

式中:wj为第 j个指标的权重系数,文中由AHP计算得到。
(3)参考相关文献[6],计算各指标与正理想解、负理想解的距离,以及相对接近度。然后根据值对各评价对象进行排序,评价对象的值越大,表示越接近最优目标。
2.2 指标权重确定
指标的权重反映了该指标在整体中的相对重要程度,确定指标权重的常用方法主要有:层次分析法(AHP)、达尔菲法(Delphi)、主成分分析法、灰关联法、熵值法和均方差法等。
本文借鉴AHP确定指标重要性权重的思想,并结合高职院校人才培养特点,通过咨询六位教育专家,采用群体决策的方法确定指标权重[7],最终确定的权重见表3。

表3 学生综合素质各指标权重
2.3 TOPSIS法评价结果
现借助DPS软件[8],采用 TOPSIS法对表2中各学生的综合素质进行评价。分析时,各指标的权重参照表3,最终得到的结果见表4。

表4 指标值与最优值的相对接近程度及名次
根据Ci值的大小,可以得到各位学生综合素质的排序。由表4可知,XS1学生的Ci值最大,表明其综合素质相对最优,其次为XS5学生,随后依次为 XS7、XS2、XS4、XS6、XS3、XS8、XS10、XS11、XS09、XS12,而XS13的综合素质相对最劣。
3 应用秩和比法评价
秩和比法(Rank Sum Ratio,简称为RSR)是我国统计学家田凤调教授创造的一种统计学方法,它是集中了古典的参数统计和近代的非参数统计各自优势的一套崭新的统计分析方法。它把意义不同的各评价指标实测值转化为秩次,然后加权求和,再根据秩和比大小进行排序,实现对不同评价对象的测评。秩和比评价时,算得的RSR值越大,表明评价对象越优,为此应先区分原指标是属于“高优”还是“低优”[9]。本例中,综合素质测评所用的各指标都属“高优”指标。
(1)排秩次R。根据编秩方法,高优指标的最大指标值的秩次最高,最小指标值的秩次为1,若指标值相同,则为平均秩次。最终得到的综合素质各指标秩次,见表5。

表5 综合素质各指标的秩次与秩和比
根据秩和比评价原则,由表5可知,学生XS1的RSR值最大,学生XS5的RSR值次之,表明学生XS1的综合素质相对最优,学生 XS5次之;而XS13学生的RSR值最小,表明其综合素质相对最差。其中,学生XS2、XS3、XS4的RSR值相同,参考TOPSIS法的综合评价结果,确定综合素质的优劣排序为学生XS2、XS4、XS3。
4 结果与讨论
通过表4、表5的综合素质评价结果比较发现,两种方法的排序结果基本一致,其原因是由于所用的公式和原理不一样所导致的。综合考虑不同方法评价结果,可弥补单一评价方法的不足,使评价结果与实际情况相吻合,使评价结果更具准确性、客观性、实用性。根据不同评价结果的区分度、公众接受度、主客观结合程度、拟合度等,可对不同方法的结果进行加权综合,得出最终的评价结果。
现拟采用乘法合成法,对TOPSIS和RSR方法的排序结果进行综合,具体赋权公式为:
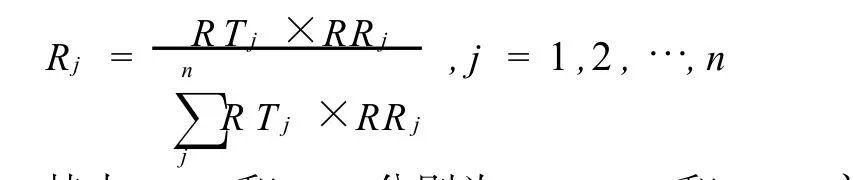
其中,RTj和RRj分别为TOPSIS和RSR方法的排序名次。最终得到的评价结果,见表6。

表6 学生综合素质排序
另外,综合评价的结果是否合适,还取决于选择的指标是否具有代表性,权重系数是否合理,统计方法是否科学。因此,在进行综合素质评价时,应根据少而精的原则,择优选取有代表性、确定性、可比性、可操作的指标,并运用合理的方法来确定权重,量化因素之间的关系,以期达到较符合客观实际的评价结果。
[1]黄会明.多指标综合评价法在大学生综合素质评价中的应用[J].温州职业技术学院学报,2009(4):81-83.
[2]张 英,冯艳芳.基于模糊层次分析法的大学生综合素质评价[J].武汉理工大学学报(社会科学版),2007(5): 707-710.
[3]丁家彬.模糊综合评判法在大学生综合素质评判中的应用[J].唐山师范学院学报,2007(5):48-51.
[4]杨春华.模糊聚类分析在大学生综合素质评定中的应用[J].保山师专学报,2009(2):40-46.
[5]丁荣华,白丹莉,程 波.从综合素质方面对高校学生的综合评价研究 [J].科技通报,2001(6):30-34.
[6]黄会明,陈 宁,严小明,等.应用AHP与TOPSIS法评价高职学生综合素质[J].职业技术教育,2009(13):46-49.
[7]赵焕臣.层次分析法——一种简易的新决策方法[M].北京:科学出版社,1986:1-28.
[8]唐启义,冯明光.DPS数据处理系统—实验设计、统计分析及数据挖掘[M].北京:科学出版社,2007:1093-1097.
[9]田凤调.秩和比法及其应用[M].北京:中国统计出版社,1993:1-12.
