浅析Stirling公式的若干应用
2011-01-19刘丹丹
韩 诚 刘丹丹
(盐城师范学院 数学科学学院,江苏 盐城 224002)
1 利用Stirling公式证明Wallis公式
Wallis公式
它是关于圆周率的无穷乘积的公式,公式中只有阶乘运算,形式十分简单,但它是有理数过渡到无理数的一个非常重要的桥梁。而对于Wallis公式的证明,一般情况下,都用积分证明方法[3],证明过程比较复杂,本文利用Stirling公式证明Wallis公式,使其证明过程简单明了。
Wallis公式的证明:


2 Stirling公式在欧拉积分中的应用

定理1:对任意x>0存在θ(x)∈(0,1)使得
(1)
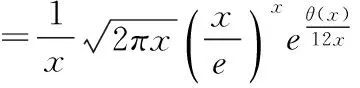
两边取对数得
(2)
因此只要证明公式(2)就可以了。
下面通过四个引理来证明公式(2)。
引理2:对任意x>0,满足不等式
引理3:对任意的自然数n,有
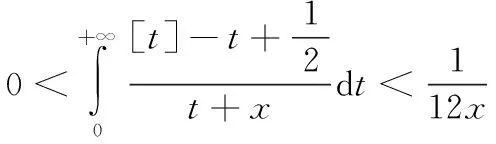
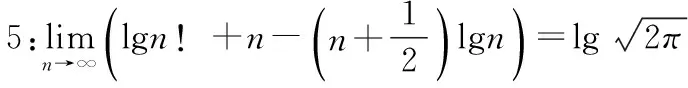
现在来证明(2)式。


(3)

又(3)式左端第一项当n→∞时的极限是lgΓ(x),在(3)式的两边让n→∞,即得
(4)

这即是要证明的(2)式,从而定理得证。
3 Stirling公式在微积分中的应用
在微积分中,经常会遇到含有n!的数列计算,并且有些数列计算是比较难的,因此可以借助Stirling公式来简化计算过程。
3.1 Stirling公式在数列极限中的应用
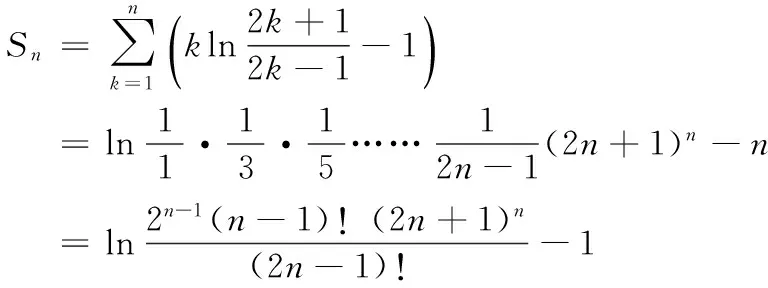
由Stirling公式得
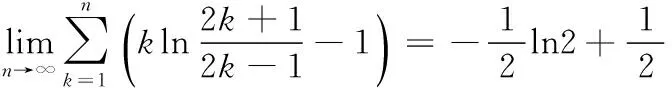
3.2 Stirling公式在乘积不等式中的应用

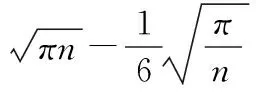


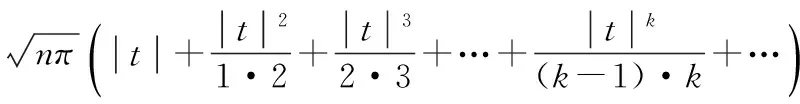
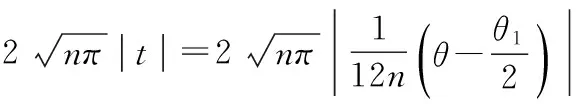
4 Stirling公式在概率统计中的应用

这样,就可以得到二项分布的概率近似值。
下表表示对一些二项分布的概率利用阶乘近似所得计算结果与按定义计算(或查表所得)值的比较[4]。
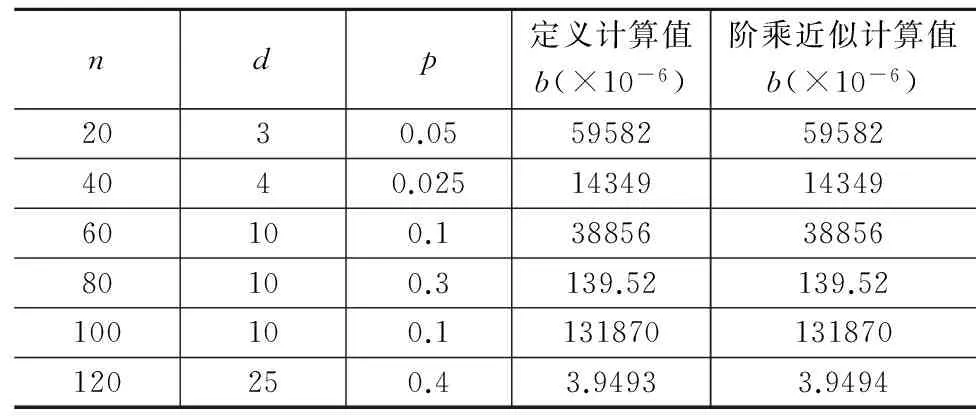
若干二项分布概率近似值
这种方法比较简单,并且计算结果精度较高。另外,计算者可以自行调整精度值,以满足实际问题的需要。
[1]刘会成.Stirling公式在一个乘积不等式中的应用[J].数学通报,2002,(10):46.
[2]江旭光.两类极限的求法[J].安徽教育学院学报,2000,(3):60.
[3]华东师范大学数学系.数学分析(上册):第3版[M].北京:高等教育出版社,2006:227.
[4]彭求实.Stirling公式的改进及二项分布概率的近似计算[J].哈尔滨商业大学学报:自然科学版,2006,(4):102~103.
